公式定义:
对测试样本 xx , 表示在 xx 数据集上的标记, 为 xx 的真实标记, 为训练集D上学得模型 ff 在 上的预测输出。以回归为例:
算法的期望预测:
f−(x)=ED[f(x;D)]f−(x)=ED[f(x;D)]
使用样本数相同的不同训练集产生的方差为:
var(x)=ED[(f(x;D)−f−(x))2]var(x)=ED[(f(x;D)−f−(x))2]
噪声为:
ϵ2=ED[(yD−y)2]ϵ2=ED[(yD−y)2]
期望输出与真实标记的差别称为偏差(bias),即
bias2(x)=(f−(x)−y)2bias2(x)=(f−(x)−y)2
关系:泛化误差可分解为偏差、方差和噪声之和
E(f;D)=bias2(x)+var(x)+ϵ2E(f;D)=bias2(x)+var(x)+ϵ2
偏差、方差、噪声的含义:
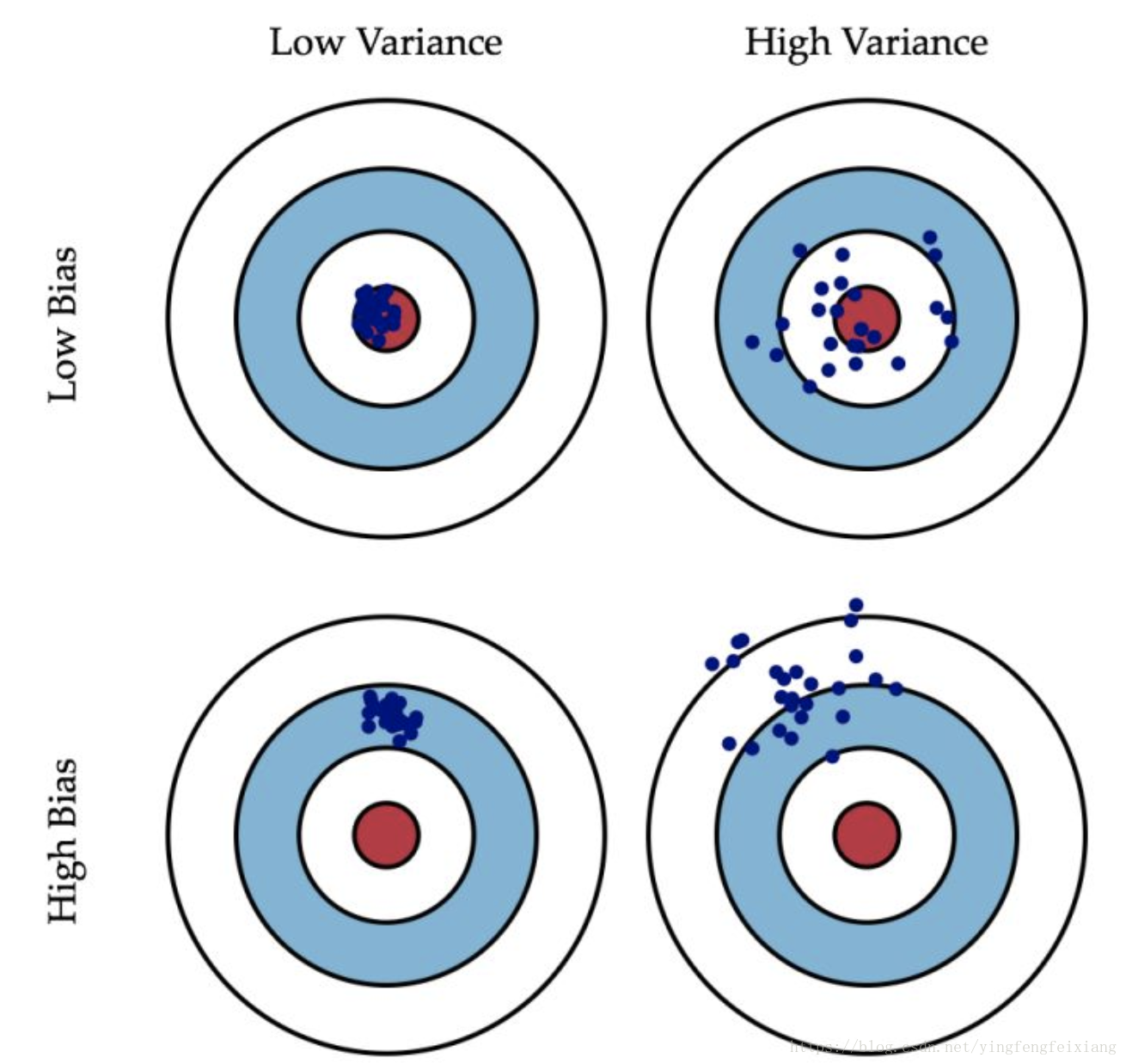
- 偏差:
度量了学习算法的期望预测与真实结果的偏离程度,即刻画了算法本身的拟合能力。偏差越大越偏离真实值。 - 方差:
度量了同样大小训练集的变动所导致的学习性能的变化,即刻画了数据扰动所造成的影响。反映了离散程度,预测值到期望值的距离;方差越大,数据分布越分散。也就可以理解为衡量模型的稳定性(鲁棒性)。 - 噪声:
表达了在当前任务上任何学习算法所能达到的期望泛华误差的下界,即刻画了学习问题本身的难度。
























 438
438

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








