Day02 数组part02

第二天：数组part02（有序数组的平方 ，长度最小的子数组 ，螺旋矩阵II ）

LC977有序数组的平方

1. 暴力解法：遍历循环数组每个元素，然后求平方，最后进行排序

• 时间复杂度：O（n+nlogn）

2. 双指针解法（未掌握）：

• 思想：
  • 数组本身就是有序的，只不过在平方的过程中可能存在负数平方成为最大数
  • 因此数组平方后的最大值就在数组的两端，不是最左边就是最右边
  • 定义一个新数组，k指向末尾位置用来表示平方最大值，双指针i和j分别指向0和nums.length-1
    • nums[i] * nums[i] < nums[j] * nums[j] 那么result[k–] = nums[j] * nums[j];
    • nums[i] * nums[i] >= nums[j] * nums[j] 那么result[k–] = nums[i] * nums[i];
  • 时间复杂度：O（n）

3. 代码：
   

LC209长度最小的子数组（未掌握）

1. 未掌握分析：连暴力解法都没了解过，陷入dp的思维漩涡中
2. 暴力解法：

• 维持两个for循环，其中第一个fori中的i定义为窗口的起始位置，第二个forj中的j定义为窗口的终止位置。
• 不断遍历得到所有的窗口情况，再去判断窗口sum>=target的情况
• 时间复杂度：O（n^2）

3. 双指针滑动窗口解法

• 滑动窗口介绍： 不断的调节子序列的起始位置和终止位置，从而得出我们要想的结果
• 使用一个for循环来完成上述操作：循环中的j定义为窗口的终止位置
  • 原因介绍：如果j是起始位置，那么跟暴力解法无异，仍然需要不断遍历得到终止位置
• 窗口起始位置的移动：根据当前子序列和大小的情况，不断调节子序列的起始位置
  • 当sum>=target：起始位置右移，缩小窗口大小
  • 当sum<target：不变，终止位置右移即可
  • 使用while循环来移动起始位置而不是if判断，因为if判断只能移动一次，但是却存在移动多次的情况
• 时间复杂度：O（n）

4. 代码：
   

LC59螺旋数组II（未掌握）

1. 二分法中的循环不变量思想：区间的定义就是不变量，在while寻找中每一次边界的处理都要坚持根据区间的定义来操作
2. 模拟顺时针画矩阵的过程

• 填充上行从左到右
• 填充右列从上到下
• 填充下行从右到左
• 填充左列从下到上
• 每一条边都需要遵循左闭右开的条件(左闭右开？是否熟悉，再联系循环不变量和数组=》二分法的思维)

3. 循环次数的定义：循环n/2次，，如果是奇数n，那么最后再判断一下，判断成功直接复制
4. 定义循环不变量：

• 从哪个位置开始判断：startx，starty
• 终止位置：offset

5. 顺时针过程：

• 上行左到右：i=startx，j从starty到n-offset：j = starty;j<n-offset;j++
• 右列上到下：j已经确定不变，i从starx到n-offset：i = startx;i<n-offset;i++
• 下行从右到左：i已经确定不变，j的初始值也已经确定，j从初始值到starty：;j>starty;j–
• 左列从下到上：j已经确定不变，i的初始值也已经确定，i从初始值到startx：;i>startx;i–

6. 不变量的循环迭代：startx++,starty++,offset++
7. 代码：
   

LC904水果成篮(未掌握)

1. 滑动窗口的思想
2. 如果使用hashset的话，当[3,3,3,1,2,1,1,2,3,3,4]来到1,2,1,1,2,3的3的时候，去除掉了1但是因为2之后还有1，set简单去除1 是不对的
   
3. 转而使用hashMap记录出现的次数，只有次数为0才从hashMap中去除
   

LC76 最小覆盖子串

1. 使用数组countT来分别char是属于s还是t，countT中对应位置的char如果值是正数属于t，负数属于s
2. 遍历s的时候不断减少对应位置的值，但是需要判断这个位置是否是t中的，是t中的需要匹配的个数就减少了
   

LC54螺旋矩阵

1. 不同于LC59螺旋数组II的正方形，这里的矩阵是长方形，因此需要判断最后是否有剩余
2. 如果长宽中最小值是偶数则一定不会剩余，会剩余的情况需要将剩余的长度（chang或者kuan）都加上，因此for循环的终止条件不是chang-1（kuan-1）
   

区间和（一维前缀和）

• 前缀和数组即presum[i]表示nums数组0-i位置上所有数据的和
  

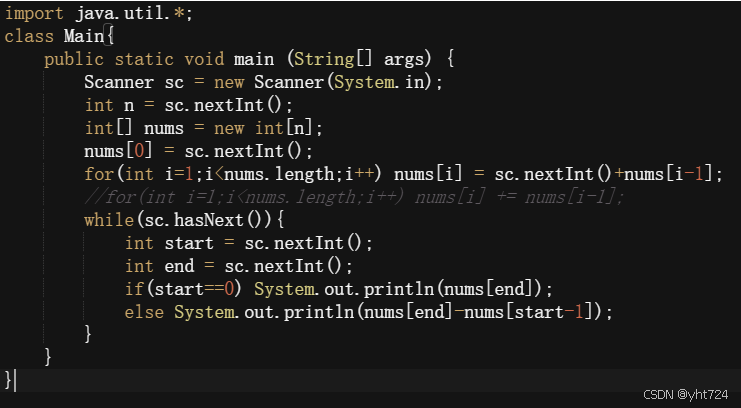
开发商购买土地（二维前缀和）

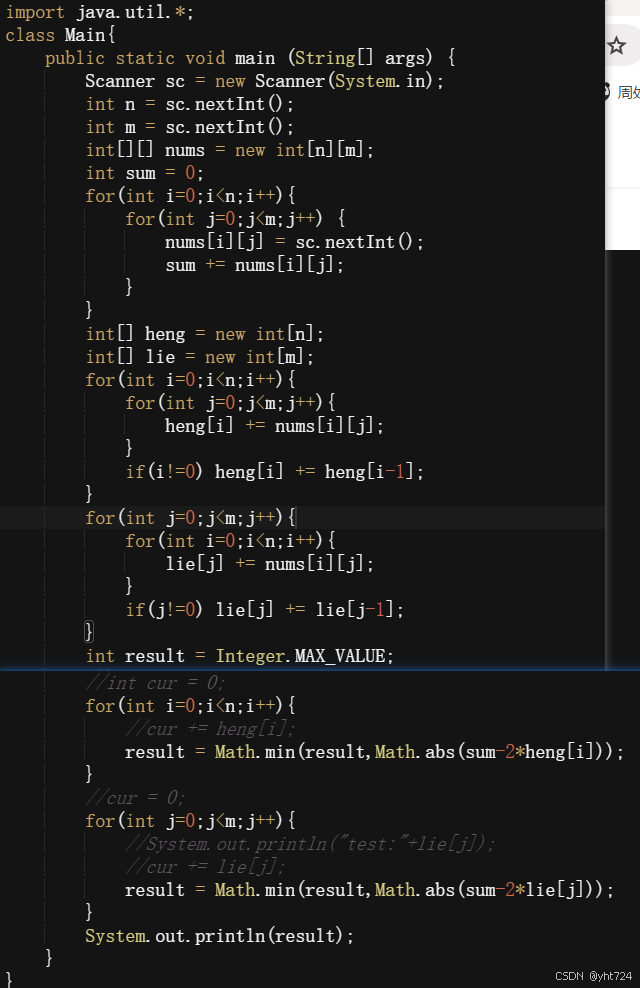
• 二维前缀数组
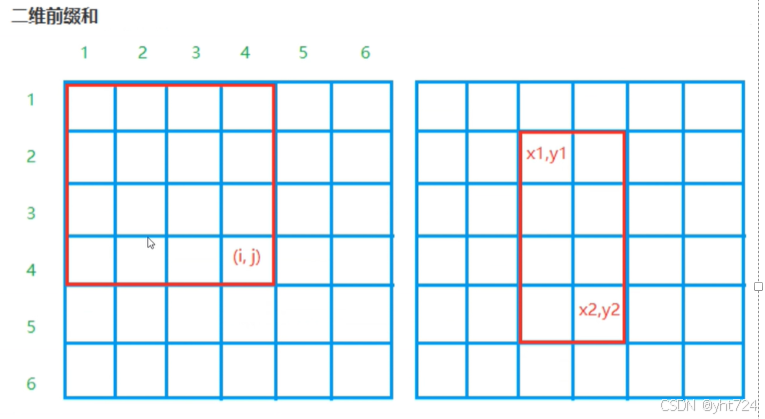
  • presum[i][j]的含义是，nums数组中以[0][0]为左上角，[i][j]为右下角矩阵的前缀和
  • 最普通的递推公式为presum[i][j] = presum[i-1][j]+presum[i][j-1]-presum[i-1][j-1]+nums[i][j]
  • 一维前缀和中，i到j的和为presum[j]-presum[i]===》类推到二维前缀和中，[a][b]为左上角[i][j]为右下角组成的矩阵前缀和为presum[i][j]-presum[i][b-1]-presum[a-1][j]+presum[a-1][b-1]
  • 更进一步，[i][j]为右下角组成的边长为k的正方形矩阵前缀和为presum[i][j]-presum[i-k][j]-presum[i][j-k]+presum[i-k][j-k]
    
  • 划分区域只能横或者竖，那么就算求presum[n][m]-pre[i][m]和pre[i][m]之间差最小值或者presum[n][m]-pre[n][j]和pre[n][j]之间差最小值
    

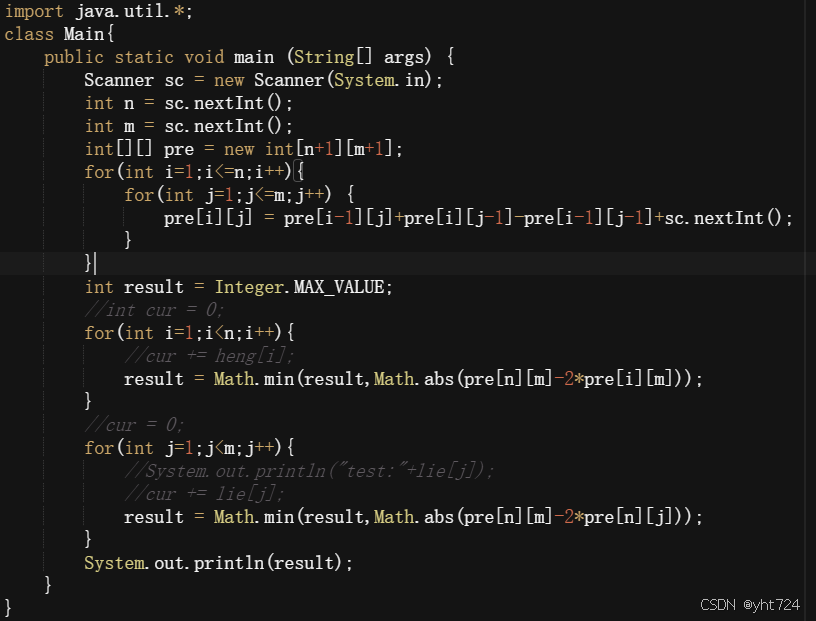
数组常见题型：

• 二分法：
  • 循环不变量原则，两种写法left<=right=》right = mid-1和left<right=》right = mid
• 双指针：通过一个快指针和慢指针在一个for循环下完成两个for循环的工作
• 滑动窗口：根据当前子序列和大小的情况，不断调节子序列的起始位置
• 前缀和