LC647回文子串(未掌握)
- 暴力:两层for循环,遍历区间起始位置和终止位置,然后还需要一层遍历判断这个区间是不是回文。所以时间复杂度:O(n^3)
- dp数组含义
- 常规dp数组:题目求什么,我们就如何定义dp数组。但是此题这样定义很难找到对应的递归关系
- 根据回文性质来定义dp数组:判断一个子字符串(字符串的下表范围[i,j])是否回文,依赖于,子字符串(下表范围[i + 1, j - 1])) 是否是回文
- dp[i][j]:表示区间范围[i,j] (注意是左闭右闭)的子串是否是回文子串
- 递推公式:
- s[i]!=s[j]:dp[i][j]=false
- s[i]==s[j]:
- i==j:dp[i][j]=true
- (j-i)==1:dp[i][j]=true
- (j-i)>1:dp[i][j]由dp[i+1][j-1]决定
- 递归顺序:dp[i][j]由dp[i+1][j-1]决定,且j>=i,因此遍历顺序为正方形上三角,从下往上,从左往右
- 代码

LC516最长回文子序列(未掌握)
- dp[i][j]:字符串s在[i, j]范围内最长的回文子序列的长度为dp[i][j]。
- 递推公式
- s[i]==s[j]:dp[i][j]=dp[i+1][j-1]+2
- s[i]!=s[j]:
- 说明s[i]和s[j]的同时加入 并不能增加[i,j]区间回文子序列的长度,那么分别加入s[i]、s[j]看看哪一个可以组成最长的回文子序列。
- dp[i][j]=Math.max(dp[i+1][j],dp[i][j-1])
- 代码
- 需要注意i=j时,dp[i][j]=1
- 因此j从i+1开始

LC3122使矩阵满足条件的最少操作次数(未掌握)
-
题目对矩阵的要求为:列数字一样,相邻列的数字不一样
-
dp[i][j]数组的含义定义为数组grid第i列全为数字j时满足题目要求的最小操作次数
- 定义count[i][j]数组统计第i列数字j的频率
- 当i=0的时候,dp[i][j] = m-count[i][j]
- 当i不等于0的时候,dp[i][j] = Math.min{dp[i-1][k],k不等于j} + m-count[i][j]
-
代码

-
对dp数组进一步优化,采用滚动数组的方式
- 因为在i列的递归方程中需要使用到i-1列,如果像以往滚动数组直接对dp数组的值进行修改,将会导致i列取0-9内的第一个值是正确计算的,所以需要保留dp的值,另外new一个数组来保留计算结果,计算完成后再赋值给dp
- 代码

LC2400. 恰好移动 k 步到达某一位置的方法数目
- 暴力:从startpos出发,暴力递归每一种走向(左或右)
- 动态规划:dp数组的含义定义为从startpos出发走到i位置用j步的方法数,完全背包排列类型题目
- 因为1 <= startPos, endPos, k <= 1000,且可能出现一直左走的情况,因此i的范围从从-999到2000,递归中还需要考虑边界再往左或者右,因此i范围为-1000到2001。所以dp初始化为【3002】【k+1】
- -1000对应0,所以循环过程中需要+1000
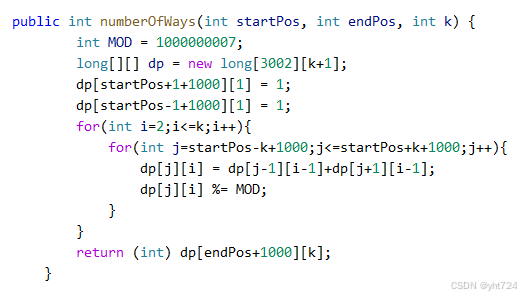
- 代码:






















 1558
1558

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








