一、要解决什么问题
在求取有约束条件的优化问题时,拉格朗日乘子法和KKT条件是非常重要的两个求取方法。
1)对于等式约束的优化问题,可以应用拉格朗日乘子法去求取最优值;
2)如果含有不等式约束,可以用于KKT条件去求取。
当然,这两个方法求得的结果只是必要条件,只有当是凸函数的情况下,才能保证是充分必要条件。
二、解决问题的思路
为什么拉格朗日乘子法和KKT条件能够起作用,为什么要这样去求取最优值呢?
KKT条件是一个必要条件,最小值必须要满足KKT条件,但是不一定是充分条件。
KKT条件反应:目标函数f(x)的梯度df被起作用的不等式约束函数g(x)的负梯度线性表现且系数u全部非负(红色箭头被绿色箭头夹在中间)。其它不等式不起作用的约束函数g(x)的KKT乘子u为0。
2.1 优化问题
1、无约束的优化问题
minf(x)
f(x)在局部极小值点x*处的梯度必然为0,这个梯度为0的条件是局部极小值点的必要条件。
这样,优化问题的求解变成了对该必要条件解方程组。
2. 带等式约束的优化问题
minf(x)
s.t. h(x) = 0.
与无约束的问题不同。我们所要求的极小值点被限制在曲线h(x)=0上,我们将{x|h(x)=0}称为可行域,解只能在这个可行域里取。
如下图所示,曲线h(x)=0经过无约束极小值点(黑点)附近。那么满足约束的极小值点应该与黑点尽可能近。我们将f(x)的等高线不断放大,直到与曲线h(x) = 0相切,切点即为所求。相切是关键,是极小点的必要条件。
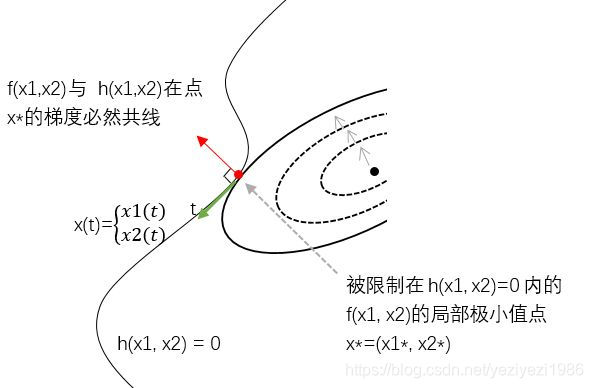
原始问题转换成了如下拉格朗日函数:
![]()
令其偏导为0,正好就得到拉格朗日条件
如此,带等式约束的优化问题转化为了无约束的优化问题,只需要对拉格朗日条件解方程即可。
这里lamda是拉格朗日乘子,有多少个等式约束就有多少个拉格朗日乘子。
3.带不等式约束的优化问题
minf(x),
s.t.
h(x)<=0,
当只有一个不等式其作用时,如我们把问题2的等式约束h(x)=0改为h(x)<=0,如下图所示,可行域变成了阴影部分,最小值还是切点,情况和问题2完全一样,只需要把不等号当做等号去求解即可。
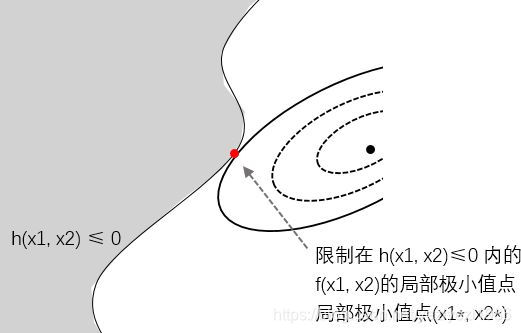
当两个不等式起作用时,那么问题就来了
minf(x),
s.t.
g1(x)<=0,
g2(x)<=0.
如下图,当f(x)的等高线慢慢扩大时,等高线与可行域(阴影部分)第一次相遇的点是个顶点,2个不等式同时起作用了。满足约束的最小值点从原来的黑点位置(切点)移动到了红点位置,现在跟哪条约束函数曲线都不相切。这时候就需要用到KKT条件了。
这里的KKT“条件”是指:某一个点如果是最小值点的话,就必须满足这个条件(在含不等式约束的优化问题里)。这是必要条件。
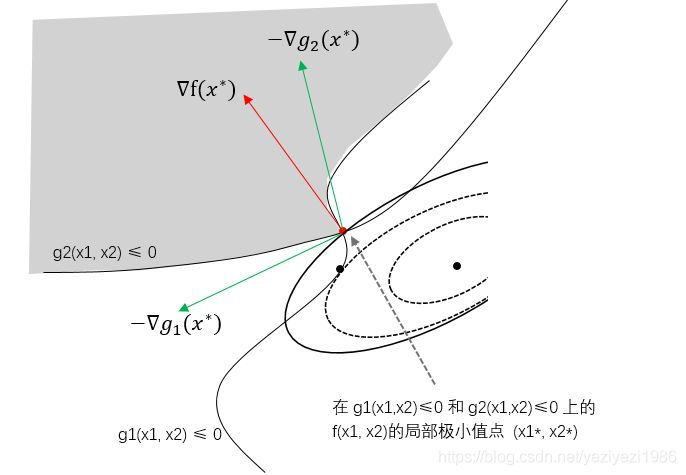
这个问题的解x*应满足的KKT条件为:

其中,μ叫KKT乘子,有多少个不等式约束就有多少个KKT乘子。加上问题3中的约束部分,就是完整版的KKT条件。对于有等式的情况,你把其中一个不等式约束换成等式,可行域变成了半条曲线,最小值点还是那个红点,和下面这种情况是一样的。
下面看看KKT条件是怎么来的:
在问题2中我们知道了约束曲线的梯度方向与曲线垂直,我在上图画出了两条约束曲线的负梯度方向(绿色箭头)和等高线的梯度想法(红色箭头)。如果这个顶点是满足约束的最小值点,那么该点处(红点),红色箭头一定在两个绿色箭头之间(-dg方向一定指向g(x)减小的方向,即g(x)<0的那一边)。即df(x*)能被-dg1和-dg2线性表达(df = -u1*dg1 - u2*dg2),且系数必须非负(u1>=0, u2>=0)。也就是KKT条件中的1和2.
有时候,有的不等式约束实际上不起作用,如下面这个优化问题

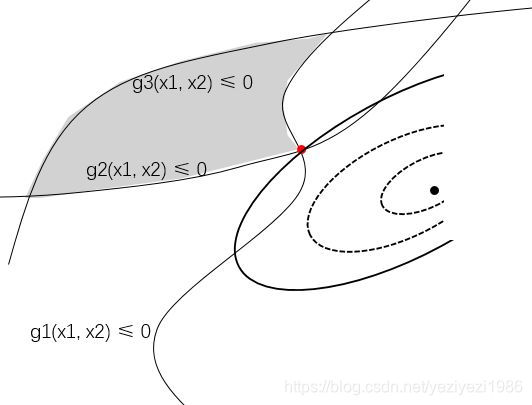


了几个不起作用的不等式约束,条件2都能完美实现:目标函数f(x)的梯度df被起作用的不等式约束函数g(x)的负梯度线性表现且系数u全部非负(红色箭头被绿色箭头夹在中间)。这样,优化问题的求解就变成了对所有KKT条件解方程组。
如果再等一一个拉格朗日函数
![]()
令它对x的偏导为0,就是KKT条件中的条件2了。
优化问题的求解变成了对所有KKT条件解方程组。
整理一遍KKT条件:

最后说明一下,以上所有都是局部极小值点的必要条件。据此求得的解不一定是局部极小值点。原因是上图中我所画的等高线也许根本就不闭合,也就说我们一直想要靠近的等高线中间的黑点压根就是个鞍点或者近似鞍点!
四、为什么SVM要用拉格朗日对偶算法来解最大化间隔问题?
























 7425
7425

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








