POJ3070 Fibonacci(矩阵快速幂)

最新推荐文章于 2021-09-24 14:28:56 发布

原创最新推荐文章于 2021-09-24 14:28:56 发布 · 456 阅读

0 ·

CC 4.0 BY-SA版权

------- 数据结构 ------ 同时被 3 个专栏收录

122 篇文章

订阅专栏

---- POJ -----

96 篇文章

订阅专栏

-- 矩阵快速幂 -----

6 篇文章

订阅专栏

本文介绍了一种高效的方法来计算Fibonacci数列中任意位置的数的最后四位数字，并通过矩阵快速幂算法实现了这一目标。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

B - Fibonacci

Time Limit:1000MS Memory Limit:65536KB 64bit IO Format:%I64d & %I64u

Submit Status

Description

In the Fibonacci integer sequence, F₀ = 0, F₁ = 1, and F_n = F_n_{− 1} + F_n_{− 2} for n ≥ 2. For example, the first ten terms of the Fibonacci sequence are:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …

An alternative formula for the Fibonacci sequence is

Given an integer n, your goal is to compute the last 4 digits of F_n.

Input

The input test file will contain multiple test cases. Each test case consists of a single line containing n (where 0 ≤ n ≤ 1,000,000,000). The end-of-file is denoted by a single line containing the number −1.

Output

For each test case, print the last four digits of F_n. If the last four digits of F_n are all zeros, print ‘0’; otherwise, omit any leading zeros (i.e., print F_n mod 10000).

Sample Input

Sample Output

Hint

As a reminder, matrix multiplication is associative, and the product of two 2 × 2 matrices is given by

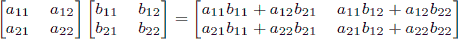Also, note that raising any 2 × 2 matrix to the 0th power gives the identity matrix:

Source Code

#include <stdio.h>
#include <math.h>
#include <string.h>
#include <stdlib.h>
#include <iostream>
#include <algorithm>
#include <set>
#include <map>
#include <queue>
using namespace std;
const int inf=0x3f3f3f3f;
const int mod=10000;
int n = 2;
struct node
{
    int mp[20][20];
} init,res;
struct node Mult(struct node x, struct node y)// 矩阵相乘
{
    struct node tmp;
    int i,j,k;
    for(i=0; i<n; i++)
    {
        for(j=0; j<n; j++)
        {
            tmp.mp[i][j]=0;
            for(k=0; k<n; k++)
            {
                tmp.mp[i][j]=(tmp.mp[i][j]+x.mp[i][k]*y.mp[k][j])%mod;
            }
        }
    }
    return tmp;
};
struct node expo(struct node x, int k)//矩阵快速幂
{
    struct node tmp;
    int i,j;
    for(i=0; i<n; i++)
    {
        for(j=0; j<n; j++)
        {
            if(i==j)
            {
                tmp.mp[i][j]=1;
            }
            else
            {
                tmp.mp[i][j]=0;
            }
        }
    }
    while(k)
    {
        if(k%2 == 1)
        {
            tmp=Mult(tmp,x);
        }
        x=Mult(x,x);
        k>>=1;
    }
    return tmp;
};
int main()
{
    int T,i,j,k;
    int ans;
    while(~scanf("%d",&k))
    {
        if(k == -1)
        {
            break;
        }
        if(k == 0)
        {
            printf("0\n");
            continue;
        }
        init.mp[0][0] = 1;
        init.mp[0][1] = 1;
        init.mp[1][0] = 1;
        init.mp[1][1] = 0;
        res=expo(init,k);
        ans = res.mp[0][1];
        printf("%d\n",ans);
    }

return 0;
}