| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 27275 | Accepted: 9317 |
Description
A tree is a well-known data structure that is either empty (null, void, nothing) or is a set of one or more nodes connected by directed edges between nodes satisfying the following properties.
There is exactly one node, called the root, to which no directed edges point.
Every node except the root has exactly one edge pointing to it.
There is a unique sequence of directed edges from the root to each node.
For example, consider the illustrations below, in which nodes are represented by circles and edges are represented by lines with arrowheads. The first two of these are trees, but the last is not.
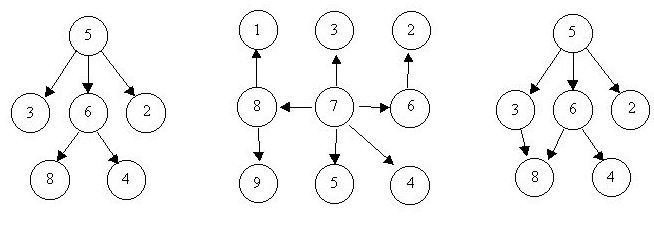
In this problem you will be given several descriptions of collections of nodes connected by directed edges. For each of these you are to determine if the collection satisfies the definition of a tree or not.
There is exactly one node, called the root, to which no directed edges point.
Every node except the root has exactly one edge pointing to it.
There is a unique sequence of directed edges from the root to each node.
For example, consider the illustrations below, in which nodes are represented by circles and edges are represented by lines with arrowheads. The first two of these are trees, but the last is not.

In this problem you will be given several descriptions of collections of nodes connected by directed edges. For each of these you are to determine if the collection satisfies the definition of a tree or not.
Input
The input will consist of a sequence of descriptions (test cases) followed by a pair of negative integers. Each test case will consist of a sequence of edge descriptions followed by a pair of zeroes Each edge description will consist of a pair of integers; the first integer identifies the node from which the edge begins, and the second integer identifies the node to which the edge is directed. Node numbers will always be greater than zero.
Output
For each test case display the line "Case k is a tree." or the line "Case k is not a tree.", where k corresponds to the test case number (they are sequentially numbered starting with 1).
Sample Input
6 8 5 3 5 2 6 4 5 6 0 0 8 1 7 3 6 2 8 9 7 5 7 4 7 8 7 6 0 0 3 8 6 8 6 4 5 3 5 6 5 2 0 0 -1 -1
Sample Output
Case 1 is a tree. Case 2 is a tree. Case 3 is not a tree.
Source
这道题做了好长时间,判断是不是树,并且是有向图,用了加权规则,第一次接触,这里附加一点加权规则的解释
Union操作的加权规则
为避免产生退化的树,改进方法是先判断两集合中元素的个数,如果以 i 为根的树中的结点个数少于以 j 为根的树中的结点个数,即parent[i] > parent[j],则让 j 成为 i 的双亲,否则,让i成为j的双亲。此即Union的加权规则。
#include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std;
int pre[110000],vis[110000],flag,ran[110000];
int find(int x)
{
if(x==pre[x])
return x;
return pre[x]=find(pre[x]);
}
void join(int x,int y)
{
int fx=find(x);
int fy=find(y);
if(fx!=fy)
{
if(ran[fx]<ran[fy])//fx的节点多
{
pre[fx]=fy;//fy指向fx
}
else
{
pre[fy]=fx;
if(ran[fx]==ran[fy])
ran[fx]++;
}
}//用加权规则得到的树
else flag=0;
}
int i,j,k,l,m,n,a,b,ans;
int main()
{
l=1;
while(1)
{
if(m<0||n<0)
break;
k=0;
ans=0;
for(i=1;i<110000;i++)
{
pre[i]=i;
vis[i]=0;
ran[i]=0;
}
flag=1;
while(~scanf("%d%d",&m,&n))
{
k++;
if(m==0&&n==0)
break;
if(m<0||n<0)//要再判断一下
return 0;
vis[m]=1;//并不是每一个点都用过,这里要记录用过的点
vis[n]=1;
join(m,n);
}
int ans=0;
for(i=1;i<110000;i++)
{
if(pre[i]==i&&vis[i])
ans++;
if(ans>1)
{
flag=0;
break;
}
}
if(k==1)//0 0也是树
printf("Case %d is a tree.\n",l++);
else if(flag)
printf("Case %d is a tree.\n",l++);//输出格式一定要看清
else printf("Case %d is not a tree.\n",l++);
}
}师傅说:这道题也可以不用并查集,先记录用过的点,再储存一下每个点的入度,大于1的就不是一颗树,如果用到了n个点,并且有n-1条边,该图就是一颗树,这里也贴一下代码
#include<algorithm>
#include<stdio.h>
#include<string.h>
using namespace std;
int f[100005];
int main()
{
int a,b,flag,i,j;
int t=1;
while(1)
{
j=0;
i=0;
flag=0;
memset(f,0,sizeof(f));
while(scanf("%d%d",&a,&b)&&a&&b)
{
if(a<0||b<0)
return 0;
if(f[b]-1==1)
flag=1;
if(f[a]==0)
j++;
if(f[b]==0)
j++;
f[a]=1;f[b]=2;i++;
}
if(flag==0&&j==i+1)
printf("Case %d is a tree.\n",t++);
else printf("Case %d is not a tree.\n",t++);
}
}








 本文介绍了一种算法来判断给定的有向图是否符合树的定义。通过使用加权并查集的方法,文章详细阐述了如何通过输入的边来确定图是否构成一棵树,并提供了两种不同的实现方式。
本文介绍了一种算法来判断给定的有向图是否符合树的定义。通过使用加权并查集的方法,文章详细阐述了如何通过输入的边来确定图是否构成一棵树,并提供了两种不同的实现方式。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








