文献阅读记录（三十三）2023-08-25

憨化龙猫

已于 2023-08-26 20:26:39 修改

阅读量128

点赞数

CC 4.0 BY-SA版权

文章标签：学习

于 2023-08-25 12:02:36 首次发布

本文链接：https://blog.youkuaiyun.com/yangmoua/article/details/132485824

本文介绍了一种名为HAKE的层次感知知识图嵌入模型，它通过模量和相位部分区分不同层级和同一层级的实体，用于提升知识图谱链接预测的准确性。模型利用实体深度和关系的符号信息，结合极坐标表示，有效捕捉语义层次结构。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

文献名称：Learning Hierarchy-Aware knowledge Graph Embeddings for Link prediction（用于链路预测的学习层次感知知识图嵌入）

为了对知识图谱的语义层次结构进行建模，知识图嵌入模型必须能够区分以下两类实体。1.层次结构中不同级别的实体。例如，“哺乳动物”和“狗”，“奔跑”和“移动”。2.层次结构中处于同一级别的实体。例如，“玫瑰”和“牡丹”，“卡车”和“汽车”。

为了对上述两个类别进行建模，提出了一个层次感知的知识图嵌入模型——HAKE（Hierarchy-Aware knowledge Graph Embedding）。HAKE由两个部分组成——模量(modulus)部分和相位(phase)部分。

为了区分不同部分中的嵌入，在模量部分中，使用 $\mathbf{e}_m$ （e可以是h或t）和 $\mathbf{r}_m$ 来表示实体嵌入和关系嵌入，而在相位部分中使用 $\mathbf{e}_p$ （e可以为h或t）和 $\mathbf{r}_p$ 来表示相位(phase)部分中的主体嵌入和关系植入。

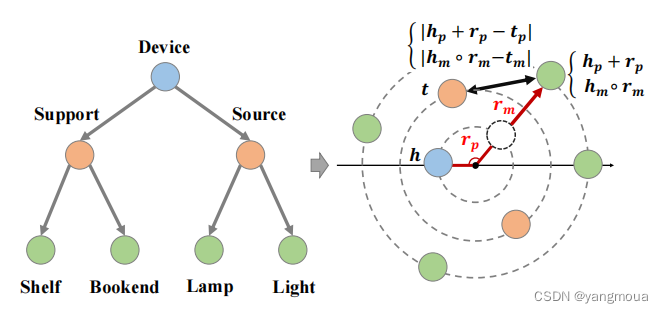
模量部分：对层次结构中不同级别的实体进行建模，因为具有层次属性的实体可以被视为树，我们可以使用节点（实体）的深度来对层次的不同级别进行建模，因为模量可以关联树中的深度。将 $\mathbf{h}_m$ 和 $\mathbf{t}_m$ 的每个条目，即 $[\mathbf{h}_m]_i$ 和 $[\mathbf{t}_m]_i$ ，视为一个模，并将 $\mathbf{r}_m$ 的每个条目（即 $[\mathbf{r}_m]_i$ ）视为两个模之间的尺度变换。将模量部分表述为：

$\mathbf{h}_m\circ \mathbf{r}_m=\mathbf{t}_m;\mathbf{h}_m,\mathbf{t}_m\in R^{k},\mathbf{r}_m\in R^{k}$

对应的距离函数为：

$d_{r,m}(\mathbf{h}_m,\mathbf{t}_m)=\left \| \mathbf{h}_m\circ \mathbf{r}_m -\mathbf{t}_m\right \|_2$

允许实体嵌入的条目（entry）为负，但限定关系嵌入的条目为正。这是因为实体嵌入的符号可以帮助我们预测两个实体之间是否存在关系。例如，如果在h和t1之间存在关系r，h和t2之间不存在关系，那么 $(h,r,t_1)$ 是一个正样本，而 $(h,r,t_2)$ 是一个负样本。目标是最小化 $d_r(\mathbf{h}_m,\mathbf{t}_{1,m})$ 和最大化 $d_r(\mathbf{h}_m,\mathbf{t}_{2,m})$ ，以便明确区分正样本和负样本。对于正样本， $[\mathbf{h}]_i$ 和 $[\mathbf{t}_1]_i$ 倾向于共享相同的符号，因为 $\mathbf{[r_{m}]}_{i}>0$ 。对于负样本，如果我们随机初始化它们的符号，那么它们的符号 $\mathbf{[h_{m}]}_{i}$ 和 $\mathbf{[t_{2,m}]}_{i}$ 将会不相同。以这种方式， $d_r(\mathbf{h}_m,\mathbf{t}_{2,m})$ 更可能大于 $d_r(\mathbf{h}_m,\mathbf{t}_{1,m})$ 。此外，可以期望层次结构中更高层次的实体具有更小的模量，因为这些实体更接近树的根。
如果只使用模量部分来嵌入知识图，则层次结构中处于同一级别的实体将具有相同的模量。此外，假设 r 是一个关系，反映了相同的语义层次，那么 $[\mathbf{r}]_i$ 将趋于1，因为 $h\circ r\circ r=h$ 对于所有h都成立。此处的 r是表示相同的语义层次，两个实体之间是 r 关系，表明这两个实体是在同一个层次上。也就是对于实体 h ，与关系 r 进行运算后，仍然是实体 h 。就是在层次A上的实体与关系 r 进行运算后，仍在层次A上。

相位部分（phase）：因为在同一个圆上的点的模量相同而相位不同，使用相位信息来区分同一层语义层次的实体，进行建模。将 $\mathbf{h}_{p}$ 和 $\mathbf{t}_{p}$ 的每一项即 $[\mathbf{h}_{p}]_i$ 和 $[\mathbf{t}_{p}]_i$ 视为相位，并且将 $\mathbf{r}_{p}$ 的每一项，即 $[\mathbf{r}_{p}]_i$ 视为相位转换。我们可以将相位部分表述如下：

$\left(\mathbf{h}_{p}+\mathbf{r}_{p}\right) \bmod 2 \pi=\mathbf{t}_{p}, \text { where } \mathbf{h}_{p}, \mathbf{r}_{p}, \mathbf{t}_{p} \in[0,2 \pi)^{k}$

相应的距离函数为：

$d_{r, p}\left(\mathbf{h}_{p}, \mathbf{t}_{p}\right)=\left\|\sin \left(\left(\mathbf{h}_{p}+\mathbf{r}_{p}-\mathbf{t}_{p}\right) / 2\right)\right\|_{1}$

其中sin(.)是将正弦函数应用于输入的每个元素的运算。由于相位具有周期性特征，因此使用正弦函数来测量相位间的距离，而不是使用 $\left\|\mathbf{h}_{p}+\mathbf{r}_{p}-\mathbf{t}_{p} \right\|_{1}$ .该距离函数与pRostatE具有相同的公式。

HAKE将模量部分和相位部分组合在一起，将实体映射到极坐标系中，其中径向坐标和角坐标分别对应于模量部分和相位部分。也就是说，HAKE将一个实体h映射到[hm;hp]，其中hm和hp分别由模量部分和相位部分产生， [·;·]表示两个向量的串联。显然， $\left (\left [ h_{m} \right ]_{i} ,\left [ h_{p} \right ]_{i} \right )$ 是极坐标系中一个2D的点坐标。具体把HAKE公式定义如下：

$\{^{h_{m}\circ r_{m}=t_m;h_m,t_m\in R^{k},r_{m}\in R^{k}_{+},}_{(h_{p}+r_p)mod2\pi =t_p;h_p,t_p,r_p\in [0,2\pi )^{k}}$

HAKE的距离函数是：

$d_r(h,t)=d_{r,m}(h_m,t_m)+\lambda d_{r,p}(h_p,t_p)$

$\lambda$ 是模型学习的参数。相应的得分函数为：

$f_{r}(h,t)=d_r(h,t)=-d_{r,m}(h,t)-\lambda d_{r,p}(h,t)$

但两个实体有相同的模，模部分的距离为0.相位部分的可能非常大。通过结合模部分和阶段部分，HAKE可以对两类中的实体进行建模。因此，HAKE可以对知识图的语义层次进行建模。在评估模型时，发现在 $d_{r,m}\left ( h,t \right )$ 中加入混合偏差(mixture bias)有助于提高HAKE的性能。修正的 $d_{r,m}\left ( h,t \right )$ 由下式得出：

$d^{'}_{r,m}(\mathbf{h},\mathbf{t})=\left \| \mathbf{h}_m\circ \mathbf{r}_m +(\mathbf{h}_m+\mathbf{t}_m )\circ \mathbf{r}^{'}_m-\mathbf{t}_m\right \|_2$