论文阅读|ResNetv2:Identity Mappings in Deep Residual Networks

本文链接：https://blog.youkuaiyun.com/yanghao201607030101/article/details/110832192

首先回顾ResNetv1，这里把第一版本的ResNet叫做原始版本，原始版本中的网络结构由大量残差单元（“Residual Units”）组成，原文中的残差单元有两种(见图1)，一种是building block，一种是“bottleneck” building block，本文中以building block为例。
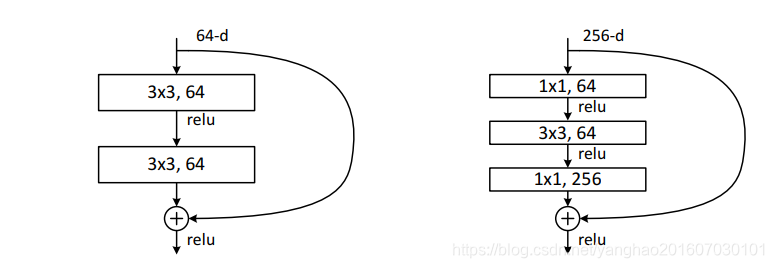
在这里插入图片描述
图1.原版本ResNet中提到的两种残差单元。左边是building block，右边是“bottleneck” building block。二者计算量接近，但是右边能取得更好性能。

这些残差单元，可由以下公式表示：
$y_l = h(x_l) + F(x_l, W_l) , (1)$ $x_{l+1} = f(y_l),(2)$
xl和xl+1分别为第l个单元的输入和输出, $F$ 代表残差函数， $h(x_l)=x_l$ 代表恒等映射（identity mapping ）, $f$ 代表ReLU。

该篇论文主要聚焦于构建一条贯通全网络的直通车道，使得前向传播和反向传播都能在这条通道上很好的传播信息，减少因网络层增加而带来的信息损失，也即梯度信息损失等，使得网络能够够造更深层的网络。

作者推导得出，如果 $h(x_l)$ 和 $f(y_l)$ 都是恒等映射，那么前向传播和反向传播的信号就能直接从一个单元传到任意一个其他单元。并且实验证明，但网络接近以上两个条件时网络更容易训练。
下面是推理：
当 $h(x_l)$ 和 $f(y_l)$ 都是恒等映射时，即 $h(x_l)=x_l$ ， $x_{l+1} =f(y_l)≡ y_l$ 。然后上面等式(1)就变成了下面的等式(3)。
$x_{l+1} = x_l + F(x_l, W_l),(3)$

再把 $x_{l+2} = x_{l+1}+ F(x_{l+1} ,W_{l+1})= x_l + F(x_l, W_l)+F(x_{l+1} ,W_{l+1})$ 等循环带入，得到：
$xL=xl+∑i=lL−1F(xi,Wi),（4）x_L=x_l+\sum_{i=l}^{L-1}F(x_i,W_i),（4）$
这样有两个好处：

任何一个深层的残差单元 $L$ 就能被表示维一个任意的浅层残差单元 $l$ 加上一个残差函数 $∑i=lL−1F\begin{matrix}\sum_{i=l}^{L-1}F \end{matrix}$
任何一层的残差单元L的特征变成之前所有层的残差函数之和，再加上 $x_0$ ，即 $xL=x0+∑i=lL−1F(xi,Wi)x_L=x_0+\begin{matrix}\sum_{i=l}^{L-1}F (x_i,W_i)\end{matrix}$ 。这一点于普通网络形成对比，普通网络这里是等于前面所有网络的矩阵乘积相乘（忽略掉ReLU和BN）。
于是，我们可以说在前向传播方向，我们的直通车道是可行的。下面再说说另一个通道——反向传播方向。

由等式4能够得到一个很好的反向传播性质，这里将损失函数指代 $ε\varepsilon$ ，
$\frac {\partial \varepsilon}{\partial x_l}= \frac {\partial \varepsilon}{\partial x_L}\frac {\partial x_L}{\partial x_l}=\frac {\partial \varepsilon}{\partial x_L} \left(1+ \frac{\partial}{\partial x_l} \sum_{i=l}^{L-1}F(x_i,W_i)\right).(5)$
上面等式5将梯度 $∂ε∂xl\frac {\partial \varepsilon}{\partial x_l}$ 分解成两部分，一个部分是 $∂ε∂xL\frac {\partial \varepsilon}{\partial x_L}$ ，该部分确保了梯度信号能够直接从 $L$ 层传到 $l$ 层而不需要考虑残差函数；另一部分是 $∂ε∂xL\frac {\partial \varepsilon}{\partial x_L}$ $∂∂xl∑i=lL−1F(xi,Wi)\frac{\partial}{\partial x_l} \sum_{i=l}^{L-1}F(x_i,W_i)$ ,这部分通过残差结构传播。即等式5表面反向传播通道，信号能够从深层 $L$ 传递到任意浅层 $l$ 。