论文阅读学习 - ResNet - Identity Mappings in Deep Residual Networks

最新推荐文章于 2025-03-26 12:38:52 发布

原创

最新推荐文章于 2025-03-26 12:38:52 发布 · 933 阅读

3 ·

CC 4.0 BY-SA版权

文章标签：

#恒等映射 #ResNet

本文详细分析了ResNet中的恒等映射在深度残差网络中的作用，指出其能有效避免梯度消失问题，促进信息在前向和后向传播中的直接传递。通过对比不同类型的恒等映射，证明了使用恒等跳跃链接和预激活层（ReLU和BN）的残差单元有利于网络训练和泛化。实验表明，恒等映射的使用对于网络优化至关重要，防止了梯度消失和爆炸，确保了模型的有效学习。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

论文阅读学习 - ResNet - Identity Mappings in Deep Residual Networks

[Paper]

[Code-Torch - Deep Residual Networks with 1K Layers]

摘要:

对深度残差网络理论分析.

残差构建模块中，采用恒等映射(identity mapping)作为 skip connetions 和 after-addition activation时， forward 和 backward 可以从一个 block，直接传递到任何其他 blocks.

阐述恒等映射的重要性.

1. 残差单元和跳跃链接 Skip Connections

深度惨差网络ResNets 是由许多堆积的残差单元 Residual Units 组成.

如 Fig (a). 每个残差单元可以表示为：

$\mathbf{y}_l = h(\mathbf{x_l}) + \mathcal{F}(\mathbf{x}_l, \mathcal{W}_l)$ (1)

$\mathbf{x}_{l+1} = f(\mathbf{y}_l)$ (2)

其中， $\mathbf{x}_l$ 和 $\mathbf{x}_{l+1}$ 为第 $l$ 个残差单元的输入和输出， $\mathcal{F}$ 为残差函数(如，堆积的两个 $3 × 3$ 的卷积层).

$h(\mathbf{x}_l) = \mathbf{x}_l$ 为恒等映射.

$f$ 为 ReLU 函数，element-wise相加后的操作.

$\mathcal{W}_l = \{W_{l,k} | 1 \leq k \leq K \}$ 为第 $l$ 个残差单元的权重集. $K$ 是残差单元的层数( $K=2 或 K=3$ ).

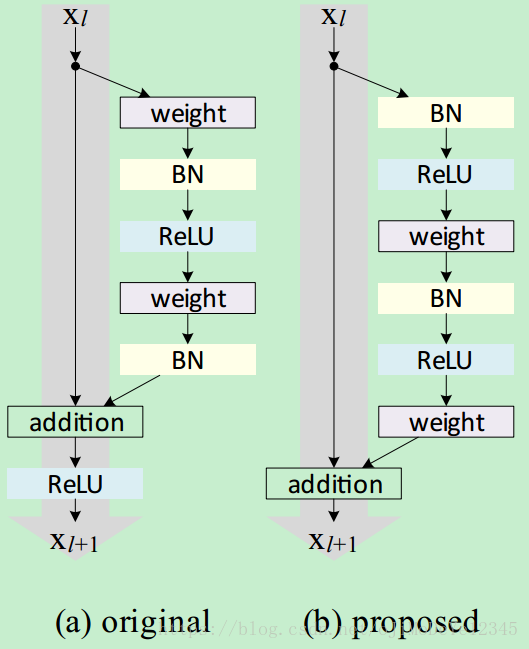
这里写图片描述

ResNets 的关键是，拟合关于 $h(\mathbf{x}_l)$ 的残差函数 $\mathcal{F}$ ( $\mathcal{F} = \mathbf{y} - h(\mathbf{x})$ )时，最佳选择是 $h(\mathbf{x}) = \mathbf{x}$ . 即：通过单位跳跃链接(identity skip connection，shortcut)来实现.

本文所分析的是，创建信息传递的直接路径的深度残差网络，不仅仅是一个残差单元，还包括整个网络.

得出的结论是，如果 $h(\mathbf{x})$ 和 $f(\mathbf{y}_l)$ 都是恒等映射(identity mappings)，信号在前向和后向传递时都可以从一个神经元和其它任何神经元直接传递.