研究三：组合导航（3/3）——GNSS部分

有人说：GPS的定位精度能够达到毫米级定位精度？

妈耶，这让我一个学习定位的就不得不去学习学习了

后来看到这篇贴吧就突然悟了：北斗导航真的能达到毫米级定位精度吗？ - 知乎，不是它一个能够实现毫米级的精度，而是配合一些其他的设备才能够达到毫米级别的精度。

一般的卫星导航需求的最简设备：四颗卫星（是四颗）+用户的接受装置实现卫星定位（四个方程）

但是这样定位为什么定位精度只在米级？主要是因为：导航卫星发射的信号从太空到地面的过程不是一帆风顺的，其在通过电离层、对流层等区域，电磁波信号会发生“延缓”，如果就这样简单的计算位置这导致了地面用户的定位位最后有5~10米左右的误差。不对呀？说好的厘米级别的误差呢？

通俗的说：

为了实现更高精度，米级在高精度定位在研究的的时候肯定不能使用的。不管是中国北斗，还是美国GPS、欧洲Galileo、俄罗斯Glonass，单纯只靠他们自身的星座卫星，定位精度都在米级。如果想要更高精度：

（1）要么就要尽全力滤除这些干扰，但是想滤出干扰达到更高的精度是不现实的。最终可能定位精度在几米之内。

（1）如果我们尽力滤波的同时另有一台接收机（比方说双天线了）。由于两台接收机距离并不是很远，信号从卫星到达一台接收机天线所受到的大气延时与另外一台几乎是一样的，将两台接收机的距离测量值相减，就能将大气延时误差、星历误差基本消除，但是还是那句话：滤不光，所以定位精度在米级。（RTD）

（2）最终我们需要外界辅助，也就是基站了——在卫星定位的基础之上设定一个地面的基站，根据一系列规则能够减少干扰。。如果再建立更多的基站，建立网络，就能让他实现毫米级别的定位精度。（RTK）

上面说的这两种技术就是非常有名的伪距差分定位(RTD)和载波相位差分定位(RTK)技术

从深层次的角度上来看

（RTK）：用卫星定位的基站位置与基站实际位置有一定的误差，我们再把基站的这种误差告诉其他的接受设备，这样接受的设备就能根据这个误差进行修正（离基站的太远的接受装置就没法修正）

基于上面说的，我们多建造几个基站（或者用其他的方法）建立一个参考基准网络，只要有定位需求的用户设备在里面，总会有三个离他最近的参考基准站把他包围起来。深一点的说：用户设备先用最原始的定位方式算出自己的粗略位置，然后发给计算平台，让计算平台找到离他最近的三个参考基准站，并根据三个基准站的观测数据运用某种算法（当然保密啦，要赚钱的嘛）算出用户设备的的精确坐标，通过Internet或者无线蜂窝发送给许四多。通过此种方法，可以实现厘米级定位。如果毫米级的定位精确计算量又变大了.

所以说：你不付费，哪来的高质量服务，还毫米级

2 GNSS工作原理

简单示意图:

2.1 卫星发射信号

我们从全球定位系统的组成与信号结构开始研究，也就是说：接收机接收卫星发射的信号的种类

载波和测距码主要用于后续的定位，而导航电文主要作用是：

卫星识别和选择：

卫星位置和速度计算：

卫星时钟校正：

导航参数计算：

通过解析和利用导航电文中的数据，接收器能够确定卫星的位置、时钟偏差和其他导航参数，从而进行精确的定位计算。导航电文提供了关键的信息，帮助接收器实现准确的定位和导航功能。

要注意：我们将GPS发送的载波测距码、导航电文（无线电信号）统称为广播信号，如果在融合卫星观测数据和地面测站数据等多种数据源进行处理和计算，就能够得到精密星历

2.2 接受机接受信号

卫星发射的信号经过中间的各种干扰（需要建立误差模型），最后终于被接收机接受，这个时候就能够定位了，而接受的信号主要是利用卫星发射的载波以及测距码来进行定位。

采用测距码定位这种方法是最简单的，但是误差在5-10m

还介绍了：载波相位测量定位

最后一句话说的很清楚：从载波信号定位的一般精度在2-3mm，精度最高的能够达到0.2-0.3mm

当然，误差方程建立和分析是个非常麻烦的过程

2.3 单点定位技术

这一节具体分析了单点定位这门技术：

使用广播星历（卫星发出的信号）的采用伪距信号的定位叫做传统单点定位，使用精密星历（不仅仅式卫星发出的信号，还融合卫星观测数据和地面测站数据等多种数据源进行处理和计算后的信号），采用载波信号的定位叫做精密单点定位。

值得注意的是：在书的后面还有许多的定义：比方说绝对定位和相对定位

绝对定位又称为单点定位，这是一种采用一台接收机进行定位的模式，它所确定的是接收机天线的绝对坐标。这种定位模式的特点是作业方式简单，可以单机作业。绝对定位一般用于导航和精度要求不高的应用中。

相对定位又称为差分定位，这种定位模式采用两台以上的接收机，同时对一组相同的卫星进行观测，以确定接收机天线间的相互位置关系。

动态定位和静态定位就很好理解，静止更容易定位，动态环境更难定位（精度的影响大）

三松组合

参考

GNSS-INS组合导航:KF-GINS(一）_Amentia outsider的博客-优快云博客

KF-GINS：GitHub - i2Nav-WHU/KF-GINS: An EKF-Based GNSS/INS Integrated Navigation System

3.1 构建离散卡尔曼滤波

1.1 构建状态观测方程

首先是构建离散卡尔曼滤波第一步的公式

我们是通过IMU的误差来建立状态方程（含义自己看pdf）

以及通过GINS给出来的速度和位置作为观测

也就是PDF后面推导的公式：

主要是因为松组合GNSS只提供简单的位置和速度，而且GNSS没有累计误差，用来做观测方程就很不错。误差是怎末产生的，从状态方程的角度来看是误差x直接与IMU的各种小误差加权之后在受到噪声的干扰有关，从观测方程的角度来看：误差x直接和IMU和GNSS做差有关。

要分清上面说的状态和量测的定义

在重复一遍：状态x直接与IMU的误差量有关，状态x经过直接反应在GNSS与IMU做差（观测）有关

这样：使用卡尔曼滤波的第一步就确定成功了

1.2 状态量的获取

在实际分析的时候，我们不能够直接获取这些状态信息，而是通过微分间接获取信息，比方说这些参数经过微分能够得到：

如果准确一点，再仔细书写就是：

就能写出状态的一阶导数形式

G矩阵比较简单，但是F的分块矩阵都比较复杂，关系到每种误差的详细定义建议看GNSS-INS组合导航:KF-GINS(一）_Amentia outsider的博客-优快云博客直接给出分块定义

1.3 离散化处理

我们最终的目的是为了得到：

但是1.2得到的是

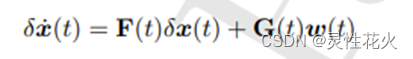
很明显用导数是不对的，所以这里我们需要进行变化，从倒数变换成非导数

这里的变化应该是有一种规则，但是我忘的差不多了：

这样就能够构建一个能用的状态方程了（当然，原PDF还继续验证了是白噪声）

void GIEngine::EKFUpdate(Eigen::MatrixXd &dz, Eigen::MatrixXd &H, 
Eigen::MatrixXd &R) {
 assert(H.cols() == Cov_.rows());
 assert(dz.rows() == H.rows());
 assert(dz.rows() == R.rows());
 assert(dz.cols() == 1);
 // 计算 Kalman 增益
 // Compute Kalman Gain
 auto temp = H * Cov_ * H.transpose() + R;
 Eigen::MatrixXd K = Cov_ * H.transpose() * temp.inverse();
 // 更新系统误差状态和协方差
 // update system error state and covariance
 Eigen::MatrixXd I;
 I.resizeLike(Cov_);
 I.setIdentity();
 I = I - K * H;
 // 如果每次更新后都进行状态反馈，则更新前 dx_一直为 0，下式可以简化
为：dx_ = K * dz;
 // if state feedback is performed after every update, dx_ is always zero before 
the update
 // the following formula can be simplified as : dx_ = K * dz;
 dx_ = dx_ + K * (dz - H * dx_);
 Cov_ = I * Cov_ * I.transpose() + K * R * K.transpose();
}