为了简化二叉查找树的删除操作,我将节点按如下定义:
class Node
{
public int data;
public Node rChild;
public Node lChild;
//增加父节点,目的是为了便于删出节点的操作
public Node parent;
public Node() { }
public Node(int data)
{
this.data = data;
this.rChild = null;
this.lChild = null;
this.parent = null;
}
}
BST类及其相关方法如下,每个操作都有较为详细的注释:
class BST
{
public Node rootnode;
//本来应该构建一个普通树作为示例,但是不方便
//不妨就直接构建二叉查找树作为示例
public void AddNodeToBST(BST tree, int data)
{
Node newnode = new Node(data);
if(tree.rootnode == null)
{
tree.rootnode = newnode;
return;
}
Node current = tree.rootnode;
while (true)
{
if (data < current.data)
{
if(current.lChild == null)
{
current.lChild = newnode;
newnode.parent = current;
return;
}
current = current.lChild;
}
else
{
if (current.rChild == null)
{
current.rChild = newnode;
newnode.parent = current;
return;
}
current = current.rChild;
}
}
}
//前序遍历二叉树
public void PreOrder(Node node)
{
if(node != null)
{
Write(node.data + " ");
PreOrder(node.lChild);
PreOrder(node.rChild);
}
}
//中序遍历二叉树
public void MiddleOrder(Node node)
{
if (node != null)
{
MiddleOrder(node.lChild);
Write(node.data + " ");
MiddleOrder(node.rChild);
}
}
//后续遍历二叉树
public void AfterOrder(Node node)
{
if(node != null)
{
AfterOrder(node.lChild);
AfterOrder(node.rChild);
Write(node.data + " ");
}
}
//层序遍历二叉树
public void LevelOrder(Node node)
{
Queue<Node> queue = new Queue<Node>();
if (node == null) return;
queue.Enqueue(node);
while (queue.Any())
{
Node item = queue.Dequeue();
Write(item.data + " ");
if(item.lChild != null)
{
queue.Enqueue(item.lChild);
}
if (item.rChild != null)
{
queue.Enqueue(item.rChild);
}
}
}
//二叉树增删改查之增
//其实构建二叉树的过程就是增的过程,改某个节点值就是查找到然后修改data值,所以就不再赘述
//二叉树 查找 非递归版本
public bool FindInBST1(Node rootnode , int data)
{
int count = 1;
Node current = rootnode;
while (true)
{
if (current.data == data)
{
WriteLine("找到了,在树的第{0}层", count);
return true;
}
if(data <current.data)
{
if(current.lChild == null)
{
return false;
}
count++;
current = current.lChild;
}
else
{
if(current.rChild == null)
{
return false;
}
count++;
current = current.rChild;
}
}
}
//二叉树 查找 递归版本
public bool FindInBST2(Node rootnode, int data)
{
Node current = rootnode;
if(current == null)
{
return false;
}
else if(current.data == data)
{
return true;
}
else if(data <current.data)
{
return FindInBST2(current.lChild, data);
}
else
{
return FindInBST2(current.rChild, data);
}
}
//二叉树 删除 分为三种情况1.为叶节点 2.只有左或者右子节点 3.左右子节点都有
public void DeleteNode( Node rootnode,int deletedata)
{
//先找到该节点
Node current = rootnode;
if(current.data == deletedata)
{
Delete(current);
}
else if(current == null)
{
WriteLine("要删除的节点不存在");
return;
}
else if(deletedata < current.data)
{
DeleteNode(current.lChild, deletedata);
}
else
{
DeleteNode(current.rChild, deletedata);
}
}
public void Delete(Node deletenode)
{
if(deletenode.lChild == null && deletenode.rChild == null)
{
//说明是叶子节点,直接删除就好
if(deletenode.parent.lChild == deletenode)
{
deletenode.parent.lChild = null;
}
else
{
deletenode.parent.rChild = null;
}
}
else if(deletenode.lChild == null && deletenode.rChild != null)
{
//说明有右节点,没有左节点
Node temp = deletenode;
deletenode = deletenode.rChild;
//直接用该节点的右子节点替换该节点,但是还有两点需要改
//1.新节点的父节点 2.删除节点的父节点的子节点指向
deletenode.parent = temp.parent;
if(temp == temp.parent.lChild)
{
//说明父节点的左子节点指向待删除的节点
temp.parent.lChild = deletenode;
}
else
{
//说明父节点的右子节点指向待删除的节点
temp.parent.rChild = deletenode;
}
}
else if(deletenode.rChild == null && deletenode.lChild != null)
{
//说明有左节点,没有右节点
Node temp = deletenode;
deletenode = deletenode.lChild;
//直接用该节点的右子节点替换该节点,但是还有两点需要改
//1.新节点的父节点 2.删除节点的父节点的子节点指向
deletenode.parent = temp.parent;
if (temp == temp.parent.lChild)
{
//说明父节点的左子节点指向待删除的节点
temp.parent.lChild = deletenode;
}
else
{
//说明父节点的右子节点指向待删除的节点
temp.parent.rChild = deletenode;
}
}
else
{
//其他情况说明左右子树都存在,此时可以寻找它的中序遍历的前一个节点作为替代,这样就是寻找它的左子树最右边的一个节点
//或者可以寻找它的中序遍历的后一个节点作为替代,这样寻找它的右子树最左边的一个节点
//这里采用上述说的第一个方式
Node current = deletenode.lChild;
while (true)
{
if (current.rChild != null)
{
current = current.rChild;
}
else { break; }
}
//删除该节点并不改变该节点的左右子节点和父节点的关系,所以替换值就可以了,然后转化为删除替换节点
deletenode.data = current.data;
Delete(current);
}
}
}
测试如下:
class Program
{
static void Main(string[] args)
{
int[] arr = { 62, 58, 88, 47, 73, 99, 35, 51, 93, 37, 49, 52, 38, 48};
BST tree = new BST();
for (int i = 0; i < arr.Length; i++)
{
tree.AddNodeToBST(tree,arr[i]);
}
WriteLine("前序遍历");
tree.PreOrder(tree.rootnode);
WriteLine();
WriteLine("中序遍历");
tree.MiddleOrder(tree.rootnode);
WriteLine();
WriteLine("后序遍历");
tree.AfterOrder(tree.rootnode);
WriteLine();
WriteLine("按层遍历");
tree.LevelOrder(tree.rootnode);
WriteLine();
//查找
tree.FindInBST1(tree.rootnode, 93);
WriteLine(tree.FindInBST2(tree.rootnode, 37));
//删除
Write("请输入您要删除的数:");
int deletenum = int.Parse(ReadLine());
if(deletenum == tree.rootnode.data)
{
//如果删除根节点,那么就全部删除吧
tree.rootnode = null;
}
else
{
tree.DeleteNode(tree.rootnode, deletenum);
}
tree.MiddleOrder(tree.rootnode);
}
}
结果显示:
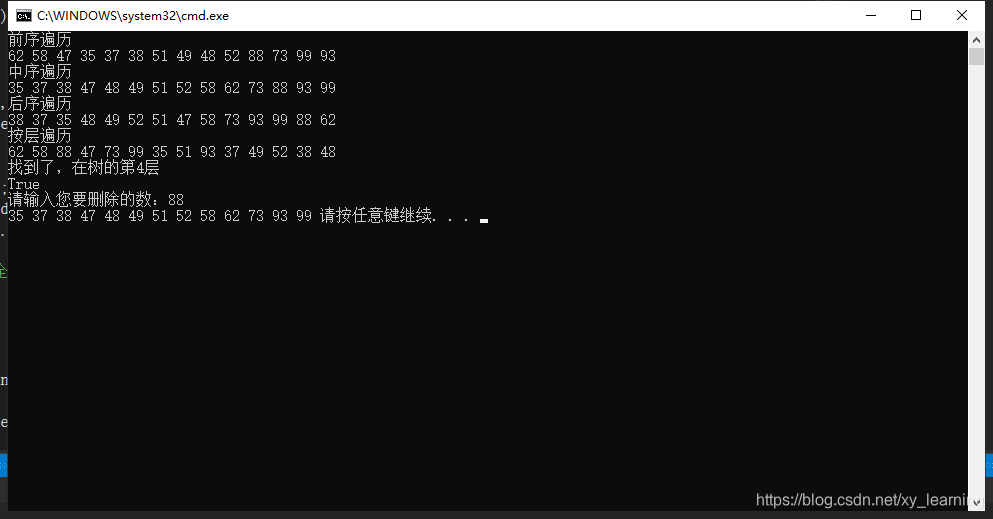
如果有问题请留言。





 本文详细介绍了二叉查找树的插入、查找、删除等基本操作,并提供了完整的代码实现,包括前序、中序、后序及层序遍历方法。通过一个具体的测试案例展示了如何构建、查找和删除节点。
本文详细介绍了二叉查找树的插入、查找、删除等基本操作,并提供了完整的代码实现,包括前序、中序、后序及层序遍历方法。通过一个具体的测试案例展示了如何构建、查找和删除节点。
















 156
156

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








