【LeetCode热题100道笔记】单词搜索

题目描述

给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中，返回 true ；否则，返回 false 。

单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。

示例 1：

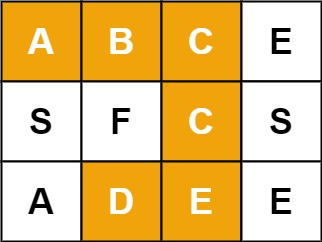
输入：board = [[‘A’,‘B’,‘C’,‘E’],[‘S’,‘F’,‘C’,‘S’],[‘A’,‘D’,‘E’,‘E’]], word = “ABCCED”
输出：true

示例 2：

输入：board = [[‘A’,‘B’,‘C’,‘E’],[‘S’,‘F’,‘C’,‘S’],[‘A’,‘D’,‘E’,‘E’]], word = “SEE”
输出：true

示例 3：

输入：board = [[‘A’,‘B’,‘C’,‘E’],[‘S’,‘F’,‘C’,‘S’],[‘A’,‘D’,‘E’,‘E’]], word = “ABCB”
输出：false

提示：
m == board.length
n = board[i].length
1 <= m, n <= 6
1 <= word.length <= 15
board 和 word 仅由大小写英文字母组成

进阶：你可以使用搜索剪枝的技术来优化解决方案，使其在 board 更大的情况下可以更快解决问题？

思考

在二维矩阵中搜索目标单词，核心是通过深度优先搜索（DFS）+ 回溯实现：

1. 先遍历矩阵找到所有与单词首字母匹配的位置作为起点；
2. 从起点开始，向上下左右四个方向递归探索，每步匹配单词的下一个字符；
3. 用visited矩阵标记已使用的单元格（避免重复使用），回溯时恢复标记，确保其他路径可正常搜索；
4. 若某条路径完全匹配单词，则返回true；所有路径探索完毕仍未匹配则返回false。

算法过程

1. 初始化：

   • 记录矩阵行数m和列数n；
   • 创建visited矩阵（m×n），用于标记单元格是否已在当前路径中使用；
   • 定义结果标识ans（初始为false），用于快速终止搜索。

2. 遍历起点：

   • 遍历矩阵每个单元格(i,j)，若单元格字符与单词首字母word[0]匹配，启动DFS搜索。

3. DFS搜索与回溯：

   • 递归函数dfs(i,j,count)：i,j为当前单元格坐标，count为已匹配的字符数（对应word[count]）。
   • 终止条件：
     • 若count等于单词长度，说明完全匹配，设ans=true并返回；
     • 若越界（i/j超出矩阵范围）、已访问（visited[i][j]=true）或当前字符不匹配word[count]，直接返回。
   • 递归探索：
     • 标记(i,j)为已访问（visited[i][j]=true）；
     • 向上下左右四个方向递归调用dfs，count递增（匹配下一个字符）；
     • 回溯：递归返回后，取消(i,j)的访问标记（visited[i][j]=false），允许该单元格在其他路径中被使用。

4. 结果返回：若任何起点的DFS成功匹配单词，返回true；否则返回false。

复杂度分析

• 时间复杂度：$O(m\times n\times 4^k)$

  • m×n为矩阵单元格总数，每个可能作为起点；
  • 每个起点的DFS最多递归k层（k为单词长度），每层有4个方向可选，故单条路径时间为$4^k$；
  • 最坏情况下需遍历所有起点并探索所有路径，总时间为$O(m\times n\times 4^k)$。

• 空间复杂度：$O(m\times n+k)$

  • visited矩阵占用$O(m\times n)$空间；
  • 递归栈深度最大为k（单词长度），占用$O(k)$空间；
  • 合计为$O(m\times n+k)$，因k最大不超过m×n，可简化为$O(m\times n)$。

代码一

/**
 * @param {character[][]} board
 * @param {string} word
 * @return {boolean}
 */
var exist = function(board, word) {
    const [m, n] = [board.length, board[0].length];
    const visited = Array.from({length: m}, () => Array(n).fill(false));
    
    let ans = false;

    const dfs = function(i, j, count, s) {
        if (count >= word.length) return;
        if (ans || i < 0 || i >= m || j < 0 || j >= n || visited[i][j]) return;

        if (s + board[i][j] === word) {
            ans = true;
            return;
        }

        if (board[i][j] !== word[count]) {
            return;
        }

        visited[i][j] = true;

        dfs(i-1, j, count+1, s + board[i][j]);
        dfs(i+1, j, count+1, s + board[i][j]);
        dfs(i, j-1, count+1, s + board[i][j]);
        dfs(i, j+1, count+1, s + board[i][j]);

        visited[i][j] = false;
    };

    for (let i = 0; i < m;  i++) {
        for (let j = 0; j < n; j++) {
            if (ans) return true;
            if (board[i][j] === word[0]) {
                dfs(i, j,  0, "");
            }
        }
    }

    return ans;    
};

优化

1. 方向处理：统一方向数组，消除代码冗余

• 原始问题：原始代码通过手动重复调用 dfs(i-1,j,...)、dfs(i+1,j,...) 等4行代码处理上下左右四个方向，代码冗余度高，若需调整方向（如增加对角线），需逐个修改调用语句，维护成本高。
• 优化方案：定义 directions = [[-1,0],[1,0],[0,-1],[0,1]] 数组，用 循环遍历方向（for (const [dx, dy] of directions)）替代重复调用。
• 优化收益：
  • 代码行数减少，可读性提升；
  • 方向逻辑集中管理，修改方向仅需调整数组，灵活性更强。

2. 递归参数：用「索引跟踪」替代「字符串拼接」，降低时间开销

• 原始问题：原始代码通过 s + board[i][j] 拼接字符串，再判断是否等于 word。由于字符串是不可变对象，每次拼接都会生成新字符串，带来额外的内存分配和字符拷贝开销，尤其当 word 较长时，性能损耗明显。
• 优化方案：用 index 参数直接跟踪当前匹配到 word 的索引位置（如 index=2 表示已匹配 word[0] 和 word[1]），只需判断 board[i][j] === word[index] 即可。
• 优化收益：
  • 彻底消除字符串拼接的时间/内存开销；
  • 递归参数从3个（i,j,count,s）简化为2个（i,j,index），参数传递更高效。

3. 返回逻辑：用「布尔值直接返回」替代「全局变量标记」，提前终止递归

• 原始问题：原始代码依赖全局变量 ans 标记是否找到结果，递归中需先判断 ans 是否为 true 再返回，逻辑绕弯；且全局变量可能导致多路径探索时的不必要计算（如已找到结果，仍需完成后续递归栈的回溯）。
• 优化方案：dfs 函数直接返回 布尔值（true 表示当前路径匹配成功，false 表示失败）。一旦某个方向的递归返回 true，立即向上层返回 true，无需继续探索其他方向。
• 优化收益：
  • 逻辑更直观（递归结果直接传递）；
  • 实现「找到即终止」的剪枝效果，减少无效递归，提升搜索效率。

4. 终止条件：合并边界与匹配判断，简化逻辑

• 原始问题：原始代码的终止条件分散（先判断 count >= word.length，再判断 ans 或越界，最后判断字符是否匹配），逻辑分层较乱。
• 优化方案：将「越界、已访问、字符不匹配」三个否定条件合并为一个判断（if (i<0 || i>=m || j<0 || j>=n || visited[i][j] || board[i][j]!==word[index])），与「完全匹配」（index === word.length）共同构成清晰的二元终止逻辑。
• 优化收益：终止条件集中，代码逻辑更紧凑，降低理解成本。

代码二

var exist = function(board, word) {
    const [m, n] = [board.length, board[0].length];
    const visited = Array.from({ length: m }, () => Array(n).fill(false));
    const directions = [[-1, 0], [1, 0], [0, -1], [0, 1]]; // 统一方向数组

    // 递归函数：参数为当前坐标和已匹配到的索引
    const dfs = (i, j, index) => {
        // 终止条件1：所有字符匹配完成
        if (index === word.length) return true;
        // 终止条件2：越界、已访问或当前字符不匹配
        if (i < 0 || i >= m || j < 0 || j >= n || visited[i][j] || board[i][j] !== word[index]) {
            return false;
        }

        // 标记当前位置为已访问
        visited[i][j] = true;

        // 尝试四个方向，只要有一个方向匹配成功就返回true
        for (const [dx, dy] of directions) {
            if (dfs(i + dx, j + dy, index + 1)) {
                return true;
            }
        }

        // 回溯：取消标记
        visited[i][j] = false;
        return false;
    };

    // 遍历所有可能的起点
    for (let i = 0; i < m; i++) {
        for (let j = 0; j < n; j++) {
            // 从第一个字符匹配的位置开始搜索，找到后直接返回
            if (dfs(i, j, 0)) {
                return true;
            }
        }
    }

    return false;
};