【OD机试题解法笔记】构成正方形的数量

题目

输入N个互不相同的二维整数坐标，求这N个坐标可以构成的正方形数量。[内积为零的的两个向量垂直]

输入描述
第一行输入为N，N代表坐标数量，N为正整数。N <= 100

之后的 K 行输入为坐标x y以空格分隔，x，y为整数，-10<=x, y<=10

输出描述
输出可以构成的正方形数量。

用例

输入	输出	说明
3 1 3 2 4 3 1	0	3个点不足以构成正方形
4 0 0 1 2 3 1 2 -1	1

思考

正方形的对角线互相垂直，可以枚举每对坐标为一条对角线，然后旋转90度计算另一条对角线的2个端点坐标，判断计算的2个端点坐标是否存在于已知坐标集中，如果存在则找到一个正方形。由于正方形对角线有两条，枚举每条对角线最终会导致一个正方形被重复枚举2次，最终结果要除以2。

算法过程

1、根据输入把坐标存入List集合中，两重循环遍历List枚举对角线两个端点；

2、根据枚举的两个端点A和B计算AB中点Center和向量V（A或B减去center后把向量长度除以2）；

3、将向量V旋转90度，顺时针或逆时针旋转都行，得到另一个向量V1，通过V1+Center和-V1+Center能计算另一条对角线上的两个端点；

二维旋转

假如我们要把向量 a 逆时针（旋转轴是从笛卡尔坐标系原点指向屏幕外面的轴，这个轴与屏幕垂直）旋转一个角度 φ 得到向量 b，如果 a 与x轴夹角是 α，长度 r = √（x_a^2 + x_b^2)，则 x_a = r cosα, y_a = r sinα；

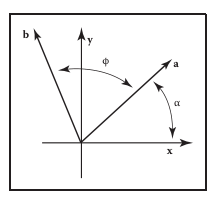
由三角恒等变换得到向量 b的坐标：

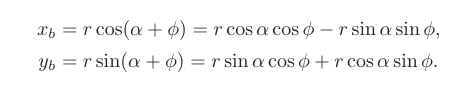
化简后：

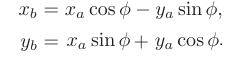
将 a 旋转到得到 b 的转换写成矩阵形式：

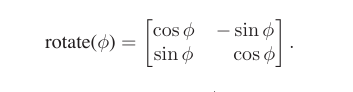
观察旋转矩阵的每行有 sin^2 φ+cos^2 φ = 1，行与行之间存在 cos φ(− sin φ) + sin φ cos φ = 0，从而得到旋转矩阵是标准正交矩阵。旋转矩阵也可以看成一对标准正交的列向量或行向量。

回到题目中，把向量V逆时针旋转90度就是左乘一个旋转矩阵rotate(90):

3、根据AB的中点和向量V1计算端点CD，C = (A + B ) / 2 + V1/2, D = (A + B ) / 2 - V1/2；

4、判断坐标集中是否存在CD，存在则计数+1，最后将结果除以2得到正方形的数量。

参考代码

let cases = [
`3
1 3
2 4
3 1`,
`4
0 0
1 2
3 1
2 -1`
]

let ans = [
  0,
  1
];

let caseIndex = 0;
let lineIndex  = 0;

const readline = (function() {
  let lines = [];
  return function() {
    if (lineIndex === 0) {
      lines = cases[caseIndex].trim().split('\n').map(line => line.trim());
    }
    return lines[lineIndex++];
  }
}());

function solution() {
  const line = readline();
  let n = parseInt(line);
  const coordinates  = [];
  for (let i = 0; i < n; i++) {
    let [x, y] = readline().split(' ').map(e => parseInt(e));
    coordinates.push({x, y});
  }

  let count = 0;
  for (let i = 0; i < n; i++) {
    for (let j = i+1; j < n; j++) {
      let p1 = coordinates[i];
      let p2 = coordinates[j];
      let center = {x : (p1.x + p2.x) / 2, y: (p1.y + p2.y) / 2};
      let v1 = { x: p1.x-center.x, y: p1.y-center.y};
      let v2 = { x: -v1.y, y: v1.x }; // 逆时针旋转90度

      // 另一条对角线的2个端点
      let p3 = { x: center.x + v2.x, y: center.y + v2.y };
      let p4 = { x: center.x - v2.x, y: center.y - v2.y };

      // console.log('p1: ', p1);
      // console.log('p2: ', p2);
      // console.log('center: ', center);
      // console.log('v1: ', v1);
      // console.log('v2: ', v2);
      // console.log('p3: ', p3);
      // console.log('p4: ', p4);
      // console.log('---------------------');
     
      // 判断端点是否存在于已有的坐标集中
      if (coordinates.find(o => o.x === p3.x && o.y === p3.y) 
        && coordinates.find(o => o.x === p4.x && o.y === p4.y)) {
          count++;
       }
    }
  }
 
  // console.log("count = ", count/2);

  return count/2;
}

cases.forEach((_, i) => {
  caseIndex = i;
  lineIndex = 0;

  const result = solution();
  if (result === ans[i]) {
    console.log(true);
  } else {
    console.error(false);
  }
});