目录
为什么要有LSM树
数据库存储引擎索引的底层结构
哈希存储引擎
是哈希表的持久化实现,支持增、删、改以及随机读取操作,但不支持顺序扫描,对应的存储系统为key-value存储系统。
B树存储引擎是B树
不仅支持单条记录的增、删、读、改操作,还支持顺序扫描, 因此B树是传统关系型数据库中索引结构的不二人选。
但从技术角度:由于磁盘的(磁柱、磁盘、磁道、磁头)结构与B树结构的特点,导致传统B树索引存在着随机写效率的上限挑战,所以当在那些索引插入频率远大于查询频率的应用场景下,如历史记录表和日志文件来说,B树索引显得捉襟见肘了。
BTree的随机写特点
一个BTree,对于在没有缓存的Case情况下, 一个随机写分为两步进行:1. 从磁盘Load目标块节点到内存,2.修改它并写回磁盘。所以,BTree在对于随机key值下的平均“blind-write”操作需要两次IO操作,其限定了BTree的随机写吞吐量。
LSM树的诞生背景
传统关系型数据库使用btree或一些变体作为存储结构,能高效进行查找。但保存在磁盘中时它也有一个明显的缺陷,那就是逻辑上相离很近但物理却可能相隔很远,这就可能造成大量的磁盘随机读写。随机读写比顺序读写慢很多,为了提升IO性能,我们需要一种能将随机操作变为顺序操作的机制,于是便有了LSM树。LSM树能让我们进行顺序写磁盘,从而大幅提升写操作,作为代价的是牺牲了一些读性能。
简介
LSM树(Log-Structured MergeTree),日志结构合并树。
LSM树(Log-Structured MergeTree)存储引擎和B+树存储引擎一样,同样支持增、删、读、改、顺序扫描操作。而且通过批量存储技术规避磁盘随机写入问题。当然凡事有利有弊,LSM树和B+树相比,LSM树牺牲了部分读性能,用来大幅提高写性能。
LSM树核心思想的核心就是放弃部分读能力,换取写入的最大化能力。LSM Tree ,这个概念就是结构化合并树的意思,它的核心思路其实非常简单,就是假定内存足够大,因此不需要每次有数据更新就必须将数据写入到磁盘中,而可以先将最新的数据驻留在内存中,等到积累到足够多之后,再使用归并排序的方式将内存内的数据合并追加到磁盘队尾(因为所有待排序的树都是有序的,可以通过合并排序的方式快速合并到一起)。
日志结构的合并树(LSM-tree)是一种基于硬盘的数据结构,与B+tree相比,能显著地减少硬盘磁盘臂的开销,并能在较长的时间提供对文件的高速插入(删除)。然而LSM-tree在某些情况下,特别是在查询需要快速响应时性能不佳。通常LSM-tree适用于索引插入比检索更频繁的应用系统。
LSM树,log-structured,日志结构的,日志是软件系统打出来的,就跟人写日记一样,一页一页往下写,而且系统写日志不会写错,所以不需要更改,只需要在后边追加就好了。各种数据库的写前日志也是追加型的,因此日志结构的基本就指代追加。注意他还是个 “Merge-tree”,也就是“合并-树”,合并就是把多个合成一个。
LSM树与B树的差异
LSM树和B+树的差异主要在于读性能和写性能进行权衡。在牺牲的同时寻找其余补救方案:
(a)LSM具有批量特性,存储延迟。当写读比例很大的时候(写比读多),LSM树相比于B树有更好的性能。因为随着insert操作,为了维护B+树结构,节点分裂。读磁盘的随机读写概率会变大,性能会逐渐减弱。
(b)B树的写入过程:对B树的写入过程是一次原位写入的过程,主要分为两个部分,首先是查找到对应的块的位置,然后将新数据写入到刚才查找到的数据块中,然后再查找到块所对应的磁盘物理位置,将数据写入去。当然,在内存比较充足的时候,因为B树的一部分可以被缓存在内存中,所以查找块的过程有一定概率可以在内存内完成,不过为了表述清晰,我们就假定内存很小,只够存一个B树块大小的数据吧。可以看到,在上面的模式中,需要两次随机寻道(一次查找,一次原位写),才能够完成一次数据的写入,代价还是很高的。
LSM树优化
Bloom filter
就是个带随机概率的bitmap,可以快速的告诉你,某一个小的有序结构里有没有指定的那个数据的。于是就可以不用二分查找,而只需简单的计算几次就能知道数据是否在某个小集合里啦。效率得到了提升,但付出的是空间代价。
compact
小树合并为大树:因为小树性能有问题,所以要有个进程不断地将小树合并到大树上,这样大部分的老数据查询也可以直接使用log2N的方式找到,不需要再进行(N/m)*log2n的查询了
LSM树基本原理
下图是 LSM-tree 的组成部分,是一个多层结构,就更一个树一样,上小下大。首先是内存的 C0 层,保存了所有最近写入的 (k,v),这个内存结构是有序的,并且可以随时原地更新,同时支持随时查询。剩下的 C1 到 Ck 层都在磁盘上,每一层都是一个在 key 上有序的结构。
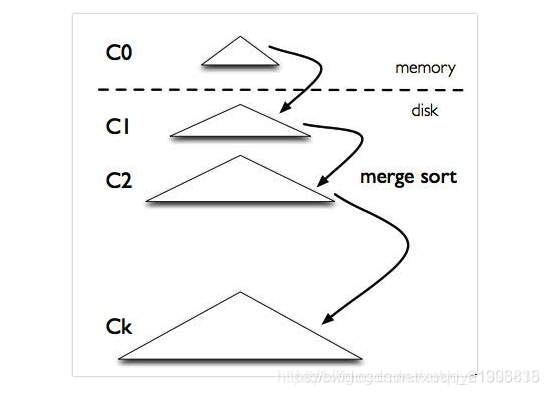
写入流程:一个 put(k,v) 操作来了,首先追加到写前日志(Write Ahead Log,也就是真正写入之前记录的日志)中,接下来加到 C0 层。当 C0 层的数据达到一定大小,就把 C0 层 和 C1 层合并,类似归并排序,这个过程就是Compaction(合并)。合并出来的新的 new-C1 会顺序写磁盘,替换掉原来的 old-C1。当 C1 层达到一定大小,会继续和下层合并。合并之后所有旧文件都可以删掉,留下新的。
注意数据的写入可能重复,新版本需要覆盖老版本。什么叫新版本,我先写(a=1),再写(a=233),233 就是新版本了。假如 a 老版本已经到 Ck 层了,这时候 C0 层来了个新版本,这个时候不会去管底下的文件有没有老版本,老版本的清理是在合并的时候做的。
写入过程基本只用到了内存结构,Compaction 可以后台异步完成,不阻塞写入。
查询流程:在写入流程中可以看到,最新的数据在 C0 层,最老的数据在 Ck 层,所以查询也是先查 C0 层,如果没有要查的 k,再查 C1,逐层查。
一次查询可能需要多次单点查询,稍微慢一些。所以 LSM-tree 主要针对的场景是写密集、少量查询的场景。
LSM-tree 被用在各种键值数据库中,如 LevelDB,RocksDB,还有分布式行式存储数据库 Cassandra 也用了 LSM-tree 的存储架构。
LevelDB中的LSM
下边这个图是 LevelDB 的架构,首先,LSM-tree 被分成三种文件。
第一种是内存中的两个 memtable,一个是正常的接收写入请求的 memtable(灰色的),一个是不可修改的immutable memtable(黑色的)。
另外一部分是磁盘上的 SStable (Sorted String Table)(白色的小方格),有序字符串表,这个有序的字符串就是数据的 key。SStable 一共有七层(L0 到 L6)。下一层的总大小限制是上一层的 10 倍。
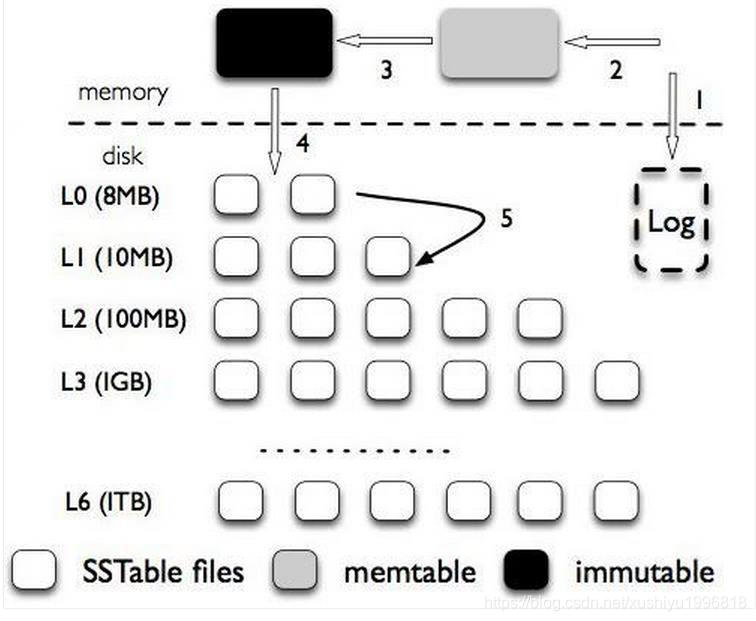
写入流程:首先将写入操作加到写前日志中,接下来把数据写到 memtable中,当 memtable 满了,就将这个 memtable 切换为不可更改的 immutable memtable,并新开一个 memtable 接收新的写入请求。而这个 immutable memtable 就可以刷磁盘了。这里刷磁盘是直接刷成 L0 层的 SSTable 文件,并不直接跟 L0 层的文件合并。
每一层的所有文件总大小是有限制的,每下一层大十倍。一旦某一层的总大小超过阈值了,就选择一个文件和下一层的文件合并。就像玩 2048 一样,每次能触发合并都会触发,这在 2048 里是最爽的,但是在系统里是挺麻烦的事,因为需要倒腾的数据多,但是也不是坏事,因为这样可以加速查询。
这里注意,所有下一层被影响到的文件都会参与 Compaction。合并之后,保证 L1 到 L6 层的每一层的数据都是在 key 上全局有序的。而 L0 层是可以有重叠的。
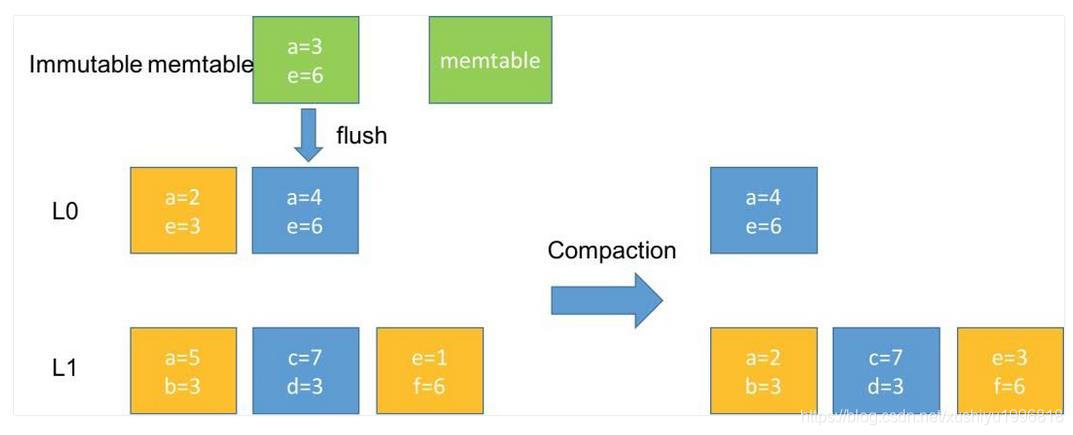
上图是个例子,一个 immutable memtable 刷到 L0 层后,触发 L0 和 L1 的合并,假如黄色的文件是涉及本次合并的,合并后,L0 层的就被删掉了,L1 层的就更新了,L1 层还是全局有序的,三个文件的数据顺序是 abcdef。
虽然 L0 层的多个文件在同一层,但也是有先后关系的,后面的同个 key 的数据也会覆盖前面的。这里怎么区分呢?为每个key-value加个版本号。所以在 Compaction 时候应该只会留下最新的版本。
查询流程:先查memtable,再查 immutable memtable,然后查 L0 层的所有文件,最后一层一层往下查。
LSM-tree读写放大
读写放大(read and write amplification)是 LSM-tree 的主要问题,这么定义的:读写放大 = 磁盘上实际读写的数据量 / 用户需要的数据量。注意是和磁盘交互的数据量才算,这份数据在内存里计算了多少次是不关心的。比如用户本来要写 1KB 数据,结果你在内存里计算了1个小时,最后往磁盘写了 10KB 的数据,写放大就是 10,读也类似。
写放大:我们以 RocksDB 的 Level Style Compaction 机制为例,这种合并机制每次拿上一层的所有文件和下一层合并,下一层大小是上一层的 r 倍。这样单次合并的写放大就是 r 倍,这里是 r 倍还是 r+1 倍跟具体实现有关,我们举个例子。
假如现在有三层,文件大小分别是:9,90,900,r=10。又写了个 1,这时候就会不断合并,1+9=10,10+90=100,100+900=1000。总共写了 10+100+1000。按理来说写放大应该为 1110/1,但是各种论文里不是这么说的,论文里说的是等号右边的比上加号左边的和,也就是10/1 + 100/10 + 1000/100 = 30 = r * level。个人感觉写放大是一个过程,用一个数字衡量不太准确,而且这也只是最坏情况。
读放大:为了查询一个 1KB 的数据。最坏需要读 L0 层的 8 个文件,再读 L1 到 L6 的每一个文件,一共 14 个文件。而每一个文件内部需要读 16KB 的索引,4KB的布隆过滤器,4KB的数据块(看不懂不重要,只要知道从一个SSTable里查一个key,需要读这么多东西就可以了)。一共 24*14/1=336倍。key-value 越小读放大越大。
HBase中的LSM树
LSM树原理把一棵大树拆分成N棵小树,它首先写入内存中,随着小树越来越大,内存中的小树会flush到磁盘中,磁盘中的树定期可以做merge操作,合并成一棵大树,以优化读性能。
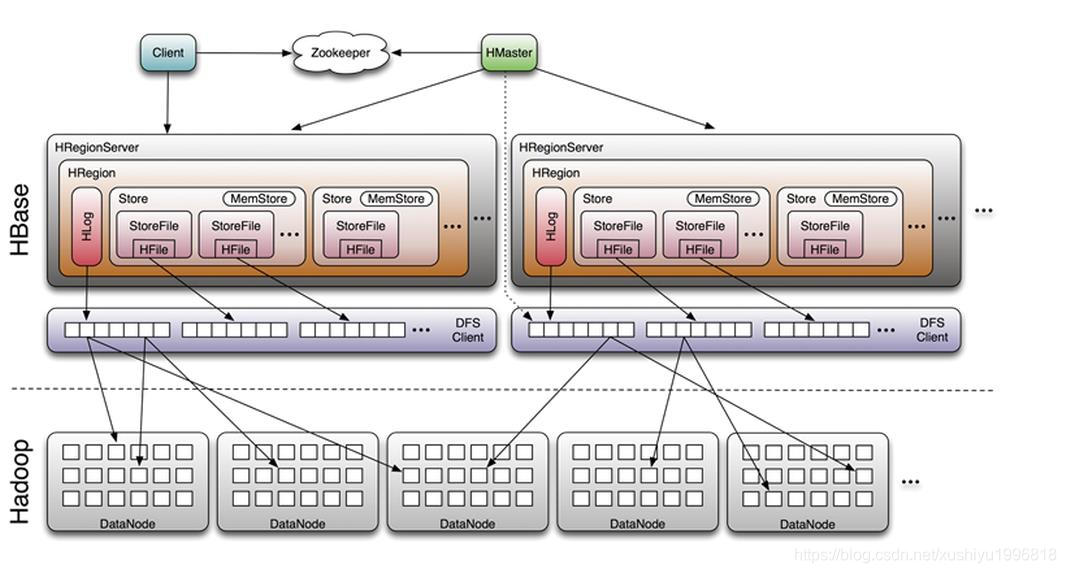
以上这些大概就是HBase存储的设计主要思想,这里分别对应说明下:
因为小树先写到内存中,为了防止内存数据丢失,写内存的同时需要暂时持久化到磁盘,对应了HBase的MemStore(第二层中HRegion下面右面的那个)和HLog(第二层中HRegion下面的那个)
MemStore上的树达到一定大小之后,需要flush到HRegion磁盘中(一般是Hadoop DataNode),这样MemStore就变成了DataNode上的磁盘文件StoreFile(第四层和第二层中store里的东西),定期HRegionServer对DataNode的数据做merge操作,彻底删除无效空间,多棵小树在这个时机合并成大树,来增强读性能。
图解
插入
向LSM树中插入
A E L R U
,首先会插入到内存中的C0树上,这里使用AVL树,插入“A”,先项磁盘日志文件追加记录,然后再插入C0,
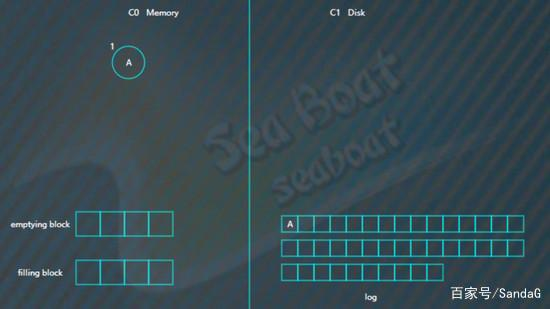
插入“E”,同样先追加日志再写内存,
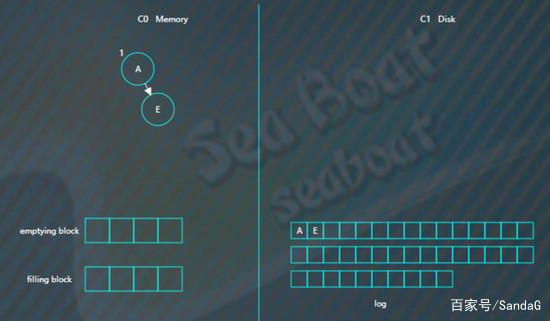
继续插入“L”,旋转后如下,
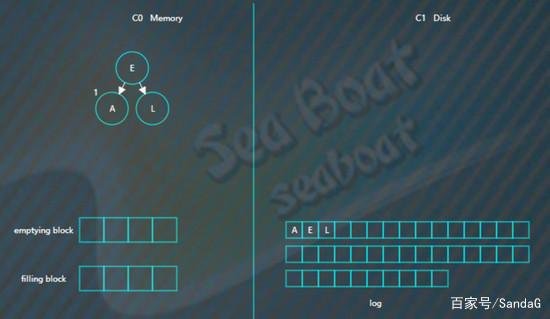
插入“R”“U”,旋转后最终如下。
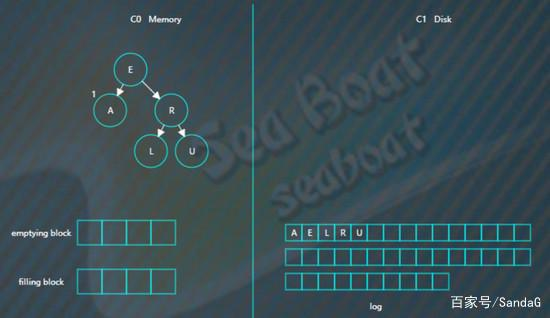
假设此时触发合并,则因为C1还没有树,所以emptying block为空,直接从C0树中依次找最小的节点。filling block长度为4,这里假设磁盘块大小为4。
开始找最小的节点,并放到filling block中,
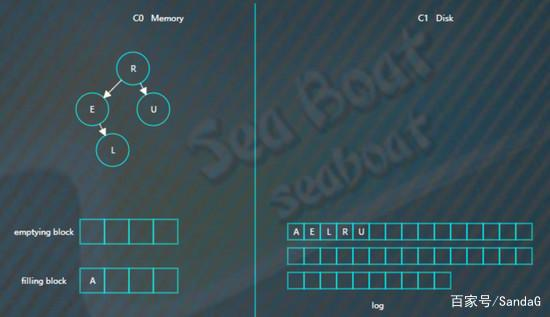
继续找第二个节点,
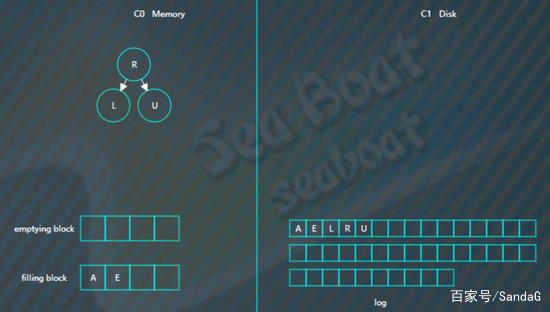
以此类推,填满filling block,
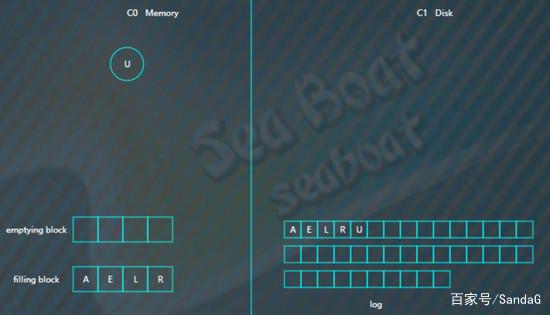
开始写入磁盘,C1树,
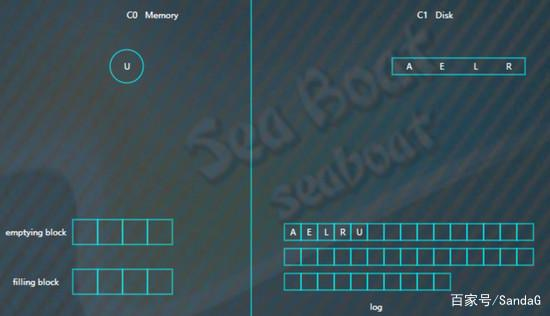
继续插入
B F N T
,先分别写日志,然后插入到内存的C0树中,
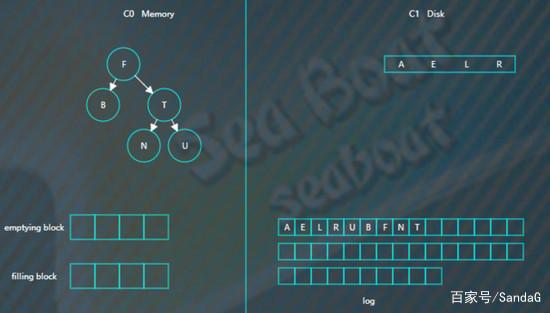
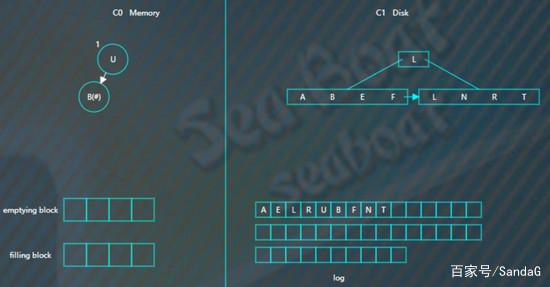
假如此时进行合并,先加载C1的最左边叶子节点到emptying block,
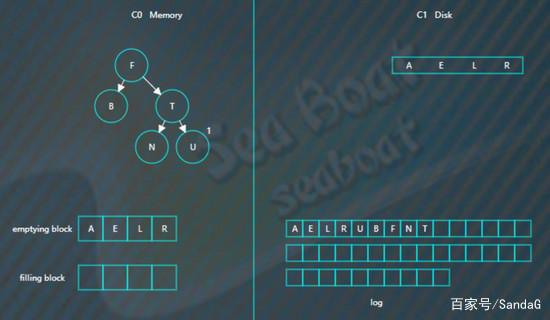
接着对C0树的节点和emptying block进行合并排序,首先是“A”进入filling block,
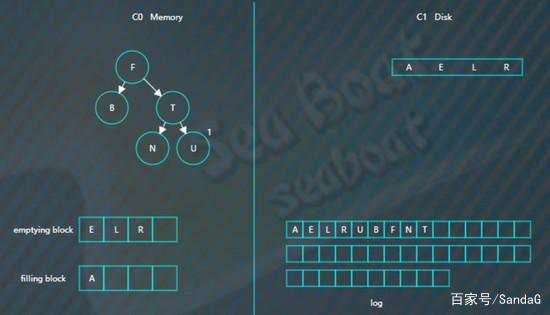
然后是“B”,
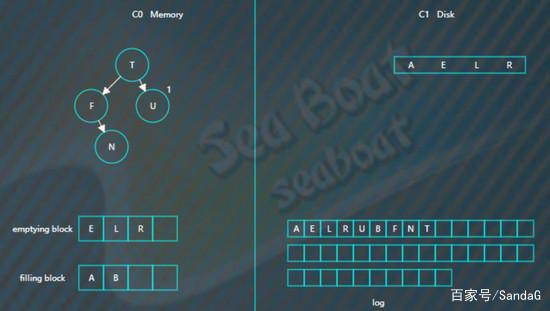
合并排序最终结果为,
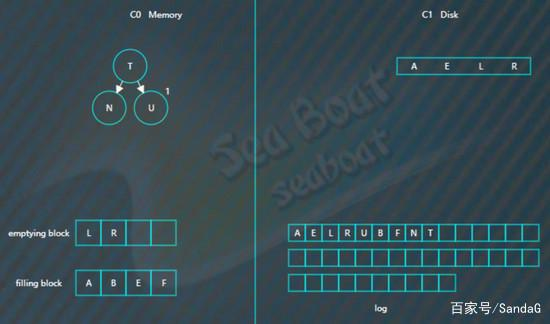
将filling block追加到磁盘的新位置,将原来的节点删除掉,
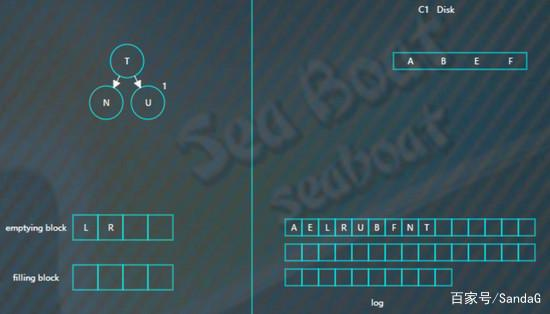
继续合并排序,再次填满filling block,
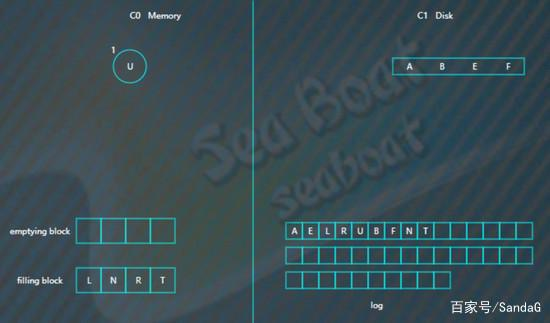
将filling block追加到磁盘的新位置,上一层的节点也要以磁盘块(或多个磁盘块)大小写入,尽量避开随机写。另外由于合并过程可能会导致上层节点的更新,可以暂时保存在内存,后面在适当时机写入。
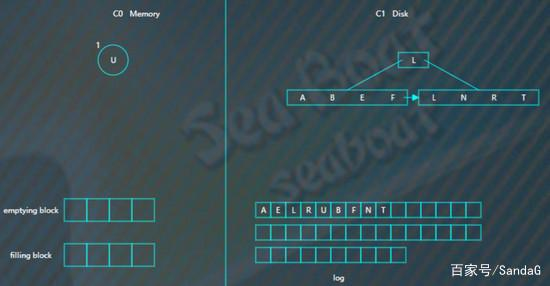
查找
查找总体思想是先找内存的C0树,找不到则找磁盘的C1树,然后是C2树,以此类推。
假如要找“B”,先找C0树,没找到。
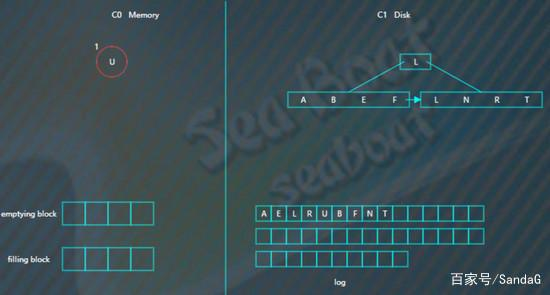
接着找C1树,从根节点开始,
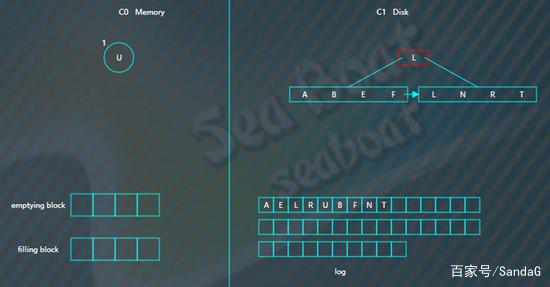
找到“B”。
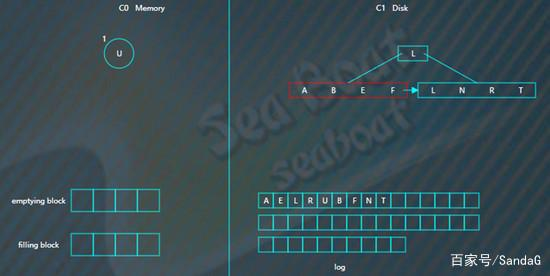
删除
删除操作为了能快速执行,主要是通过标记来实现,在内存中将要删除的记录标记一下,后面异步执行合并时将相应记录删除。
比如要删除“U”,假设标为#的表示删除,则C0树的“U”节点变为,
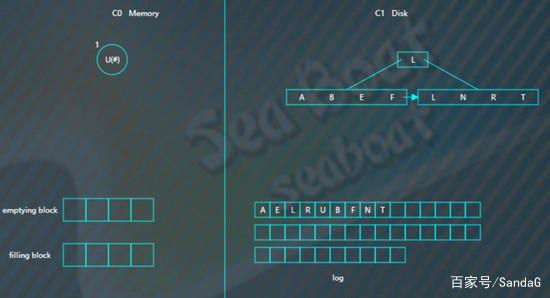
而如果C0树不存在的记录,则在C0树中生成一个节点,并标为#,查找时就能在内存中得知该记录已被删除,无需去磁盘找了。比如要删除“B”,那么没有必要去磁盘执行删除操作,直接在C0树中插入一个“B”节点,并标为#。







 LSM树(Log-Structured Merge Tree)是一种优化随机写入性能的数据结构,常用于数据库存储引擎。与BTree相比,LSM树通过批量存储避免磁盘随机写入,牺牲部分读性能提升写性能。LSM树由多层结构组成,最新数据存储在内存中的C0层,随后通过Compaction过程与磁盘上的层合并。读取时,先查找内存,再逐层向下搜索。LevelDB和HBase等数据库利用LSM树实现高效的存储。写放大和读放大是LSM树的主要问题,影响读写性能。
LSM树(Log-Structured Merge Tree)是一种优化随机写入性能的数据结构,常用于数据库存储引擎。与BTree相比,LSM树通过批量存储避免磁盘随机写入,牺牲部分读性能提升写性能。LSM树由多层结构组成,最新数据存储在内存中的C0层,随后通过Compaction过程与磁盘上的层合并。读取时,先查找内存,再逐层向下搜索。LevelDB和HBase等数据库利用LSM树实现高效的存储。写放大和读放大是LSM树的主要问题,影响读写性能。
















 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








