数据结构（二）

树状关系

什么是树

树（Tree）是n（n≥0）个节点的有限集合T，它满足两个条件 ：
有且仅有一个特定的称为根（Root）的节点；
其余的节点可以分为m（m≥0）个互不相交的有限集合T1、T2、……、Tm，其中每一个集合又是一棵树，并称为其根
的子树（Subtree）。

树有什么特征

什么树度数：
一个节点的子树的个数称为该节点的度数，一棵树的度数是指该树中节点的最大度数
什么是边：什么是路径：
一个节点系列k1,k2, ……,ki,ki+1, ……,kj,并满足ki是ki+1的父节点，就称为一条从k1到kj的路径，路径的
长度为j-1,即路径中的边数。
什么是高度（深度）：
节点的层数等于父节点的层数加一，根节点的层数定义为一。树中节点层数的最大值称为该树的高度或深度。

什么是二叉树？

二叉树的定义 ： 二叉树（Binary Tree）是n（n≥0）个节点的有限集合，它或者是空集（n＝0），或者是由一
个根节点以及两棵互不相交的、分别称为左子树和右子树的二叉树组成。二叉树与普通有序树不同，二叉树严格区
分左孩子和右孩子，即使只有一个子节点也要区分左右。

二叉树的性质

普通的树，转成二叉树

顺序存储

顺序存储太浪费空间，不采用。

链式存储

树结点的定义

结点：包含3个区域： （左孩子）指针域，数据域，（右孩子）指针域
双向链表：
typedef int data_type;
typedef struct bintreenode
{
	struct bintreenode *Left;
	data_type Data;
	struct bintreenode *Right;
}BNode;

//定义数据类型
/*
typedef struct student
{
	char name[20];
	char id[20];
	char add[20];
	int age;
}data_type;*/
//简化操作，将int data_type
typedef int data_type;
//定义链表结点
typedef struct bintreenode
{
	struct bintreenode *Left;
	data_type Data ;
	struct bintreenode *Right;
}BNode;

创建树

创建一个根节点（存数据，不带头结点的链表）

//函数功能：创建结点
//函数参数:void
//函数返回值：成功地址，失败返回NULL
BNode *CreatNode(void)
{
	BNode *pNew = NULL;
	pNew = (BNode *)malloc(sizeof(BNode));
	if(!pNew)
	{
		return NULL;
	}
	memset(pNew, 0, sizeof(BNode));
	return pNew;
}

插入元素（排序二叉树）

本质上，想怎么插入就怎么插入元素
排序二叉树：
左子树的根节点 根节点 右子树的根节点具有某一个关系（升序、降序）

//函数功能：插入元素
//函数参数：被插入元素的树，插入的值，第几次插入
//函数返回值：成功返回OK，失败返回失败原因
int InsertItem(BNode *pTree, data_type item, int *Flag)
{
	BNode *pTmp = pTree;
	BNode *pNew = CreatNode(); //新结点
	//入参判断
	if(!pTree) return LINK_NULL;
	//判断是否是首次插入
	if(*Flag)
	{
		//直接赋值
		pTree->Data = item;
		*Flag = 0; //表明首次插入已完成
		return OK;
	}
	//1.赋值
	pNew->Data = item;
	//找要插入的位置
	while(1)
	{
		if(pNew->Data <= pTmp->Data)
		{
			//往左边找
			if(NULL == pTmp->Left)
			{
				//插入元素
				pTmp->Left = pNew;
				return OK;
			}
			pTmp = pTmp->Left;
		}
		if(pNew->Data > pTmp->Data)
		{
			//右边
			if(NULL == pTmp->Right)
			{
				//插入元素
				pTmp->Right = pNew;
				return OK;
			}
			pTmp = pTmp->Right;
		}
	}
}

访问

先序遍历：
中序遍历：
后序遍历

//函数功能：遍历二叉树
//函数参数：需要遍历的树
//函数返回值：void
void FirTravel(BNode *pTree)
{
	if(!pTree) return ;
	//1、访问根结点
	printf("%d ", pTree->Data);
	//2、以先序便利的方式遍历左子树
	FirTravel(pTree->Left);
	//3、以先序遍历的方式遍历右子树
	FirTravel(pTree->Right);
}
void MidTravel(BNode *pTree)
{
	if(!pTree) return ;
	MidTravel(pTree->Left);
	printf("%d ", pTree->Data);
	MidTravel(pTree->Right);
}
void AftTravel(BNode *pTree)
{
	if(!pTree) return ;
	AftTravel(pTree->Left);
	AftTravel(pTree->Right);
	printf("%d ", pTree->Data);
}

非递归形式：用栈

层次遍历（广度优先）

从上往下，从左往右依次访问结点，使用队列

深度优先

钻进去

平衡二叉树

为了保证查找的效率，避免二叉树降维成类链表形式的存储结构
左、右子树的高度差 < 2

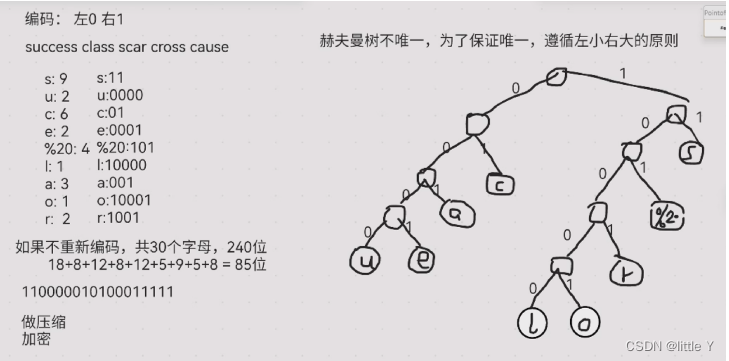
赫夫曼树

又称为最优树，带权路径最小的树

赫夫曼(Huffman)树，又称最优树，是带权路径长度最短的树，有着广泛的应用
从树中一个结点到另外一个结点的分支构成一条路径，分支的数目称为路径的长度。树的路径长度是指从树根到每
个结点的路径长度之和
进一步推广，考虑带权的结点。结点的带权路径长度指的是从树根到该结点的路径长度和结点上权的乘积。树的带
权路径长度是指所有叶子节点的带权路径长度之和，记作 WPL 。WPL最小的二叉树就是最优二叉树，又称为赫夫曼
树

线索二叉树

为了利用起来原来孩子的指针域为空的指针空间（代价，1bit的标志位+重新构建树的时间开销）

堆树

大根堆 和 小根堆：Linux系统里面的定时器
根 >= 左右子结点的值 根 <= 左右子节点的值

红黑树（查找）

1.每个节点非红即黑;
2.根节点是黑的;
3.每个叶节点（叶节点即树尾端NULL指针或NULL节点)都是黑的;
4.如图所示，如果一个节点是红的，那么它的两儿子都是黑的;
5.对于任意节点而言，其到叶子点树NULL指针的每条路径都包含相同数目的黑节点。