大模型必知基础知识：9、MOE多专家大模型底层原理详解

原创已于 2025-10-21 16:52:07 修改 · 893 阅读

28 ·

CC 4.0 BY-SA版权

文章标签：

#人工智能 #大模型应用 #大模型实战 #MOE #LoRAMoE #transformer

于 2025-10-21 07:00:00 首次发布

大模型应用同时被 3 个专栏收录

169 篇文章

订阅专栏

人工智能

145 篇文章

订阅专栏

Transformer

33 篇文章

订阅专栏

大模型必知基础知识：9-MOE多专家大模型底层原理详解

总目录

为什么需要MoE技术
MoE的核心思想与架构设计
- 2.1 MoE的基本组成
- 2.2 MoE在Transformer中的位置
- 2.3 MoE的三大类型
稀疏混合专家模型(Sparse MoE)
- 3.1 稀疏MoE的工作原理
- 3.2 Top-K路由机制
- 3.3 案例：Mixtral-8x7B模型
- 3.4 稀疏MoE的并行计算优势
- 3.5 代表性模型
稠密混合专家模型(Dense MoE)
- 4.1 稠密MoE的特点
- 4.2 与LoRA的结合：LoRAMoE
- 4.3 LoRAMoE的关键设计思想
- 4.4 应用场景与代表模型
软混合专家模型(Soft MoE)
- 5.1 软MoE的折中方案
- 5.2 案例：SMEAR算法
- 5.3 软MoE的优势与权衡
总结

1. 为什么需要MoE技术

就在今年，随着GPT-5、Mixtral-8x7B、DeepSeek-V3、Qwen3等超大规模语言模型的相继问世，特别是国内DeepSeek在国内期间的发布，一种名为混合专家模型(Mixture of Experts, MoE)的技术架构受到学术界和工业界的关注，并且在推理和性能上得到了很大的提升，在加上对比了GPT等模型，得出的能力表现，一发布就感觉给各大模型厂家打开了新大门。
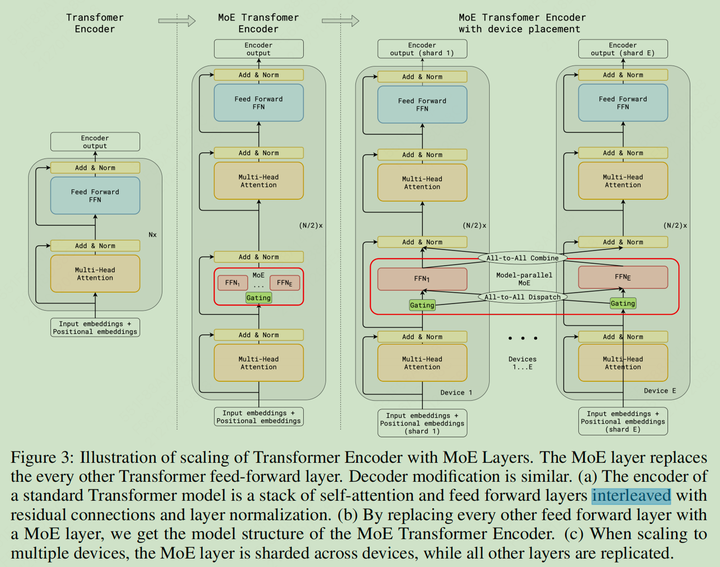
在这里插入图片描述

在人工智能领域，存在一个被广泛验证的规律：模型规模越大，性能表现越好。这就是著名的"大模型缩放定律"(Scaling Law)。

然而，这个规律带来了一个严峻的挑战：当模型参数量从数十亿增长到数千亿甚至数万亿时，所需的算力资源和训练时间会呈指数级增长。

具体来说，训练一个万亿参数级别的模型可能需要数千块GPU持续运行数月之久，其经济成本和能源消耗都是天文数字。对于大多数研究机构和企业而言，这样的资源投入几乎是不可承受的。

因此，一个核心问题浮出水面：在算力资源有限的约束条件下，如何用更少的训练成本和推理开销来支撑起更大规模的模型？

MoE技术为这个问题提供了一个极其巧妙的解决方案。

它的核心思想是：让模型内部的不同模块(称为"专家")各自专注于处理不同类型的任务或数据模式。就像一个大型医院里有心脏科、神经科、骨科等不同科室的医生一样，MoE模型中也有擅长语法分析的专家、擅长逻辑推理的专家、擅长知识记忆的专家等。

更重要的是，当处理一个具体输入时，并不需要所有专家同时工作。系统会通过一个智能的门控网络(Gating Network)来决定应该把输入分配给哪些最合适的专家处理。

可以把门控网络想象成一个智能路由器或调度中心，它能够识别输入的特征，然后将其导向最适合处理该任务的专家。最后，系统会将这些被激活专家的输出结果进行加权组合，得到最终的预测结果。

这种设计带来的好处是显而易见的：模型的总参数规模可以做得非常大(因为有很多专家)，但在实际推理时，每次只需要激活其中一小部分专家参与计算。

这样既保持了大模型的强大能力，又大幅降低了实际的计算开销。正是基于这个原因，MoE架构让拥有数万亿参数的超大规模模型成为可能。例如，Google的Switch Transformers模型达到了惊人的1.6万亿参数量，但其推理效率却远高于同等参数量的稠密模型。

2. MoE的核心思想与架构设计

2.1 MoE的基本组成

一个标准的MoE层通常由两个核心组件构成，它们协同工作来实现条件计算(Conditional Computation)的目标。

第一个组件是专家网络(Expert Networks)。每个专家本质上是一个独立的神经网络模块，通常采用前馈神经网络(Feed-Forward Network, FFN)的结构。在实践中，为了保持架构的一致性和简化实现，每个专家的网络结构往往是相同的，只是参数不同。可以把每个专家理解成一个小型的、专门化的子模型，它们通过训练学习到了处理特定模式数据的能力。

第二个组件是门控网络(Gating Network)，这是MoE架构中最关键的部分。门控网络的作用类似于一个智能的交通指挥系统，它需要完成两个任务：

评估每个专家对当前输入的适配程度，为每个专家计算一个权重分数
根据这些分数决定激活哪些专家，以及如何组合它们的输出

门控网络的数学表达式通常可以写为：

$\text{Softmax}(W_g \cdot x)$

其中， $x$ 是输入向量， $W_g$ 是门控网络的权重矩阵，Softmax函数确保所有专家的权重和为1。

MoE层的最终输出是所有专家输出的加权和：

$\sum_{i=1}^{n} G(x)_i \cdot E_i(x)$

其中， $E_i(x)$ 表示第 $i$ 个专家对输入 $x$ 的输出， $G(x)_i$ 是门控网络分配给第 $i$ 个专家的权重。

2.2 MoE在Transformer中的位置

在现代大语言模型中，MoE层通常被放置在Transformer架构的前馈网络(FFN)部分。这个选择并非偶然，而是有充分的理论和实践依据的。
在这里插入图片描述

研究表明，在大规模Transformer模型中，FFN层的参数量占据了整个模型参数的绝大部分比例。以PaLM模型为例，它拥有5400亿个参数，其中大约90%的参数都集中在FFN层。这意味着FFN层是模型计算的主要瓶颈，也是优化的最佳切入点。

通过将FFN层替换为MoE层，我们可以在保持甚至提升模型容量的同时，显著降低实际的计算开销。具体来说，标准Transformer块的计算流程是：

输入 → 多头自注意力(Multi-Head Attention) → 残差连接与层归一化
→ 前馈网络(FFN) → 残差连接与层归一化 → 输出

而引入MoE后，流程变为：

输入 → 多头自注意力(Multi-Head Attention) → 残差连接与层归一化
→ MoE层 → 残差连接与层归一化 → 输出

这里的MoE层内部包含了门控网络和多个专家FFN的组合。

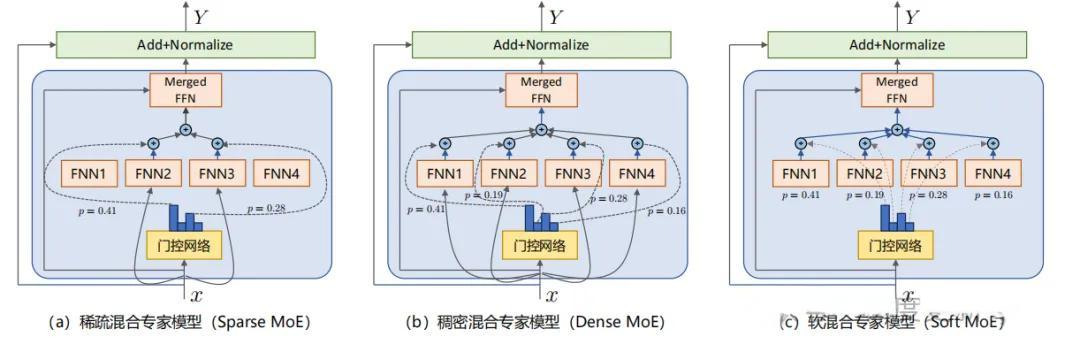
2.3 MoE的三大类型

根据门控机制和专家激活方式的不同，MoE可以分为三种主要类型，每种类型都有其独特的特点和适用场景。

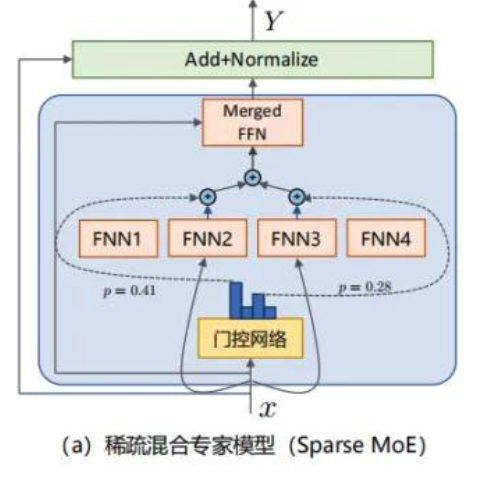
**稀疏MoE(Sparse MoE)**是目前应用最广泛的类型。它的核心特点是每次只激活少数几个专家(通常是1到2个)，其余专家完全不参与计算。这种设计使得模型能够在保持大规模参数量的同时，大幅降低推理时的计算量。稀疏MoE的效率优势非常明显，因此被广泛应用于GPT-4、Mixtral等商业化大模型中。
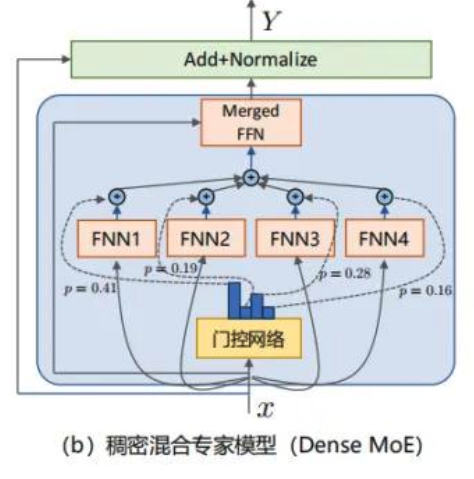
在这里插入图片描述

**稠密MoE(Dense MoE)**则采用了完全不同的策略。它会激活所有专家，只是根据门控网络的权重分配，不同专家的贡献程度不同。虽然这种方式的计算开销较大，但它在模型微调场景中展现出了独特的价值，特别是与参数高效微调技术(如LoRA)结合时。
在这里插入图片描述

**软MoE(Soft MoE)**介于上述两者之间，可以看作是一种折中方案。它不是让每个专家单独计算，而是先将所有专家的参数根据门控权重进行融合，形成一个"虚拟专家"，然后只用这个融合后的网络进行一次计算。这种方式在计算效率和训练稳定性之间取得了较好的平衡。
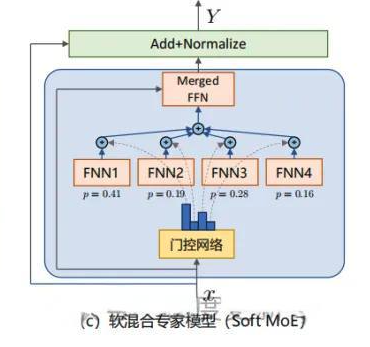
在这里插入图片描述

接下来，我们将详细介绍这三种MoE类型的工作原理、优缺点以及代表性应用。

3. 稀疏混合专家模型(Sparse MoE)

3.1 稀疏MoE的工作原理

稀疏混合专家模型是MoE家族中应用最广泛、效果最显著的一种架构。它的核心设计理念是"按需激活"：对于每一个输入token(比如一句话中的某个词)，模型不需要让所有专家都参与处理，而是通过门控网络智能地选择最合适的少数几个专家来完成计算任务。

这个选择过程可以类比为一个智能的问题分配系统。想象一个大型咨询公司，当客户提出一个技术问题时，公司不会召集所有顾问开会，而是由项目经理(门控网络)评估问题的性质，然后指派最擅长该领域的1到2位专家顾问来解决问题。

从技术实现的角度来看，稀疏MoE的计算流程包含以下步骤：

输入编码：将输入token通过嵌入层转换为向量表示 $x$
门控评分：门控网络计算每个专家的相关性分数 $s_i = W_g \cdot x$
专家选择：选出得分最高的Top-K个专家
专家计算：只让被选中的K个专家对输入进行处理
结果融合：将激活专家的输出进行加权求和

这种设计带来两个关键优势。首先是显著的计算效率提升。由于每次只激活少数专家，实际参与计算的参数量远小于模型的总参数量。其次是专业化的知识分工。不同专家可以专注于学习处理特定类型的模式或任务，这种专业化使得每个专家都能在自己擅长的领域达到更高的性能水平。

3.2 Top-K路由机制

Top-K路由机制是稀疏MoE的核心技术之一。它决定了如何从众多专家中选出最合适的几个来处理当前输入。

在实践中，K值的选择通常是1或2。当K=1时，每个token只由单个专家处理，这带来了最大的计算效率，但可能损失一些表达能力。当K=2时，每个token由两个专家共同处理，这在效率和性能之间取得了较好的平衡，因此在工业界应用更为广泛。

门控网络的输出经过Softmax函数处理后，会为每个专家产生一个概率值。Top-K选择策略会挑选出概率最高的K个专家。数学上，这个过程可以表示为：

$\text{Top-K}(G(x)) = \{i_1, i_2, ..., i_K\} \text{，其中 } G(x)_{i_1} \geq G(x)_{i_2} \geq ... \geq G(x)_{i_K}$

最终的MoE层输出为：

$\sum_{i \in \text{Top-K}(G(x))} \frac{G(x)_i}{\sum_{j \in \text{Top-K}(G(x))} G(x)_j} \cdot E_i(x)$

这里的归一化操作确保了权重和为1。

为了提高训练的稳定性和专家利用率，许多实现会在门控网络的logits中加入可调节的噪声。这个技巧被称为"噪声注入"(Noise Injection)：

$s_i = W_g \cdot x + \epsilon \cdot \text{Noise}$

其中 $\epsilon$ 是一个超参数，Noise通常服从标准正态分布。加入噪声后，不同专家在训练过程中都有机会被激活，避免了某些专家被过度使用而其他专家被闲置的问题。这种机制促进了专家之间的负载均衡，也有助于不同专家学习到更加多样化和互补的知识。

3.3 案例：Mixtral-8x7B模型

Mixtral-8x7B是由Mistral AI公司开发的一个标志性的稀疏MoE模型，它完美展示了稀疏MoE架构在实际应用中的强大能力。

架构设计特点：

Mixtral-8x7B在每个Transformer块中都用稀疏MoE层替代了标准的前馈网络层。具体来说，每个MoE层包含8个专家网络，门控网络会为每个token激活其中的2个专家。这意味着虽然模型总共有8个专家可供选择，但实际计算时只有25%的专家被使用。

在专家网络的内部结构设计上，Mixtral使用了SwiGLU激活函数。SwiGLU是一种改进的门控线性单元(Gated Linear Unit)，其数学形式为：

$\text{SwiGLU}(x) = \text{Swish}(W_1 x) \odot (W_2 x)$

其中 $\odot$ 表示逐元素乘法，Swish是一种平滑的激活函数。SwiGLU已被证明在提升模型表达能力方面非常有效。

与某些MoE实现不同，Mixtral-8x7B没有使用噪声注入机制，而是让门控网络完全通过训练数据学习如何路由。这种设计使得专家的分工更加明确和稳定，但需要更精心的训练策略来避免专家负载不均衡的问题。

参数量与性能：

Mixtral-8x7B的总参数量达到了560亿(8个专家 × 每个专家7B参数)。然而，由于采用了Top-2路由策略，每次前向传播时只有2个专家被激活，因此活跃参数量仅为130亿(2 × 7B + 共享参数)。

这种设计带来了惊人的效率优势。在多个标准基准测试中，Mixtral-8x7B的性能超过了参数量更大的Llama-2-70B(700亿参数的稠密模型)，同时推理速度却快了数倍。这充分证明了稀疏MoE架构在效率和性能之间达到了优秀的平衡。

训练与部署考量：

Mixtral-8x7B的成功也依赖于精心设计的训练策略。模型使用了专家负载均衡损失(Load Balancing Loss)来确保不同专家的利用率相对均匀。这个辅助损失函数会惩罚那些导致某些专家被过度使用的路由决策：

$L_{\text{balance}} = \alpha \cdot \sum_{i=1}^{n} f_i \cdot P_i$

其中 $f_i$ 是专家 $i$ 被选中的频率， $P_i$ 是分配给专家 $i$ 的平均门控概率， $\alpha$ 是平衡系数。

3.4 稀疏MoE的并行计算优势

稀疏MoE架构的另一个重要优势是它天然适合大规模并行计算，这对于在现代GPU集群上高效训练和部署大模型至关重要。

**专家并行(Expert Parallelism)**是MoE模型最常用的并行策略。在这种模式下，不同的专家被分配到不同的GPU设备上。由于稀疏激活的特性，每个token只需要与少数几个GPU通信，大大减少了设备间的数据传输开销。

具体的并行流程如下：

输入数据在所有设备上进行广播或复制
门控网络计算路由决策(可以在单个设备上完成)
根据路由结果，每个token被发送到对应的专家所在的GPU
各GPU上的专家并行处理分配给它们的tokens
计算结果被收集并汇总

与标准的数据并行或模型并行相比，专家并行的通信成本更低，因为不需要在每一层都进行全局同步。

稀疏矩阵计算优化：

研究者们还开发了专门针对MoE的高效计算框架。例如，Megablocks框架将MoE的前馈计算转化为稀疏矩阵乘法操作。传统的MoE实现需要为每个专家单独进行批次计算，这会导致不同专家处理的token数量不均衡，造成计算资源的浪费。

Megablocks通过动态分组和重排技术，将所有需要计算的token重新组织成更高效的批次，然后使用优化的稀疏矩阵乘法内核进行计算。这种方法不仅提升了GPU利用率，还能更好地处理专家负载不均衡的问题。

内存优化策略：

稀疏MoE还可以通过offloading技术来处理超大规模模型。由于每次只激活部分专家，未被激活的专家参数可以暂时存储在CPU内存甚至硬盘上，只在需要时才加载到GPU。这种策略使得在有限的GPU内存下训练和部署更大规模的模型成为可能。

3.5 代表性模型

除了Mixtral-8x7B，稀疏MoE架构还被应用于众多前沿的大语言模型中：

Switch Transformer由Google提出，是早期的大规模稀疏MoE模型之一，最大版本拥有1.6万亿参数，但采用K=1的极端稀疏策略，每次只激活一个专家。

DeepSeek-V3采用了创新的细粒度MoE设计，将专家数量大幅增加，同时减小每个专家的规模，实现了更灵活的专家分工。

Yuan 2.0-M32是浪潮信息发布的中文大模型，采用32个专家的MoE架构，在中文理解任务上表现出色。

Qwen1.5-MoE-A2.7B是阿里云开发的轻量级MoE模型，通过精心设计的专家路由策略，在27亿活跃参数的规模上达到了接近70亿参数稠密模型的性能。

OpenMoE是一个开源的MoE实现框架，为研究者和开发者提供了易于使用的MoE训练和推理工具。

这些模型的成功应用充分证明了稀疏MoE架构在构建高效、可扩展的大语言模型方面的巨大潜力。

4. 稠密混合专家模型(Dense MoE)

4.1 稠密MoE的特点

与稀疏MoE形成鲜明对比的是稠密混合专家模型，它采用了一种截然不同的设计哲学。在稠密MoE中，对于每一个输入token，所有的专家都会被激活并参与计算，门控网络的作用仅仅是为不同专家分配不同的权重。

这种设计可以类比为一个民主决策的委员会。当面临一个问题时，委员会不是选出少数几个成员来做决定，而是让所有成员都发表意见，然后根据每个成员的专业程度和可信度来加权综合这些意见，最终形成集体决策。

稠密MoE的数学表达式为：

$\sum_{i=1}^{n} w_i \cdot E_i(x)$

其中 $w_i = G(x)_i$ 是门控网络为第 $i$ 个专家分配的权重，所有权重的和为1。与稀疏MoE不同的是，这里所有的 $w_i$ 都是非零值，所有专家都会对最终输出做出贡献。

计算开销分析：

显而易见，稠密MoE的最大缺点是计算成本高昂。如果有 $n$ 个专家，那么每个token都需要进行 $n$ 次完整的专家网络计算。这意味着计算量是单个FFN层的 $n$ 倍，在参数量相同的情况下，稠密MoE的推理速度会远慢于稀疏MoE。

正是由于这个根本性的效率劣势，稠密MoE在大规模预训练阶段很少被采用。然而，研究者们发现，在模型微调场景下，稠密MoE展现出了独特的价值，特别是当与参数高效微调技术结合使用时。

4.2 与LoRA的结合：LoRAMoE

LoRA(Low-Rank Adaptation)是一种流行的参数高效微调技术。它的核心思想是在预训练模型的权重矩阵旁边添加低秩分解矩阵作为可训练参数，而保持原始模型权重冻结不变。
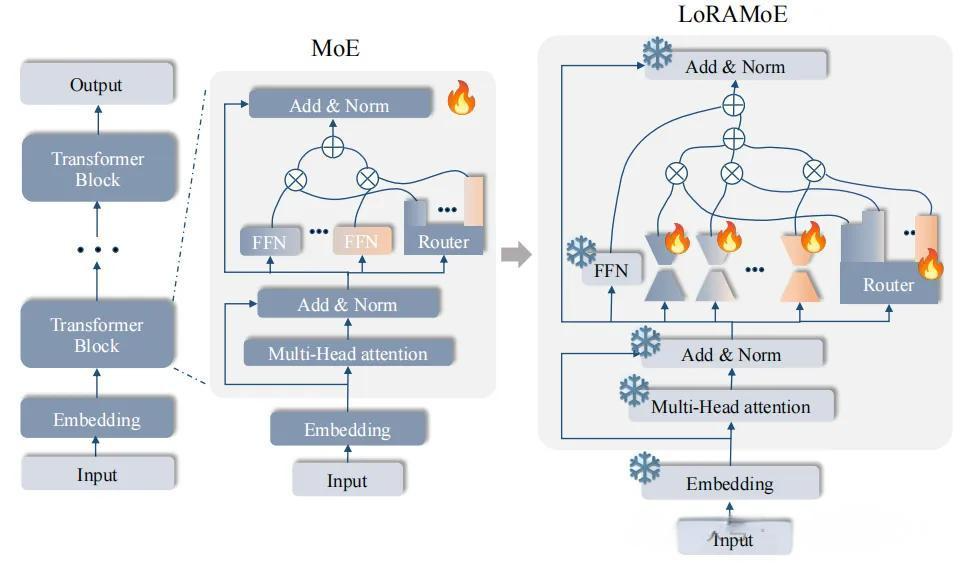
在这里插入图片描述

对于一个权重矩阵 $\in \mathbb{R}^{d \times k}$ ，LoRA会添加一个更新项：

$W^{'} = W + B A$

其中 $\in \mathbb{R}^{d \times r}$ ， $\in \mathbb{R}^{r \times k}$ ，并且秩 $\ll \min(d, k)$ 。只有 $A$ 和 $B$ 是可训练的，而 $W$ 保持冻结。

LoRAMoE将LoRA和MoE这两种技术巧妙地结合在一起，形成了一种特别适合下游任务微调的架构。这种结合解决了一个长期困扰大模型微调的矛盾问题：如何在提升特定任务性能的同时，保持模型原有的通用知识和能力。

4.3 LoRAMoE的关键设计思想

LoRAMoE的架构设计体现了几个重要的设计原则，每个原则都针对微调过程中的特定挑战。

插件化设计与知识保护：

LoRAMoE将LoRA适配器以插件的形式加入到模型中。在训练过程中，主模型的参数完全冻结，所有的梯度更新都集中在LoRA插件上。这种设计带来了关键的好处：预训练阶段学习到的世界知识和常识被完整地保留下来，不会因为在特定任务上的微调而被破坏或遗忘。

用公式表示，对于模型的前馈层：

$\text{FFN}(x) = W_2 \cdot \sigma(W_1 \cdot x)$

LoRAMoE会将其扩展为：

$\text{LoRAMoE}(x) = W_2 \cdot \sigma(W_1 \cdot x) + \sum_{i=1}^{n} w_i \cdot [B_i^{(2)} A_i^{(2)} \cdot \sigma(B_i^{(1)} A_i^{(1)} \cdot x)]$

这里第一项是冻结的原始FFN，第二项是MoE形式的LoRA适配器集合。

专家功能分工：

LoRAMoE在模型的前馈网络旁边增加多个专家，这些专家通过门控网络与主模型连接。关键的创新在于专家的功能定位：

任务专家(Task Experts)：这类专家专注于提升下游任务的性能。它们学习任务特定的模式和知识，例如在情感分析任务中学习情感词汇的表示，在问答任务中学习推理模式。
知识保持专家(Knowledge Retention Experts)：这类专家的职责是维护指令遵循能力和世界知识的一致性。它们通过在通用语料上的持续训练，确保模型不会因为专注于特定任务而失去通用能力。

这种双轨制的专家设计使得模型能够在专业化和通用化之间取得平衡。

局部平衡约束(Local Balance Constraint)：

为了避免某些专家"独占舞台"而其他专家被闲置，LoRAMoE引入了局部平衡约束机制。这个机制通过一个辅助损失函数来实现：

$local_balance = λ ⋅ Var ( { ∑ x ∈ B w i ( x ) ∣ i = 1 , . . . , n } ) L_{\text{local\_balance}} = \lambda \cdot \text{Var}(\{\sum_{x \in B} w_i(x) | i = 1, ..., n\})$

其中 $B$ 是一个小批次的训练样本， $\text{Var}$ 表示方差操作。这个损失项惩罚专家负载分布的不均衡性，鼓励门控网络将不同的输入样本分配给不同的专家，从而让所有专家都得到充分训练和利用。

路由策略优化：

LoRAMoE的门控网络不仅考虑当前输入与专家的匹配度，还会考虑专家的历史负载情况。通过动态调整门控权重，系统可以实现更智能的负载均衡。具体来说，如果某个专家在最近的若干步中被频繁激活，门控网络会降低它被继续选中的概率，从而给其他专家更多的学习机会。

4.4 应用场景与代表模型

稠密MoE和LoRAMoE特别适合以下几种应用场景：

多任务学习：当需要在一个模型中同时支持多个不同的下游任务时，可以为每个任务或任务类别训练专门的专家。门控网络会自动学习如何根据输入的特征将其路由到最合适的任务专家。

持续学习：在不断加入新任务的场景下，可以通过增加新的专家来学习新知识，而不需要重新训练整个模型。旧的专家保持冻结，从而避免了灾难性遗忘问题。

领域适应：当需要将通用模型适配到特定领域时，可以通过添加领域专家来增强模型在该领域的能力，同时保持在其他领域的性能。

代表性的稠密MoE模型包括：

MoLE(Mixture of LoRA Experts)：这是早期将LoRA与MoE结合的尝试，验证了这种组合在多任务学习中的有效性。

DS-MoE(Domain-Specific MoE)：针对不同专业领域设计专门的专家，在医疗、法律、金融等垂直领域取得了良好效果。

EvoMoE(Evolutionary MoE)：采用进化算法来优化专家的配置和门控策略，实现了更灵活的专家组合方式。

虽然稠密MoE在计算效率上不如稀疏MoE，但其在特定场景下展现出的优势使其成为模型微调和多任务学习的重要工具。

5. 软混合专家模型(Soft MoE)

5.1 软MoE的折中方案

软混合专家模型(Soft MoE)是MoE家族中的一个创新设计，它在稀疏MoE和稠密MoE之间寻找了一个巧妙的平衡点。软MoE的核心思想是：不让专家单独计算，而是先将所有专家的参数按照门控权重进行融合，形成一个"虚拟专家"，然后只用这个融合后的网络进行一次前馈计算。

这个设计可以类比为团队协作中的"集体智慧"模式。不是让每个专家独立完成整个任务然后再综合结果，而是先让所有专家共同讨论、形成一个统一的方案，然后按照这个方案执行一次。

数学表达：

假设有 $n$ 个专家，每个专家的权重矩阵为 $W_i^{(1)}$ 和 $W_i^{(2)}$ ，门控网络输出的权重为 $w_1, w_2, ..., w_n$ 。软MoE的计算过程为：

首先融合所有专家的参数：

$W_{\text{fused}}^{(1)} = \sum_{i=1}^{n} w_i \cdot W_i^{(1)}$

$W_{\text{fused}}^{(2)} = \sum_{i=1}^{n} w_i \cdot W_i^{(2)}$

然后使用融合后的权重进行一次前馈计算：

$W_{\text{fused}}^{(2)} \cdot \sigma(W_{\text{fused}}^{(1)} \cdot x)$

优势分析：

软MoE相比于稠密MoE的关键优势在于计算效率。稠密MoE需要对每个专家都执行完整的前馈计算，然后再加权求和，计算量是 $\cdot d^2)$ (其中 $n$ 是专家数量， $d$ 是隐藏层维度)。而软MoE先融合参数再计算，只需要一次前馈传播，计算量是 $\cdot d + d^2)$ 。当 $d$ 较大时(在大模型中通常是数千甚至上万)，软MoE的计算开销接近于单个FFN层。

相比于稀疏MoE，软MoE的优势在于训练的稳定性。稀疏MoE中的Top-K选择操作是不可微的，需要使用各种技巧(如Gumbel-Softmax)来近似梯度。而软MoE的所有操作都是完全可微的，梯度可以顺畅地流向所有专家，使得训练过程更加稳定和高效。

5.2 案例：SMEAR算法

SMEAR(Soft Mixture of Experts with Adaptive Routing)是一个代表性的软MoE实现，它展示了软MoE架构的实际应用效果。

核心设计：

SMEAR算法采用了自适应的门控机制，门控网络不仅考虑输入特征，还会动态调整融合的粒度。具体来说：

分层融合：SMEAR不是简单地对所有专家参数进行加权平均，而是采用分层融合策略。首先将专家分组，在组内进行细粒度融合，然后在组间进行粗粒度融合。这种层次化的设计使得模型能够更灵活地捕捉不同尺度的专家协作模式。
自适应权重：门控网络会根据输入的复杂度动态调整融合权重的分布。对于简单的输入，权重分布会更加集中，接近稀疏MoE的效果；对于复杂的输入，权重分布会更加均匀，充分利用所有专家的知识。
正则化约束：为了避免权重过于集中导致某些专家从未被有效利用，SMEAR引入了熵正则化：

$L_{\text{entropy}} = -\beta \cdot \sum_{i=1}^{n} w_i \log w_i$

这个损失项鼓励门控网络产生更加分散的权重分布，确保所有专家都能得到适当的训练。

性能表现：

在多个基准测试中，SMEAR展现出了优异的性能。在相同的参数量和训练数据下，SMEAR的性能接近稠密MoE，但推理速度快了约3到5倍。与稀疏MoE相比，SMEAR在某些需要综合多方面知识的复杂任务上表现更好，因为它能够同时利用所有专家的知识。

内存优化：

SMEAR还实现了一种巧妙的内存优化策略。由于参数融合操作可以提前离线完成，在推理时可以只保存融合后的权重，而不需要存储所有专家的原始参数。这使得部署时的内存占用大大降低。具体来说，如果门控权重在推理时保持相对稳定，可以预先计算好几个常用的融合配置，在运行时根据输入快速选择最合适的配置。

5.3 软MoE的优势与权衡

优势总结：

计算效率：软MoE的计算开销接近单个FFN层，远低于稠密MoE，同时避免了稀疏MoE的路由开销和负载不均衡问题。
训练稳定性：完全可微的架构使得梯度反传更加稳定，不需要复杂的训练技巧，收敛速度通常快于稀疏MoE。
知识融合：通过参数层面的融合，软MoE能够更好地整合不同专家的知识，在需要综合判断的任务上表现出色。
部署友好：可以通过预计算和缓存来进一步优化推理性能，在资源受限的环境下部署更加容易。

权衡考虑：

参数融合开销：虽然前馈计算只需要一次，但参数融合本身也需要计算时间。当专家数量很多或参数维度很大时，融合操作的开销不可忽略。不过，这个开销可以通过并行计算或预计算来缓解。
专家专业化程度：由于所有专家的输出都会被融合，软MoE中的专家专业化程度可能不如稀疏MoE那么明显。每个专家更像是学习某种"倾向"或"偏好"，而不是完全专注于某类特定任务。
可解释性：参数融合使得追踪特定专家的贡献变得困难，不如稀疏MoE那样可以清楚地看到哪些专家被激活了。

应用场景建议：

软MoE特别适合以下场景：