多重集组合数

题目: 有n种物品, 第i种物品有a个. 不同种类的物品可以互相区分, 但相同种类的无法区分.

从这些物品中取出m个, 有多少种取法? 求出数模M的余数.

例如: 有n=3种物品, 每种a={1,2,3}个, 取出m=3个, 取法result=6(0+0+3, 0+1+2, 0+2+1, 1+0+2, 1+1+1, 1+2+0).

题目来自挑战程序设计竞赛P68页

我是蒟蒻，想了一天，才理清思路，给各位大佬分享下，忘指点！

首先上AC代码：

#include<iostream>
#include<cstdlib>
using namespace std;
int dp[1010][1010];
int main(){
    int n,m,a[1010];
    cin>>n>>m;
    for(int i=0;i<n;i++)
        cin>>a[i];//输入每个物品的数量 
    for(int i=0;i<n+2;i++)
        dp[i][0]=1;//不论有多少种物品，当分配数为0时，就只有一种方案 
    for(int i=0;i<n;i++)//核心代码
        for(int j=1;j<=m;j++)
            if(j>=a[i])   dp[i+1][j]=dp[i+1][j-1]+dp[i][j]-dp[i][j-1-a[i]];
            else dp[i+1][j]=dp[i+1][j-1]+dp[i][j];
    cout<<dp[n][m];
    system("PAUSE");
}

树上思路讲的很模糊，我就来理理

 核心代码讲解：
    我的dp状态是怎么得出来的呢？
    

for(int i=0;i<n;i++)
            for(int j=1;j<=m;j++)
                for(int k=1;k<=a[i];k++)
                    dp[i+1][j]+=dp[i][j-k];
//从第i种商品取出来k个，方案数i-1种每个j-k重量的方案和（在纸上自己推一下）     

但是这种写法，，，，O(nmm)复杂度。

即 有：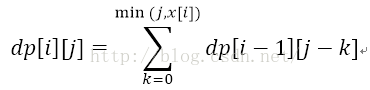  

把最内的循环节俭下来得到一个公式：

分两种情况：

 

情况1：j<=x[i]  （即j-1<x[i]）

右边展开得到的是dp[i][0] dp[i][1] dp[i][2]....dp[i][j] 、 把最后一项拿出来，剩下的j-1项求和，但是我们写成这样：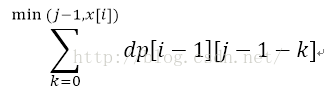

，与原来等价，且我们能轻易发现，这就是dp[i][j-1];

也就是 dp[i][j]=dp[i][j-1]+dp[i-1][j];

情况 2：  j>x[i]

 

右边展开得到的是dp[i][j-x[i]] dp[i][j-x[i]+1] dp[i][j-x[i]+2]....dp[i][j] 、仿照上面的形式，同样得到一个求和式（上界取x[i]），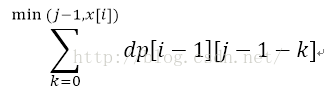

显然能发现这个式子拆开后，多出一项dp[i][j-1-x[i]]，所以最后要减掉，即：dp[i][j]=dp[i][j-1]+dp[i-1][j] - dp[i][j-1-x[i]];