LeetCode 热题 HOT 100 - 206. 反转链表

最新推荐文章于 2025-12-03 23:35:37 发布

原创最新推荐文章于 2025-12-03 23:35:37 发布 · 284 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#leetcode

算法专栏收录该内容

23 篇文章

订阅专栏

本文对比了两种方法：迭代和递归，详细介绍了如何在O(n)时间复杂度下反转单链表。两种方法的空间复杂度分别为O(1)和O(n)，展示了链表反转的经典问题及其解决方案。

思路1：迭代

初始：

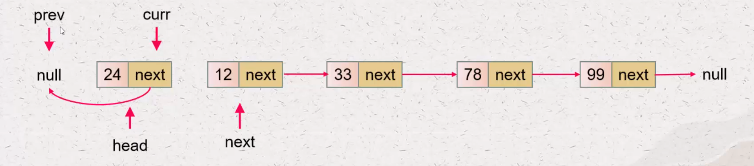
——时间复杂度：O(n)，其中 n 是链表的长度。需要遍历链表一次。

——空间复杂度：O(1)。

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode reverseList(ListNode head) {
        ListNode prev = null;
        ListNode curr = head;
        while (curr != null) {
            ListNode next = curr.next;
            curr.next = prev;
            prev = curr;
            curr = next;
        }
        return prev;
    }
}

思路2：递归

链表具有天然的递归性质！反转单链表可以使用递归实现：符合递归编程的三个条件！

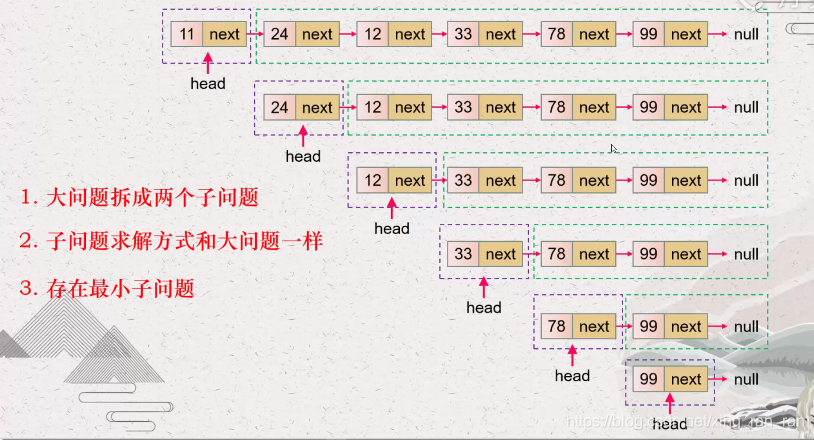
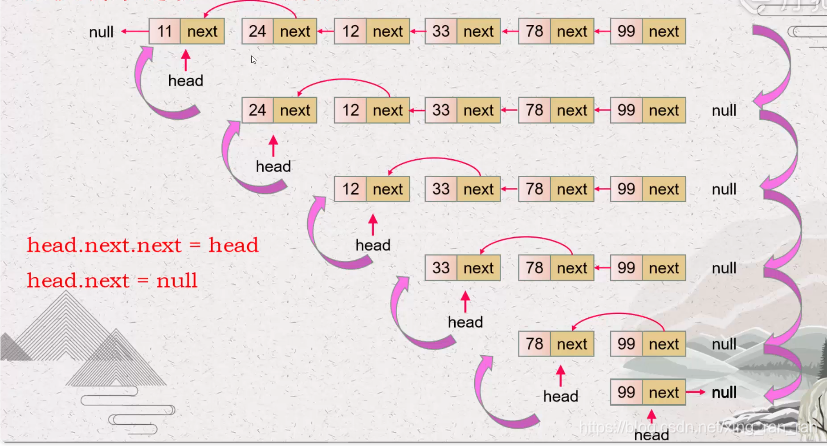
——时间复杂度：O(n)，其中 n 是链表的长度。需要对链表的每个节点进行反转操作。

——空间复杂度：O(n)，其中 n 是链表的长度。空间复杂度主要取决于递归调用的栈空间，最多为 n 层。

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode reverseList(ListNode head) {
        //递归终止条件
        if (head == null || head.next == null) {
            return head;
        }
        ListNode p = reverseList(head.next);
        head.next.next = head;
        head.next = null;
        return p;
    }
}