LeetCode 热题 HOT 100 - 155. 最小栈

最新推荐文章于 2025-09-03 23:35:26 发布

原创最新推荐文章于 2025-09-03 23:35:26 发布 · 228 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#leetcode

算法专栏收录该内容

23 篇文章

订阅专栏

本文介绍了一种利用辅助栈实现的最小值栈，保证了push、pop、top和getMin操作的时间复杂度均为O(1)。进阶讨论了如何在不使用额外空间的情况下，通过存储与最小值的差值来达到相同效果，但需处理可能出现的整数边界问题。

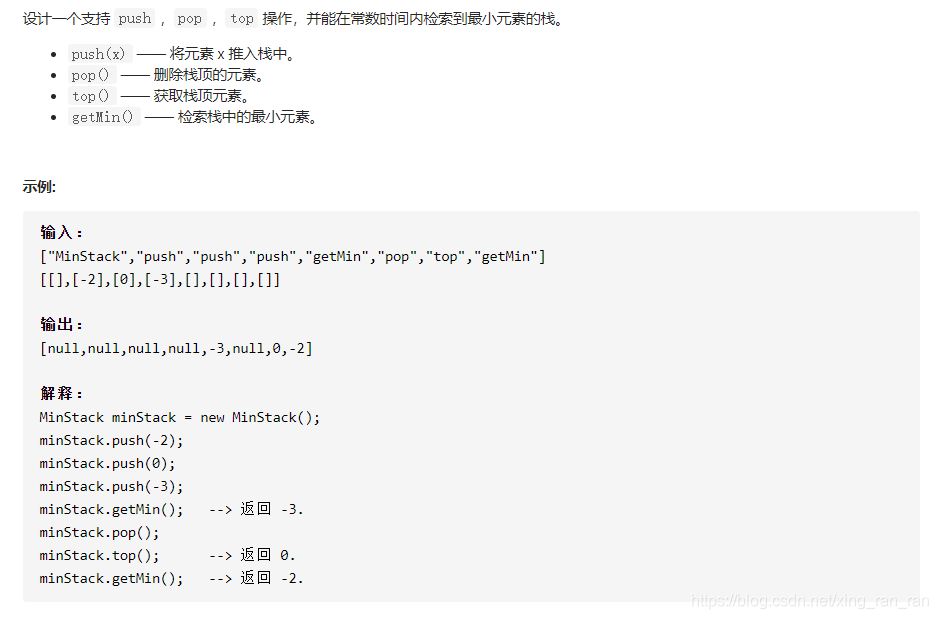
思路：辅助栈

1）初始化数据栈和辅助栈 2）push操作时，首先将元素压入数据栈，需要保持辅助栈的栈顶为最小值，如果当前元素是当前最小值需要压入辅助栈 3）pop操作时，首先删除数据栈的栈顶元素，若该元素是当前的最小值，也需要删除辅助栈的栈顶元素 4）top操作时，返回数据栈的栈顶元素 5）getMin操作时，返回辅助栈的栈顶元素

——时间复杂度：对于题目中的所有操作，时间复杂度均为 O(1)。因为栈的插入、删除与读取操作都是 O(1)，我们定义的每个操作最多调用栈操作两次。

——空间复杂度：O(n)，其中 n 为总操作数。最坏情况下，我们会连续插入 n 个元素，此时两个栈占用的空间为 O(n)。

class MinStack {

    /** initialize your data structure here. */
    private Stack<Integer> dataStack;
    private Stack<Integer> minStack;

    public MinStack() {
        dataStack = new Stack<>();
        minStack = new Stack<>();
    }
    
    public void push(int x) {
        dataStack.push(x);
        if(minStack.isEmpty() || x <= minStack.peek()){
            minStack.push(x);
        }
    }
    
    public void pop() {
        int x = dataStack.pop();
        if(x == minStack.peek()){
            minStack.pop();
        }
    }
    
    public int top() {
        return dataStack.peek();
    }
    
    public int getMin() {
        return minStack.peek();  
    }
}

/**
 * Your MinStack object will be instantiated and called as such:
 * MinStack obj = new MinStack();
 * obj.push(x);
 * obj.pop();
 * int param_3 = obj.top();
 * int param_4 = obj.getMin();
 */

进阶：不用额外空间的做法？思路是栈里保存差值。

只需要一个stack，stack中存的是与min的差值，但由于min是两个整数之间的差值，有可能会出现差值超过整数边界值的情况，因此要变成Long型

参见https://blog.youkuaiyun.com/smileAi66/article/details/108381527