狄克斯特拉算法
广度优先搜索是找出最短的路径,而狄克斯特拉算法是找出最快的路径。
广度优先搜索来查找两点之间的最短路径,那时“最短路径”的意思是段数最少。在狄克斯特拉算法中,你给每段都分配了一个数字或权重,因此狄克斯特拉算法找出的是总权重最小的路径。如下图所示: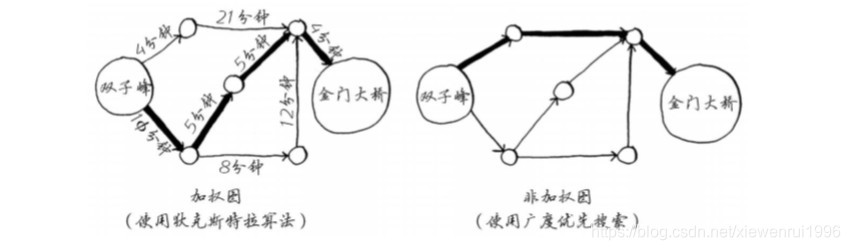
狄克斯特拉算法包含下面4个步骤:
(1) 找出最便宜的节点,即可在最短时间内前往的节点
(2) 对于该节点的邻居,检查是否有前往它们的更短路径,如果有,就更新其开销。
(3) 重复这个过程,直到对图中的每个节点都这样做了。
(4) 计算最终路径。
计算非加权图的最短路径可以使用广度优先搜索,计算加权图最短路径使用狄克斯特拉算法。狄克斯特拉算法只适用于有向无环图。
PS:不能将狄克斯特拉算法用于包含负权边的图。在包含负权边的图中,要找出最短路径,可使用另一种算法——贝尔曼福德算法(Bellman-Ford algorithm)
狄克斯特拉算法实现:
#创建图表
graph={}
graph["start"]={}
graph["start"]["a"]=6 #表示边的权重
graph["start"]["b"]=2
#下面添加其他节点及邻居
graph["a"]={}
graph["a"]["fin"]=1
graph["b"]={}
graph["b"]["a"]=3
graph["b"]["fin"]=5
graph["fin"]={} #终点没有任何邻居
#需要一个散列表来储存每个节点的开销,对于还不知道的开销,你可以设置为无穷大
infinity=float("inf")
costs={}
costs["a"]=6
costs["b"]=2
costs["fin"]=infinity
#创建一个储存父节点的散列表
parents{}
parents["a"]="start"
parents["b"]="start"
parents["fin"]=None
#创建一个记录处理过节点的散列表
processed={}
#定义一个找出最小开销的节点
def find_lowest_cost_node(costs):
lowest_cost=float("inf")
lowest_cost_node=None
for node in costs: #遍历所有节点
cost=costs[node]
if cost < lowest_cost_node and node not in processed: #如果
当前的节点开销更低且未处理
lowest_cost=cost #就将其视为开销最低的节点 lowest_cost_node=node
return node
node=find_lowest_cost_node(costs)
while node is not None:
cost=costs[node]
neighbors=graph[node]
for n in neighbors.keys(): #遍历当前节点的所有邻居
new_cost=cost+neighbors[n]
if costs[n]>new_cost: #如果当前节点前往该邻居更近
costs[n]=new_cost #就更新该邻居的开销
parents[n]=node #同时将该邻居的父节点设置为当前节点
processed.append(node) #将当前节点标记为处理过
node=find_lowest_cost_node(costs) #找出接下来要处理的节点并循环
贪婪算法
用专业术语说,贪婪算法就是你每步都选择局部最优解,最终得到的就是全局最优解。但是贪婪策略有时候不能获得最优解,只能接近最优解。下例为集合覆盖问题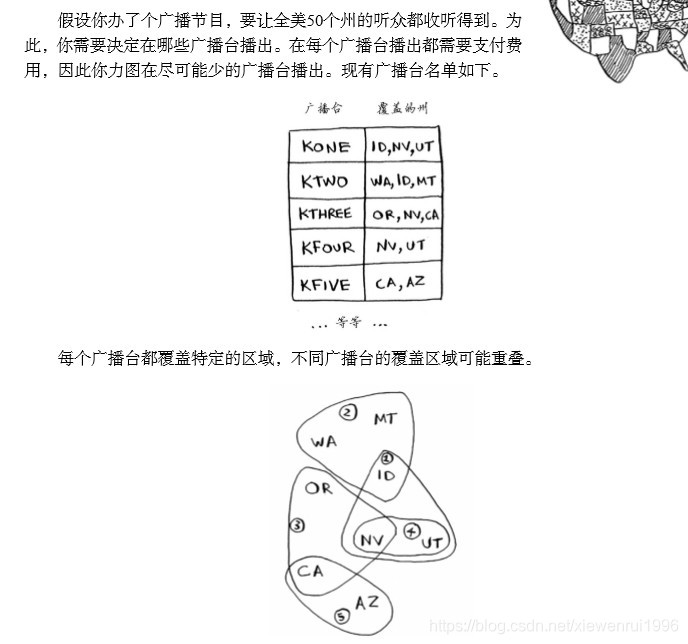
上述问题没有任何算法可以足够快的解决它,因此可以用贪婪算法化解。步骤如下:
(1) 选出这样一个广播台,即它覆盖了最多的未覆盖州。即便这个广播台覆盖了一些已覆盖 的州,也没有关系。
(2) 重复第一步,直到覆盖了所有的州。
下面为代码:
states_needed = set(["mt", "wa", "or", "id", "nv", "ut", "ca", "az"]) //传入一个数组,他被转化为集合
//还需要有可供选择的广播台清单,我选择使用散列表来表示它
stations = {}
stations["kone"] = set(["id", "nv", "ut"])
stations["ktwo"] = set(["wa", "id", "mt"])
stations["kthree"] = set(["or", "nv", "ca"])
stations["kfour"] = set(["nv", "ut"])
stations["kfive"] = set(["ca", "az"])
//最后,需要使用一个集合来存储最终选择的广播台。
final_stations = set()
//不断循环,直到states_needed为空
while states_needed:
best_station = None
states_covered = set() 包含广播台覆盖的所有未覆盖的州
for station, states in stations.items():
covered = states_needed & states
if len(covered) > len(states_covered):
best_station = station
states_covered = covered
states_needed -= states_covered
final_stations.add(best_station)
NP完全问题
旅行商问题:路线为n!一般没有算法可以快速解决
如何识别NP完全问题:
元素较少时算法的运行速度非常快,但随着元素数量的增加,速度会变得非常慢。
涉及“所有组合”的问题通常是NP完全问题。
不能将问题分成小问题,必须考虑各种可能的情况。这可能是NP完全问题。
如果问题涉及序列(如旅行商问题中的城市序列)且难以解决,它可能就是NP完全问题。
如果问题涉及集合(如广播台集合)且难以解决,它可能就是NP完全问题。
如果问题可转换为集合覆盖问题或旅行商问题,那它肯定是NP完全问题。
动态规划
动态规划就是先解决子问题,再逐步解决大问题。
一般用网格法来动态规划,如下面所示: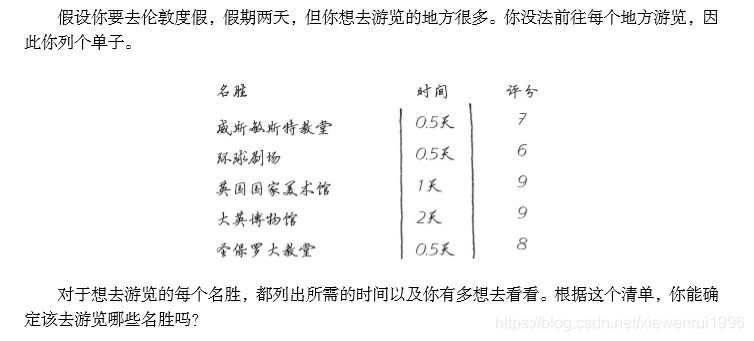
答案如下: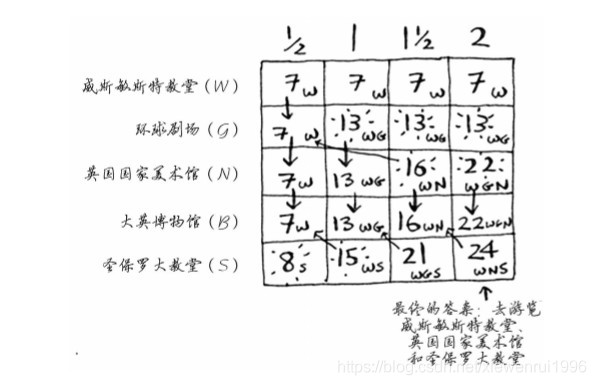
动态规划功能强大,它能够解决子问题并使用这些答案来解决大问题。但仅当 每个子问题都是离散的,即不依赖于其他子问题时,动态规划才管用。
最长公共子串
通过前面的动态规划问题,你得到了哪些启示呢?
动态规划可帮助你在给定约束条件下找到最优解。在背包问题中,你必须在背包容量给定的情况下,偷到价值最高的商品。
在问题可分解为彼此独立且离散的子问题时,就可使用动态规划来解决。要设计出动态规划解决方案可能很难,这正是本节要介绍的。下面是一些通用的小贴士。
每种动态规划解决方案都涉及网格。
单元格中的值通常就是你要优化的值。在前面的背包问题中,单元格的值为商品的价值。
每个单元格都是一个子问题,因此你应考虑如何将问题分成子问题,这有助于你找出网格的坐标轴。
例子:假设你管理着网站dictionary.com。用户在该 网站输入单词时,你需要给出其定义。 但如果用户拼错了,你必须猜测他原本要输入的是什么单词。例如, Alex想查单词fish,但不小心输入了hish。在你的字典中,根本就没有这样的单词,但有几个类似的单词。 在这个例子中,只有两个类似的单词,真是太小儿科了。实际上,类似的单词很可能有数千个。 Alex输入了hish,那他原本要输入的是fish还是vista呢?
答案如下: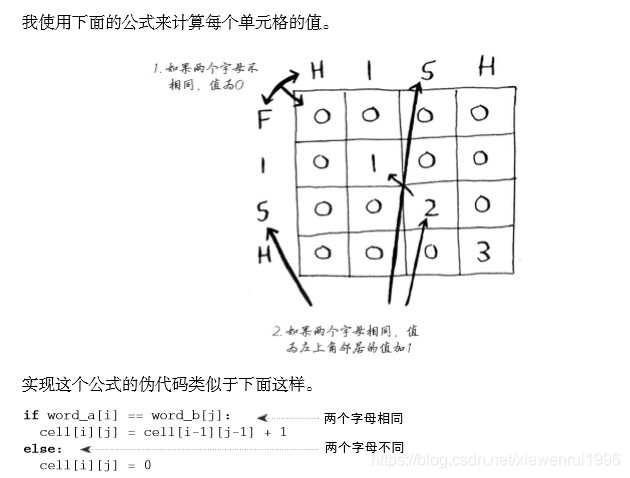
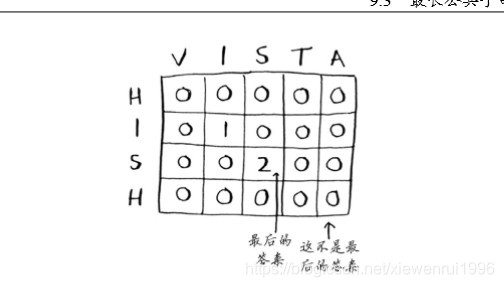
hish和fish的最长公共子串包含三个字母,而hish 和vista的最长公共子串包含两个字母。因此Alex很可能原本要输入的是fish。
最长公共子序列
假设Alex不小心输入了fosh,他原本想输入的是fish还是fort呢?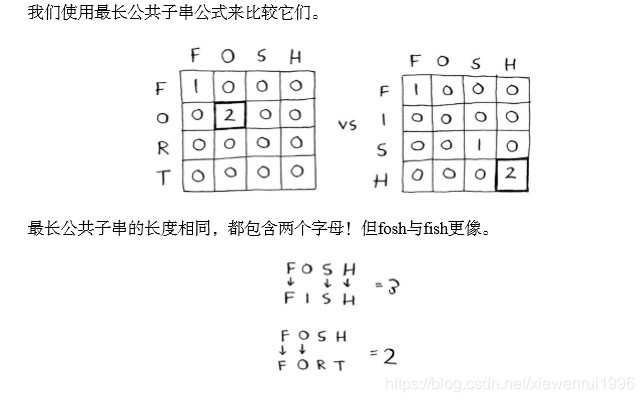
所以我们需要用最长公共子序列来就解决它,如下图: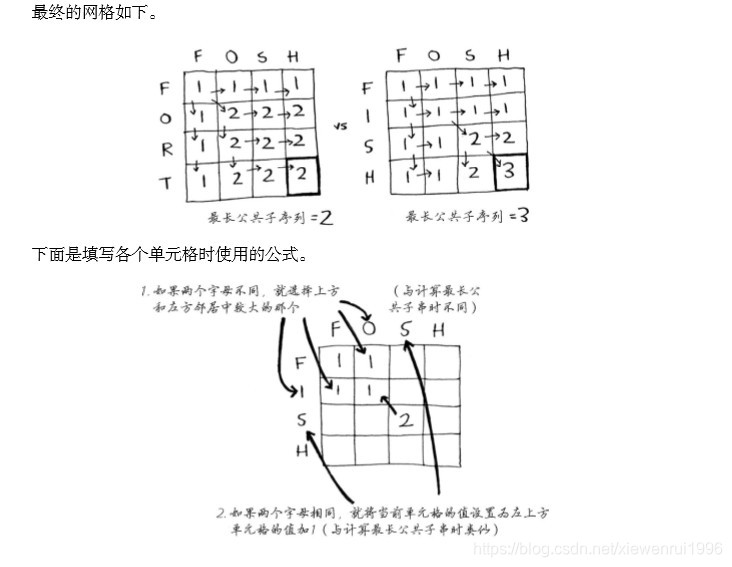
伪代码如下:
if word_a[i] == word_b[j] //两个字母相同
cell[i][j] = cell[i-1][j-1]+1
else:
cell[i][j] = max(cell[i-1][j],cell[i][j-1]
K最近邻算法
即找出跟目标最相近的几个邻居,进行预测或推荐。
创建推荐系统
1、特征抽取
用距离公式来表示相近程度。距离公式很灵活,即便涉及很多个数字,依然可以使用它来计算距离。你可能会问,涉及5个数字时,距离意味着什么呢?这种距离指出了两组数字之间的相似程度。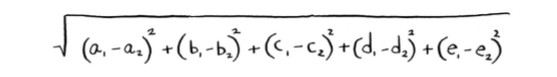
2、回归
- 分类就是编组
- 回归就是预测结果
PS:前面计算两位用户的距离时,使用的都是距离公式。还有更合适的公式吗?在实际工作中,经常使用余弦相似度(cosine similarity)。假设有两位品味类似的用户,但其中一位打分时更保守。他们都很喜欢Manmohan Desai的电影Amar Akbar Anthony,但Paul给了5星,而Rowan只 给4星。如果你使用距离公式,这两位用户可能不是邻居,虽然他们的品味非常接近。 余弦相似度不计算两个矢量的距离,而比较它们的角度,因此更适合处理前面所说的情况。






















 1073
1073

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










