分治法-汉诺塔

问题描述
在汉诺塔游戏中，有三个分别命名为A、B、C得塔座，几个大小各不相同，从小到大一次编号得圆盘，每个原盘中间有一个小孔。最初，所有得圆盘都在A塔座上，其中最大得圆盘在最下面，然后是第二大，以此类推.
代码

package FenZi;

public class HanNuoTa {
	private static int count = 1;
    public static void main(String[] args) {
        moved(4, "第一根柱子", "第二根柱子", "第三根柱子");
    }
    
    /**
     * 
     * @param i  圆盘数量
     * @param a  圆盘初始所在塔座
     * @param b  圆盘将要移动到的塔座
     * @param c     辅助圆盘移动的塔座
     */
    public static void moved(int i,String a,String b,String c){
        if(i == 1){
            disPaly(1, a, b);
        }else{
            //将i-1根圆盘由A移动到C
            moved(i-1, a, c, b);
            //将圆盘i 由A移动到B
            disPaly(i, a, b);
            //将i-1根圆盘由C移动到A
            moved(i-1,c,b,a);
        }
    }
    
    public static void disPaly(int i,String a,String b){
        System.out.println("第"+count+"步：移动第"+i+"个塔从"+a+"到"+b);
        count++;
    }
}

运行结果

第1步：移动第1个塔从第一根柱子到第三根柱子
第2步：移动第2个塔从第一根柱子到第二根柱子
第3步：移动第1个塔从第三根柱子到第二根柱子
第4步：移动第3个塔从第一根柱子到第三根柱子
第5步：移动第1个塔从第二根柱子到第一根柱子
第6步：移动第2个塔从第二根柱子到第三根柱子
第7步：移动第1个塔从第一根柱子到第三根柱子
第8步：移动第4个塔从第一根柱子到第二根柱子
第9步：移动第1个塔从第三根柱子到第二根柱子
第10步：移动第2个塔从第三根柱子到第一根柱子
第11步：移动第1个塔从第二根柱子到第一根柱子
第12步：移动第3个塔从第三根柱子到第二根柱子
第13步：移动第1个塔从第一根柱子到第三根柱子
第14步：移动第2个塔从第一根柱子到第二根柱子
第15步：移动第1个塔从第三根柱子到第二根柱子

算法分析

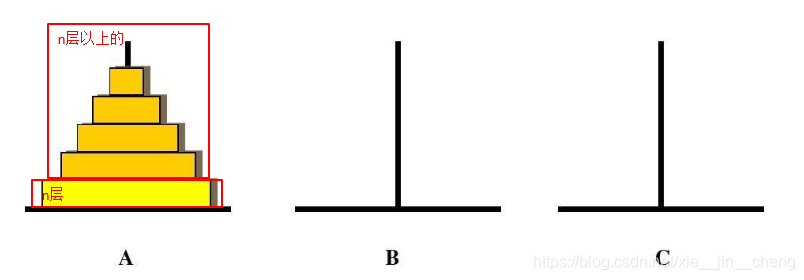
把n盘移到目标柱上
1.先1~n-1盘都移到C柱上，用B做辅助柱
2.把n盘移到B柱上
3.把1~n-1盘移到B柱上，用A做辅助柱
任何数量的盘，都等于先将1~n-1移动到辅助柱上，然后移动n盘。这种递归，直到n=1。