分治算法与汉诺塔问题的详解

本文利用分治算法来解决经典的汉诺塔问题

---

一、分治算法

分治算法是一种很重要的算法。字面上的解释是“分而治之”，就是把一个复杂的问题分成两个或更多的相同的或类似的子问题，再把子问题分成更小的子问题，直到最后子问题可以简单地直接求解,原问题的解即子问题解的合并，这个技巧是很多高效算法的基础，如排序算法（快速排序，归并排序），傅里叶变换（快速傅里叶变换）

分治算法的基本步骤

分治算法在每一层递归上都有三个步骤

1. 分解：将原问题分解为若干个规模较小，相互独立，与原问题形式相同的子问题
2. 解决：将子问题规模较小而容易被解决则直接解，否则递归地解各个子问题
3. 合并：将各个子问题的解合并为原问题的解

二、分治算法处理汉诺塔问题

汉诺塔问题源于印度一个古老的益智玩具，大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着64篇黄金圆盘，大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上，并且规定，再小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘

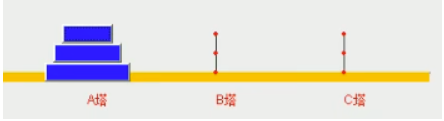
在三个盘的情况下，我们会想办法将最上面的两个盘子移动到B塔上，现将最大的盘子移动到C塔，最后将最上面的两个盘子移动到C塔，完成移动

移动64个盘子我们所遵循的移动思想和3个盘子基本一致

1.汉诺塔思路分析

1. 如果只有一个盘，A->C
2. 如果我们有n>=2的情况，我们总是可以看做是两个盘1.最下面的盘2.上面的盘
   1. 先把最上面的盘A->B
   2. 把最下面的盘A->C
   3. 把B塔的盘移动从B->C

注意，解此类问题时，我们只需按照分治算法的思路，按照将问题分割到最小来解决，在汉诺塔中，无论盘子再多，在我们眼中，只有两个盘子在移动，那就是上面的盘子和下面的盘子，一旦我们将最简单地问题解决，递归会帮助我们解决一切

package org.wql.