内容受限的线性表：串的相关内容

一、串的概念

定义：串是由零个或者多个字符组成的有序序列。一般记为S=“a1a2...an”(n>=0)。当n=0时称为空串（注意与空格串区分）。

串中任意个连续的字符组成的子序列称为该串的子串。

串与线性表的区别：

（1）串的数据对象限定为字符集；（英文字符——ASCII，中英文——Unicode）

（2）串的基本操作通常以子串为操作对象，而线性表以单个元素作为操作对象。

二、串的基本操作

StrAssign (&T)：赋值操作

StrCopy(&T,S)：复制操作

StrEmpty(S)：判空操作，可以看长度。

StrLength (S)：求串长，return length。

Concat(&T,S1,S2)：串联接，考虑存储空间扩展问题。 

ClearString (&S)：清空操作，length=0。

DestroyString(&S)：销毁串，释放空间。

Index(S,T)：定位操作

SubString(&Sub,S,pos,len)：求子串

StrCompare (S,T)：比较操作

三、串的存储结构

1、定长顺序表示

#define MAXLEN 255   //预定义最大串长255
typedef struct{
    char ch[MAXLEN];   //每个分量存储一个字符
    int length;   //串的实际长度
}SString;

这里所用的顺序存储的字符串从下标为1的数组分量开始存储，下标为0的分量闲置不用。（本文采用的存储方式）

有的教程采用ch[0]充当length，缺点是只可以表示0-255的长度；还有在串值后面加一个不计入串长的结束标记字符‘\0’，此时的串长为隐含值，缺点是每次需遍历求串长。

2、堆分配存储表示

typedef struct{
    char *ch;   //按串长分配存储区，ch指向串的基地址
    int length;   //串的长度
}HString;

HString S;
S.ch=(char *)malloc(MAXLEN*sizeof(char));
S.length=0;

在C语言中，存在一个称为“堆”的自由存储区，并用malloc()和free()函数来完成动态存储管理。

3、块链存储表示

typedef struct StringNode{
    char ch;   //每个结点存1个字符
    struct StringNode *next;
}StringNode,*String;

typedef struct StringNode{
    char ch[4];   //每个结点存多个字符
    struct StringNode *next;
}StringNode,*String;

由于串的特殊性，在具体实现时，每个结点既可以存放一个字符（存储密度低，每个字符1B，每个指针4B），也可以存放多个字符（存储密度提高，最后一个结点占不满时常用“#”或“\0”补上）。每个结点称为块，整个链表称为块链结构。

4、基本操作的实现（部分）

①赋值操作

//赋值操作
void StrAssign(SString &str)
{
	char cc;
	int i=0;
	scanf("%c",&cc);
	while(cc!='#'&&i<MAXLEN)
	{
		i=i+1;
		str.ch[i]=cc;
		scanf("%c",&cc);
	}
	str.ch[i+1]='\0';  //字符串结束标记
	str.length=i;  //串长为i
}

②求子串

//求子串
bool SubString(SString &s1,SString &s,int pos,int len)
{
	if(pos+len-1>s.length)//子串范围越界
		return false;
	for(int i=pos;i<pos+len;i++)
		s1.ch[i-pos+1]=s.ch[i];
	s1.length=len;
	return true;
}

③比较操作

//比较操作
int StrCompare(SString S,SString T)
{
	//若S>T，则返回值>0；若S=T，则返回值=0，若S<T,则返回值<0
	for(int i=1;i<=S.length&&i<T.length;i++)
	{
		if(S.ch[i]!=T.ch[i])
			return S.ch[i]-T.ch[i];
	}
	//扫描过的所有字符都相同，则长度长的串更大
	return S.length-T.length;
}

④定位操作

//定位操作
int Index(SString S,SString T)
{
	int i=1,n=S.length,m=T.length;
	SString sub;//用于暂存子串
	while(i<=n-m+1)
	{
		if(SubString(sub,S,i,m))
		{
			if(StrCompare(sub,T)!=0)
				++i;
			else
				return i;//返回子串在主串的位置
		}
	}
	return 0;//S中不存在与T相等的子串
}

四、串的模式匹配

1、BF算法（又称古典的、经典的、朴素的、穷举的）

算法思想：

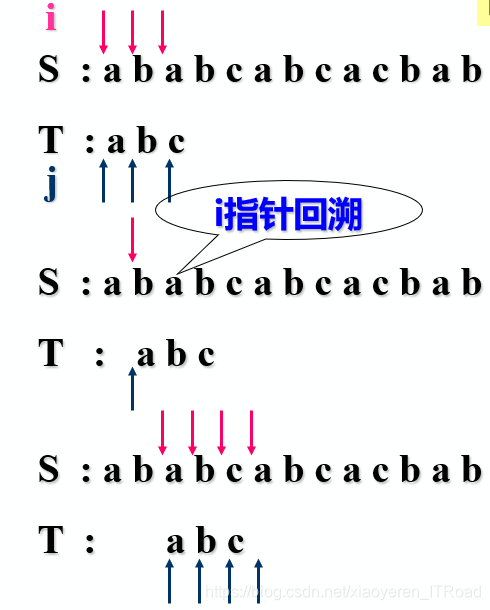
（1）将主串的第pos个字符和模式的第一个字符比较，若相等，继续逐个比较后续字符；若不等，从主串的下一字符起，重新与模式的第一个字符比较；

（2）直到主串的一个连续子串字符序列与模式相等 。返回值为S中与T匹配的子序列第一个字符的序号，即匹配成功。否则，匹配失败，返回值 0。

算法时间复杂度：O(n*m)

//简单模式匹配算法(BF)
int BFIndex(SString S,SString T)
{
	int i=1,j=1;//i,j分别指向主串和模式串
	while(i<=S.length&&j<=T.length)
	{
		if(S.ch[i]==T.ch[j])
		{
			i++;//继续比较后续字符
			j++;
		}
		else
		{
			i++;//检查下一子串
			j=1;
		}
	}
	if(j>T.length)
		return i-T.length;
	else
		return 0;
}

2、KMP算法（特点：速度快）

算法思想：

此算法可以在O(n+m)的时间数量级上完成串的模式匹配操作。其改进在于：每当一趟匹配过程中出现字符比较不等时，不需回溯i指针，而是利用已经得到的“部分匹配”的结果将模式向右“滑动”尽可能远的一端距离后，继续进行比较。

模式串的next函数的定义：

    next[i][j]=k:

    ①当j=1(t1与si比较不等时，下一步进行t1与si+1的比较)时Max{k|1<k<j且有＂t1t2. . .tk-1"="tj-k+1tj-k+2. . .tj-1"}

    ②k=1(不存在相同子串，下一步进行t1与si的比较）

KMP算法描述：

int Index_KMP(Sstring S, Sstring T,int pos)
{
   //利用模式串T的next函数求T在主串S中第pos个字符之后的位置
  //其中，T非空，1<=pos<=S.length
 
   i=pos;j=1;
   while(i<=S.length&&j<=T.length)   //两个串均未比较到串尾
   {
      if(j==0||S.ch[i]==T.ch[j]){++i; ++j;}   //继续比较后继字符
      else j=next[j];   //模式串向右移动
   }
   if(j>T.legnth)return i-T.length;   //匹配成功
   else return 0;   //匹配失败
}

计算next函数值的算法描述：

void get_next(Sstring T,int next[])
{
   //求模式串T的next函数值并存入数组next
   i=1;next[1]=0;j=0;
   while(i<T.length)
   {
      if(j==0||T.ch[i]==T.ch[j]){++i;++j;next[i]=j;}
      else j=next[i][j];
   }
}

计算next函数修正值的算法描述：

void get_nextval(Sstring T,int nextval[])
{
   //求模式串T的next函数修正值并存入数组nextval 
   i=1;nextval[1]=0;j=0;
   while(i<T.length)
   {
      if(j==0||T.ch[i]==T.ch[j])
      {
         ++i;++j;
         if(T.ch[i]!=T.ch[j])nextval[i]=j;
         else nextval[i]=nextval[j];
      }
      else j=nextval[j];
   }
}