概率分布、概率分布函数

离散型随机变量

概率函数

• 概率函数是用函数的形式表示概率
• $$P_i=P(X=a_i)(i=1,2,3,4,5,6)$$
  在这个函数里，自变量 X 是随机变量的取值，因变量 $P_i$是取值的概率。它就代表了每个取值的概率，所以顺理成章的它就叫做了X的概率函数。从公式上来看，概率函数一次只能表示一个取值的概率。比如P（X=1）=1/6,这代表用概率函数的形式来表示，当随机变量取值为1的概率为1/6，一次只能代表一个随机变量的取值。

概率分布

X	$x_1$ , $x_2$ , $x_3$ , $x_4$ …
$P_i$	$p_1$ , $p_2$ , $p_3$, $p_4$ …

这个列表，上面是值，下面是这个取值相应取到的概率。概率分布要把所有可能出现的情况全部都列出来。

概率分布函数

F(x)就代表概率分布函数

• 概率分布函数是概率函数取值的累加结果，又叫累积概率函数。

连续型随机变量

概率密度函数及概率分布函数

$$P(a\le X\le b)=F(b)-F(a)={\int }_a^{b}f(x)dx$$

• 概率密度函数用数学公式表示就是一个定积分的函数，面积即为概率。
  
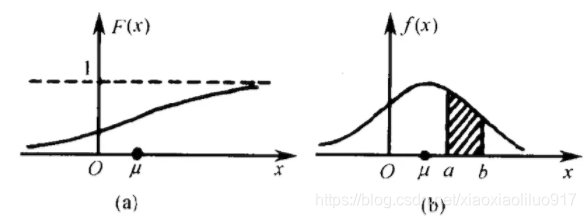
• 左边F(x)是连续型随机变量分布函数画出的图形，右边f(x)是连续型随机变量的概率密度函数画出的图像，它们之间的关系就是，概率密度函数是分布函数的导函数。
• 如果用右图中的面积来表示概率，利用图形就能很清楚的看出，哪些取值的概率更大！