二叉搜索树-利用循环删除二叉搜索树算法

感谢:爱你是长久之计~博主提供思想(私下,技术交流)

利用循环删除二叉搜索树算法-算法流程图

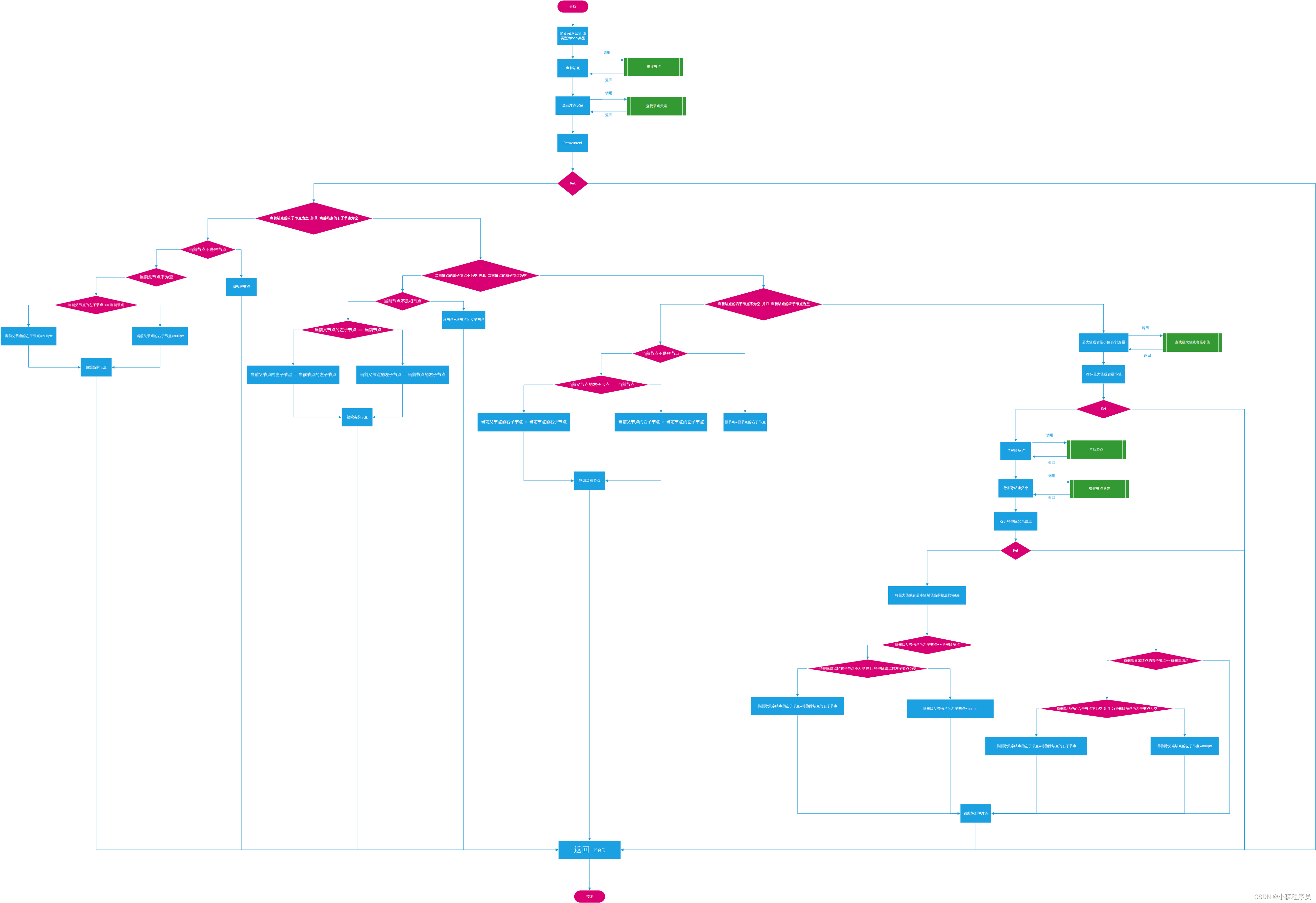
利用循环删除二叉搜索树算法-算法实现

//通过循环查找节点
Tree::Tree_Node* Loop_FindTreeNode(Tree::Tree_Node*& root, const Tree::Tree_value &value) {

	auto  currentNode = root;
	while (currentNode&& currentNode->value != value){
		if ((currentNode->value> value)){
			currentNode = currentNode->LeftChild;
		}		
		else {
			currentNode = currentNode->RightChild;
		}

	}

	return currentNode;

}

Tree::Tree_Node* Loop_FindTreeParentNode(Tree::Tree_Node*& node, const Tree::Tree_value& value) {

	Tree::Tree_Node* Parent = nullptr;
	auto  currentNode = node;
	while (currentNode && currentNode->value != value) {
		Parent = currentNode;
		if ((currentNode->value > value )) {
			currentNode = currentNode->LeftChild;
		}
		else {
			currentNode = currentNode->RightChild;
		}

	}
	//如果currentNode != nullptr 返回Parent 父亲节点 否则返回 nullptr
	return currentNode != nullptr ? Parent : nullptr;

}

int *Loop_FindTreeMaxOrMinValue(Tree::Tree_Node*& node) {

	int* MaxOrMinValue = nullptr;
	auto  currentNode = node;
	if (currentNode){


		if (currentNode->LeftChild) {

			currentNode = currentNode->LeftChild;

			while (currentNode->RightChild) {

				currentNode = currentNode->RightChild;

			}

			MaxOrMinValue = &currentNode->value;

		}
		else if (currentNode->RightChild){

			currentNode = currentNode->RightChild;

			while (currentNode->LeftChild) {

				currentNode = currentNode->LeftChild;

			}

			MaxOrMinValue = &currentNode->value;

		}
	}
	//如果MaxOrMinValue != nullptr 返回MaxOrMinValue  否则返回 nullptr
	return MaxOrMinValue != nullptr ? MaxOrMinValue : nullptr;

}


 inline bool Is_TreeNodeSame( Tree::Tree_Node*& treeNodeOnce,  Tree::Tree_Node*& treeNodeTwo) {
	return (treeNodeOnce == treeNodeTwo);
}

 void  unlinkTreeNodeLeftChild(Tree::Tree_Node*& TargetNode, Tree::Tree_Node* SourceNode = nullptr) {
	

	 TargetNode ? TargetNode->LeftChild = SourceNode : TargetNode;
 }
 void  unlinkTreeNodeRightChild(Tree::Tree_Node*& TargetNode, Tree::Tree_Node* SourceNode = nullptr) {

	 TargetNode ? TargetNode->RightChild = SourceNode : TargetNode;
 }

 void Destroy_treeNode(Tree::Tree_Node*& TreeNode, nullptr_t where=nullptr) {
	 delete TreeNode;
	 TreeNode = where;
 }


//循环方式删除二叉搜索树结点
 bool Loop_DeleteTreeNode(Tree::Tree_Node*& root, const Tree::Tree_value& value) {

	 bool ret = false;


	 //当前 节点
	 Tree::Tree_Node* currentNode = Loop_FindTreeNode(root, value);
	 //当前结点父节点
	 Tree::Tree_Node* currentParentNode = Loop_FindTreeParentNode(root, value);

	 ret = currentNode;
	 if (ret) {
		 //当前节点的左子节点有节点 并且 当前节点的右子节点有节点 的情况
		 if (!currentNode->LeftChild && !currentNode->RightChild) {

			 //当前节点不是根节点
			 if (!Is_TreeNodeSame(currentNode, root)) {
				 //当前父节点不为空
				 if (currentParentNode) {
					 //当前父节点的左子节点 == 当前节点
					 if (Is_TreeNodeSame(currentParentNode->LeftChild, currentNode)) {
						 //调用断开树的节点的左子节点
						 unlinkTreeNodeLeftChild(currentParentNode);
					 }
					 //当前父节点的右子节点 == 当前节点
					 else {
						 //调用断开树的节点的右子节点
						 unlinkTreeNodeRightChild(currentParentNode);
					 }
				 }
			 }
			 else {
				 //销毁树的节点
				 Destroy_treeNode(currentNode);
				 root = currentNode;
			 }
			
			 //销毁树的节点
			 Destroy_treeNode(currentNode);
		 }//当前节点的左子节点没有节点 并且 当前节点的右子节点没有节点 的情况	
		 else if (currentNode->LeftChild && !currentNode->RightChild) {
			 if (!Is_TreeNodeSame(currentNode, root)) {
				 //当前父节点不为空
				 if (currentParentNode) {
					 //当前父节点的左子节点 == 当前节点
					 if (Is_TreeNodeSame(currentParentNode->LeftChild, currentNode)) {
						 //调用断开树的节点的左子节点
						 unlinkTreeNodeLeftChild(currentParentNode, currentNode->LeftChild);
					 }
					 else {
						 //调用断开树的节点的右子节点
						 unlinkTreeNodeRightChild(currentParentNode, currentNode->LeftChild);
					 }
				 }
						
			 }
			 else {
				 //根节点向左子节点 方向走
				 root = root->LeftChild;
			 }

			 //销毁树的节点
			 Destroy_treeNode(currentNode);
		 }
		 //当前节点的左子节点没有节点 并且 当前节点的右子节点有节点 的情况
		 else if (!currentNode->LeftChild && currentNode->RightChild) {
			 if (!Is_TreeNodeSame(currentNode, root)) {

				 if (currentParentNode) {

					 //当前父节点的右子节点 == 当前节点
					 if (Is_TreeNodeSame(currentParentNode->LeftChild, currentNode)) {
						 //调用断开树的节点的左子节点
						 unlinkTreeNodeLeftChild(currentParentNode, currentNode->RightChild);
					 }
					 else {
						 //调用断开树的节点的右子节点
						 unlinkTreeNodeRightChild(currentParentNode, currentNode->RightChild);
					 }	
				 }				
			 }
			 else {
				 //根节点向右子节点 方向走
				 root = root->RightChild;
			 }
			 //销毁树的节点
			 Destroy_treeNode(currentNode);
		 }
		 //当前节点的左子节点有节点 并且 当前节点的右子节点有节点 的情况
		 else {
			 //自动获取最大或者最小值
			const int* MaxOrMinValue = Loop_FindTreeMaxOrMinValue(currentNode);

			 ret = MaxOrMinValue;
			 if (ret) {

				 //缓存需要待删除结点
				 auto CacheNode = Loop_FindTreeNode(root, *MaxOrMinValue);
				 //缓存需要删除的父节点
				 auto CacheNodeParent = Loop_FindTreeParentNode(root, *MaxOrMinValue);
				 ret = CacheNodeParent;
				 if (ret){
					 //当前结点的数据改为最大或者最小值
					 currentNode->value = *MaxOrMinValue;
					 
					 //缓存需要待删除父节点的左子节点==CacheNode
					 if (CacheNodeParent->LeftChild == CacheNode) {
						 
						 //缓存节点的左子节点有节点 并且 缓存节点的右子节点没有节点 的情况
						 if (CacheNode->RightChild && !CacheNode->LeftChild) {
							 //调用断开树的节点的左子节点 
							 unlinkTreeNodeLeftChild(CacheNodeParent, CacheNode->RightChild);
						 }
						 else {
							 //调用断开树的节点的左子节点
							 unlinkTreeNodeLeftChild(CacheNodeParent);
						 }
					 } //缓存待删除结点
					 else  if (CacheNodeParent->RightChild == CacheNode) {
						 //缓存待删除结点的左子节点有节点 并且 缓存待删除结点的右子节点没有节点 的情况
						 if (CacheNode->LeftChild && !CacheNode->RightChild) {
							 unlinkTreeNodeRightChild(CacheNodeParent, CacheNode->LeftChild);
						 }
						 else {
							 //调用断开树的节点的右子节点
							 unlinkTreeNodeRightChild(CacheNodeParent);
						 }
					 }

					 Destroy_treeNode(CacheNode);
				 }
			 }
		 }
	 }

	 return ret;
 }


 void TreeErase(Tree& tree, const Tree::Tree_value& value) {

	 Loop_DeleteTreeNode(tree.Root, value);
	 tree.size -= 1;

 }