二叉搜索树-遍历算法

递归遍历

前序遍历

一句话 :先根 再左 后右

先遍历根节点 再遍历左子树, 再遍历右子树

遍历算法分析图

1. 遍历根节点 和 遍历左子树

2. 遍历右子树

2. 遍历右子树 ,并且 遍历 完毕 返回到 根节点的右子树

中序遍历

一句话 :先左 再根 后右

先遍历左子树 再遍历根节点 , 再遍历右子树

遍历算法分析图:

== 遍历左子树 和 遍历根节点 ==

后序遍历

一句话 :先左 再右 后跟

递归遍历算法分析图:

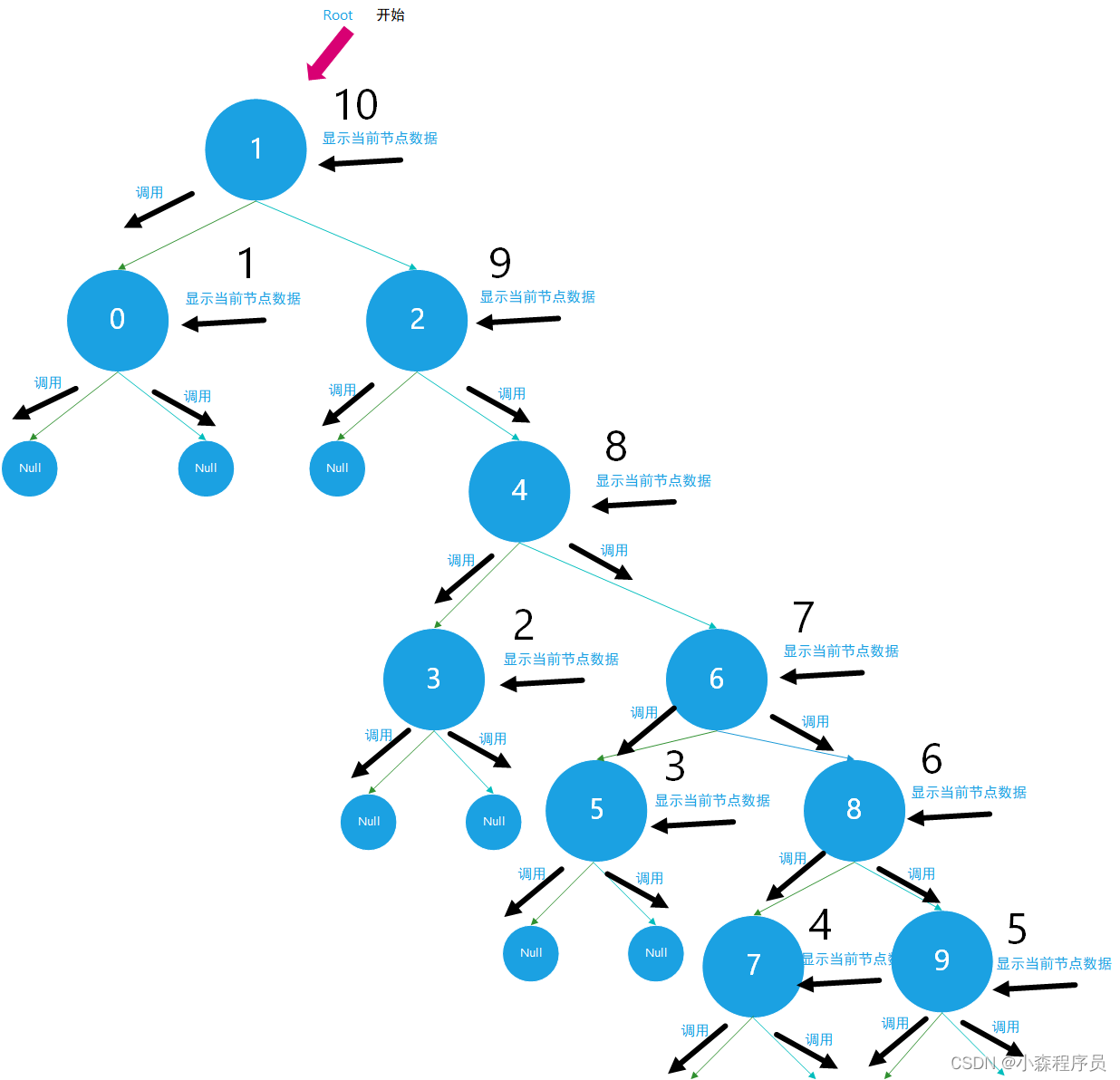
代码?想必各位已经里解了吧 ,代码也就是那几行 多思考多做,和多画, 在非递归后序遍历 更加抽象化并且扭曲化 可能是最难的
但是有写的好后序遍历,没有没一点问题的都可以直接拿去用 .除非你强,不然 用别人的也是不错的选择 …

非递归遍历

中序遍历

非递归中序遍历理解图

非递归遍历思想:
当前树节点指向根节点
若栈非空 或者 当前树节点也非空
1 循环遍历左子树并且将根节点和左子树
2 获取左子树
3 输出左子树 以及根节点 以及右子树 以上 非递归中序遍历理解图 为例
4. 当前树节点指向右子节点
4.再遍历根节点
5 再遍历右子树
6 直到栈为空

非递归遍历算法实现

//非递归中序遍历
static void InOrderNonRecursiveTraversal(TreeNode*& Root) {

	SeqStack Stack;
	initStack(Stack);
	
	auto CurrentNode = Root;
	while (!emptyStack(Stack) || CurrentNode) {

		while (CurrentNode) {
			push_Stack(Stack, CurrentNode);
			CurrentNode = CurrentNode->LeftChild;
		}

		CurrentNode = TopStack(Stack);
		cout << " " << CurrentNode->value << "-> ";
		pop_Stack(Stack);
		CurrentNode = CurrentNode->RightChild;
	}
	
	destroyStack(Stack);
}