本文介绍了概率图模型，重点讨论了背景和概率模型的基础，包括加法法则、乘法法则、链式法则和贝叶斯法则。探讨了高维随机变量的计算困境，并提出两种简化方法：独立性和马尔可夫性质。文章还提到了条件独立性作为概率图模型的核心概念，并区分了有向图（贝叶斯网络）、无向图（马尔可夫网络）以及高斯图。最后，简要提及了推断和学习在概率图模型中的应用。
概率图模型
感谢B站up主@shuhuai008！
本文是学习他发布在b站上的概率图模型视频的一些笔记。
地址：https://www.bilibili.com/video/av33545406
P1 背景介绍
可以从两个角度来看概率图模型，即一个是概率，一个是图。
要预测其实概率就足够了，这个图，其实是一个工具。我们在数据结构中也有图，但都是比较抽象的；这里的图，其实是把原来数据结构中的图，赋予了概率，把概率嵌进去，使得整个模型更加清晰，也可以进一步构建更高级的模型。
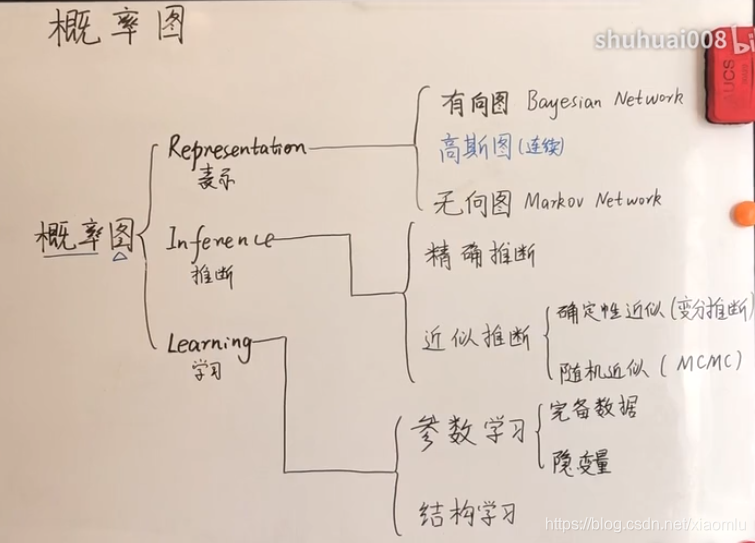
我们先来看看概率这一块。
概率在建模过程中，其实是对现实问题的一个抽象。我们关注的问题，我们的数据往往是多维的，因此我们在用随机变量表示问题的时候，就会假设这是一个高维的随机变量。
也就是说，我们概率模型关注的对象其实就是高维的随机变量，或者说是它的概率分布。我们对这个高维随机变量可以做很多事情，比如求边缘概率，条件概率。
在进行概率计算的过程中，有两个很重要基本的法则——加法法则和乘法法则。
- 加法法则 Sum Rule (求和就其实是求积分)
P ( x 1 ) = P ( x 1 , x 2 ) d x 2 P(x_1) =P(x_1,x_2)dx_2 P(x1)=P(x1,x2)dx2 - 乘法法则 Product Rule
P ( x 1 , x 2 ) = p ( x 1 ) p ( x 2 ∣ x 1 ) = p ( x 2 ) p ( x 1 ∣ x 2 ) P(x_1,x_2)=p(x_1)p(x_2|x_1)=p(x_2)p(x_1|x_2) P(x1,x2)=p(x1)p(x2∣x1)=p(x2)p(x1∣x2)
引申有链式法则，其实就是对上述两个法则的泛化。
- 链式法则 Chain Rule
P ( x 1 , x 2 , . . . , x p ) = ∏ i = 1 p P ( x i ∣ x 1 , x 2 , . . . , x i − 1 ) P(x_1,x_2,...,x_p)=\prod_{i=1}^p{P(x_i|x_1,x_2,...,x_{i-1})} P(x1
最低0.47元/天 解锁文章
扫一扫
674
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
