白板推导系列 - SVM支持向量机

支持向量机

视频地址

https://www.bilibili.com/video/av28186618
非常感谢这位up！真的好感谢！讲的很清楚！膝盖都跪碎了！
感谢b站up主@shuhuai008

P1: 硬间隔SVM - 模型定义(最大间隔分类器)

SVM有三宝：间隔，对偶，核技巧
SVM的三种类别：
1）Hard-Margin SVM 硬间隔SVM
2）Soft-Margin SVM 软间隔SVM
3）Kernal SVM

不同类别会采用不同的算法，最基础的是硬间隔SVM，也是这一讲的主要内容。
先从几何角度来看。SVM最初的提出是为了解决二分类问题。分类任务就是找到一条线，把平面上两个类别的样本正确地分开。如果把这条分割的线定义为超平面，超平面为$w^{T}x+b$，模型写作$f(w)=sign(w^{T}x+b)$。这个sign表示如果括号里的数值大于0，则属于1，小于0时，属于-1。
此时，SVM是一个纯粹的判别模型，和概率是没有关系的。

但是有无限条线可以正确地把两组点分开，SVM的特别之处在于，可以从几何意义上找到一条最好的线。因为，我们不仅仅关注训练误差，更加关注的是期望损失/测试误差。如果一条直线和一个点非常近，那么它的鲁棒性就可能不太好，可能会受到噪声的影响；所以我们要找的是最中间的一个超平面，让它离所有样本点的距离都足够的大。

硬间隔SVM又叫作，最大间隔分类器。
用数学公式表示，即：

有N个样本点：$(x_i,y_i),x_i\in R^p,y_i\in -1,1$
margin是一个定义间隔的函数，和w,b相关。
(注：最优化问题一般求解最小，因此过程中有些求最大转化为求最小的过程)
最后可以转化为一个凸优化的问题。

如果维度不高，其实就是一个QP问题；如果比较复杂，才会引入对偶、kernal等用于求解。在后面几P会解释。

本次主要要注意把几何意义化作数学表达。

P2: 硬间隔SVM - 模型求解(对偶问题之引出)

（本节中会忽略一些严格的定理证明）
首先，把上P讲到的凸优化问题（对w，b带有约束）——目标函数和优化条件，借助拉格朗日函数把问题化成无约束的（对w与b没有约束，只对${\lambda }_i$有约束条件）问题。
注意到，拉格朗日乘子的一些限制，${\lambda }_i>=0$，后面相乘的式子要小于等于0。

然后通过一个比较简化的证明，可以证明我们的通过拉格朗日的转化后得到的式子的解和原来的式子的解是等价的。
由此，我们也求解出：
$mi{n}_{w,b}ma{x}_{\lambda }L(w,b,\lambda )=mi{n}_{w,b}\frac{1}{2}{w}^{T}w$

其实，仔细去理解一下，你会发现，拉格朗日转化后的式子，虽然没有明确写出一些约束条件，但是在求解过程中，其实还是会自然处理好这部分问题的。

以上的两个式子是原问题，然后我们利用对偶关系，进一步更新转化这个要求解的问题。

首先，我们要理解一个式子（不严格证明），即弱对偶关系：
$min\max (f)>=max\min (f)$
用up的宁为鸡头，不为凤尾理论，我们可以这样理解为——凤里的凤尾>=鸡里的鸡头。
这样的一个关系，叫做弱对偶关系。

但我们最想要的其实是一个强对偶关系，也就是：
$min\max (f)=max\min (f)$

而我们的优化问题，要优化的函数：它的目标函数是一个凸二次的，它的约束也是线性的；所以在理论上它是满足强对偶条件的（证明略过），因此我们就直接利用下这个强对偶条件。

得到：

注意到，$max\max (L(w,b,\lambda ))$里面那层的min的式子，对w和b是没有约束的，所以我们就直接通过求偏导，零其为0。
过程中也有一些运算：

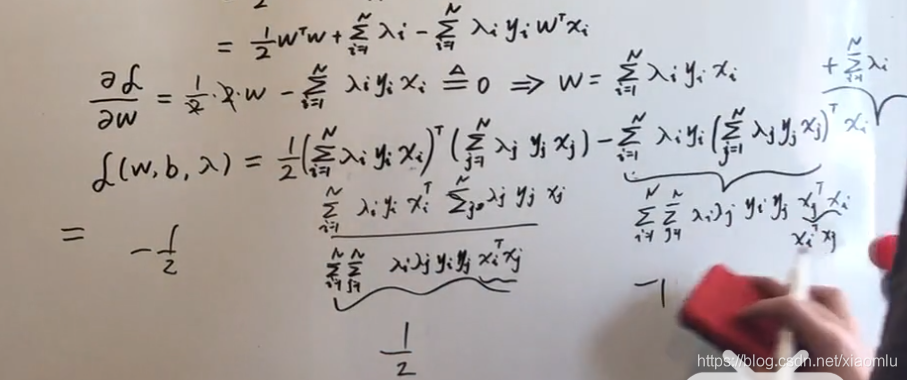
得到：

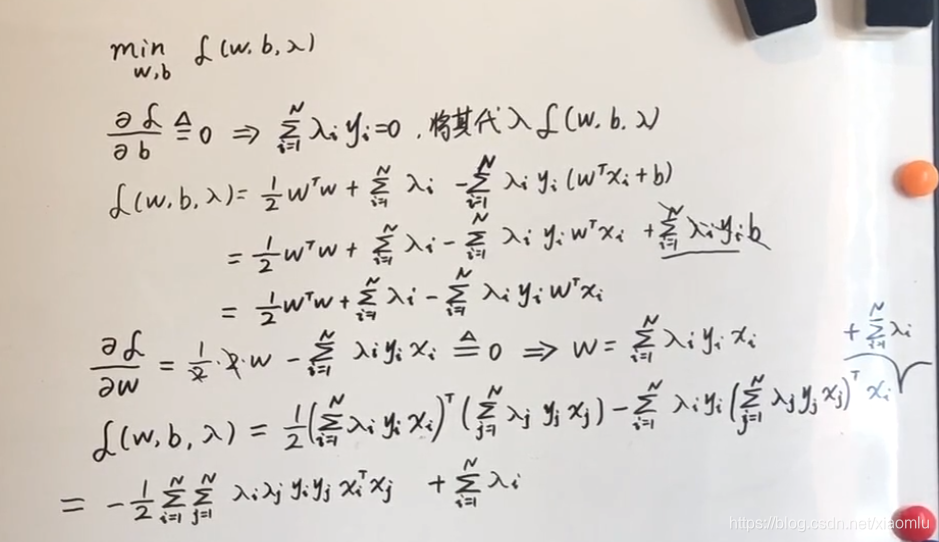
此时已经得到，令里面那层达到min的w值为$w={\sum }_{i=1}^N{\lambda }_i{y}_i{x}_i$。

里面那层的数值相当于，已经就算出，那么现在就继续算外面那一层的。

这一节就到这里。

P3：硬间隔SVM - 模型求解（对偶问题之KKT条件）

介绍KKT条件，以解决P2最后连列式的求解。
首先介绍KKT条件，这是对拉格朗日公式的一些条件。
这里先写出来：

那么什么是KKT条件呢？
原问题、对偶问题具有强对偶关系 充要条件是 满足KKT条件。因为我们的问题是满足强对偶关系的（没有证明），所以我们可以用KKT条件求解这个问题。