Hybrid A*算法研究

最新推荐文章于 2025-08-19 14:20:28 发布

原创最新推荐文章于 2025-08-19 14:20:28 发布 · 967 阅读

18 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #自动驾驶 #机器人

机器人&自动驾驶专栏收录该内容

4 篇文章

订阅专栏

主要参考资料：
论文：Practical Search Techniques in Path Planning for Autonomous Driving
代码：https://github.com/karlkurzer/path_planner
Hybrid A* Path Planner for the KTH Research Concept Vehicle
作者：karlkurzer
其他:
混合A算法研究_robinvista的博客-优快云博客_混合a星
混合A算法—Hybrid A Star_一米八八的超儿的博客-优快云博客_混合a*

1. 背景

1.1 考虑机器人动力学约束下的路径寻找介绍

Kinodynamic : Kinematic + Dynamic（运动学+动力学）

受到高阶微分约束
力的约束(加速度)

运动学规划问题是在同时受到运动学约束(如避障)和动力学约束(如速度、加速度和力的模量界限)的情况下综合机器人运动。动力学解是从时间到广义力或加速度的映射。——《动力学运动规划》，Bruce Donald, Patrick Xavier, John Canny, John Reif

为啥要在路径规划的时候考虑动力学约束？
通过路径搜索算法(基于图搜索的路径搜索算法（如A*），也有基于采样的路径搜索算法（如RRT、RRT*）)，我们能够得到一条可通行的路径，然而，对于这条路径中的路标点（Waypoint）之间的路径往往是不符合机器人（无人机\无人车）动力学模型的。
因此，对于每一个路标点（Waypoint）之间的连接路径，我们需要进行进一步的优化，从而得到一条符合机器人（无人机\无人车）动力学约束的可通行的运动学连接（feasible motion connections）。

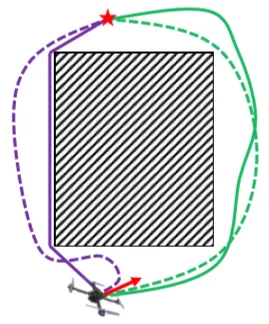
在这里插入图片描述
如上图中实线为前端路径搜索得到的可通行路径，而虚线为后端轨迹优化得到的符合动力学模型的可通行路径。经典的运动规划算法框架，往往由前端路径搜索与后端轨迹优化组成，在得到满足运动学的可通行的运动连接后，才能够将这条优化后的轨迹指令下达至控制器执行。

在这里插入图片描述
总结来说，由于系统的微分约束，状态对之间的直线连接通常不是有效的轨迹，而

路径规划是一个coarse-to-fine process(由粗到精）
轨迹优化只能在局部进行优化(局部优化不一定能满足动力学约束)
不可行路径对非完整系统没有意义

1.2 什么情况下要考虑动力学约束的运动规划（graph search不能满足需求）

1.2.1 状态栅格规划(State Lattice Planning)

假设把机器人作为质点的模型已经不能适用，需要对建立的图的节点连接，采用能满足机器人运动的约束曲线进行连接。使得，生成一个机器人能真正执行运动的边路径。这里，有两种方法：

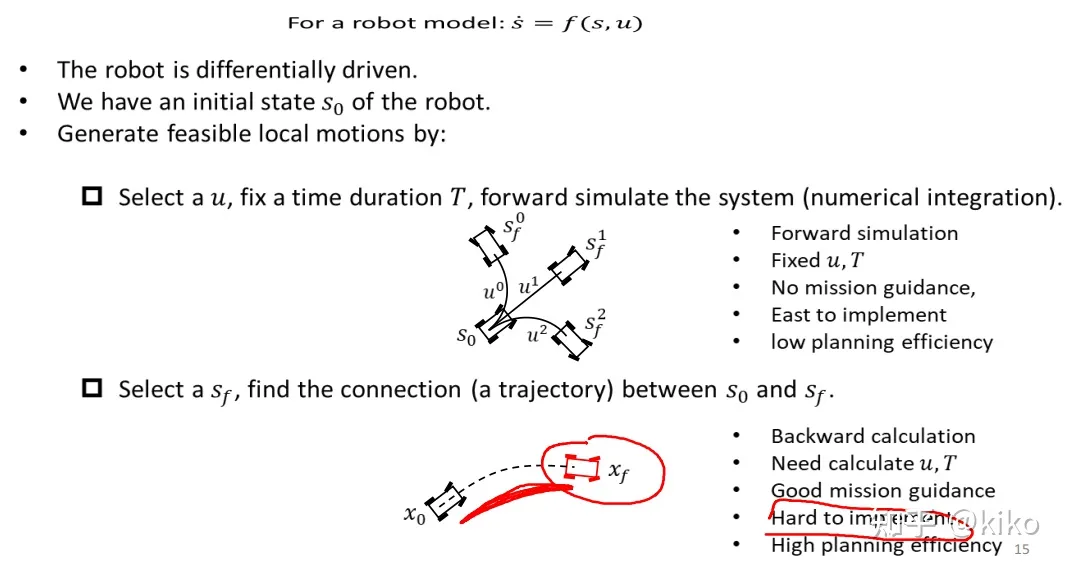
Forward direction(正向方法)：把机器人的控制空间进行离散(确定控制量u)，驱动机器人往前运动，得到一个个的feasible motion connections（N连接图其实就是这个方法）
Reverse direction(逆向方法)：把机器人的状态空间进行离散(确定状态量s)，连接状态，形成一条feasible motion connections（PRM就是这个方法）

在这里插入图片描述

1.2.2 对比分析

状态空间采样与控制空间采样对比：

在控制空间进行采样，如果没有加入启发函数，会没有目的性。在状态空间进行采样，有了目的性，能最大限度的保证有最多的局部轨迹可以使用
如果只是去离散控制空间，自由度比较少(把u,T固定)，在一段时间内，feasible local motion会有很强的同质化，会很大的受到初始状态的影响
所以，在状态空间进行离散，更优，但是，一个难点在于，很难通过起始状态和中间状态去解算中间的控制量(hard to implement)，这里，需要用到Boundary Value Problem(边界值问题)

1.2.3 Boundary Value Problem(BVP)

BVP是状态采样点阵规划的基础
没有通用的解决方案。只能逐个设计
经常进行复杂的数值优化：需要求解状态空间采样的问题

系统描述
根据边界条件求解方程，给定5阶轨迹多项式：
给定5阶的轨迹多项式：

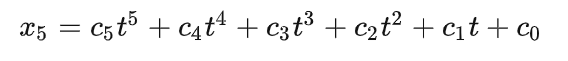
边界约束：

则解为：

最小化的目标值为三个轴的jerk(position的三次导数)平方和【无人机系统可以简化成三个单轴的系统】
模型：

对状态求导，得到的变量也就是 (vk,ak,jk)
状态求解
引入庞德里亚金的极小值原理：

定义问题的协态(costate)和哈密尔顿函数：
λ=(λ1,λ2,λ3)

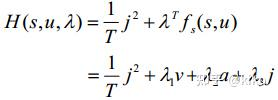
在这里插入图片描述

如果指定 s(T)=s(f) ，，则目标状态约束为硬约束， h=0 ，如果最终没到达，则 h=∞ ，所以这里的 λ(T) 不可导。
协态(costate)和哈密尔顿函数为：
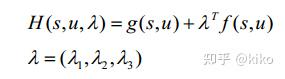
要求出满足目标函数最小输入和状态：

小车的模型
几何表示（碰撞检测中使用）

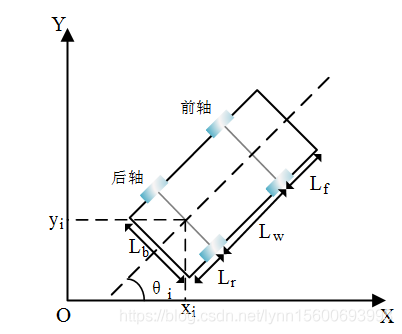
以车辆后轴中心位置（x,y，theta）代表车辆当前位置，对于车辆的某一位姿，相当于一个矩形落在另一个矩形中首先根据状态变量算出车辆的四个顶点坐标：

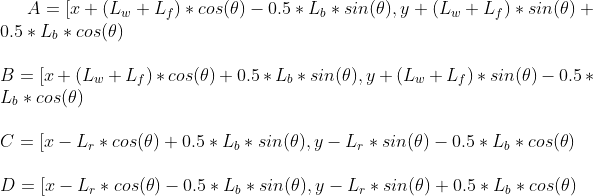
Lw为前后轴距，Lf为车辆前悬距离，Lr为车辆后悬距离，Lb为车宽。根据车辆后轴中心坐标与车辆航向角即可以计算出车辆的四个顶点，目标泊车区域可以通过四条直线方程来表示，想要泊车目的达到，只需要建立四个点在泊车区域内的点约束方程组即可。
运动学模型（规划与控制中使用）
小车模型比无人机少了一个维度(侧滑)，为打方向盘的速度(角速度)和油门(线速度)。
将控制量参数化

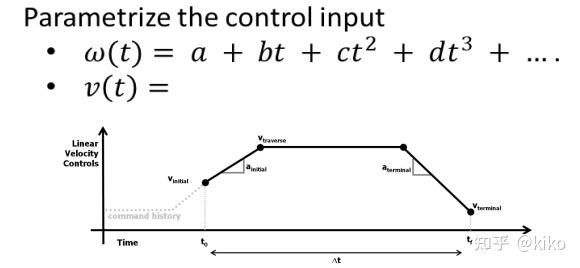
在这里插入图片描述
求解带有约束的轨迹生成，这个就比较麻烦，需要通过数值微分计算雅克比。
这个问题一般就是离线的时候去算最优解，再把搜索出来的lattice graph给在线实时去搜索。

单轮：
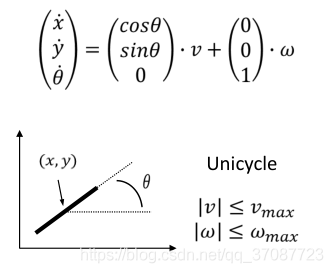
在这里插入图片描述
差动轮

差速机器人有3种运动模式？https://www.jianshu.com/p/5e512065e947

$l$ 为两轮间距
$v_r$ 为右轮速度
$v_l$ 为左轮速度
$r$ 为转弯半径

其中， $r$ 为转弯半径，为线速度比角速度的值：
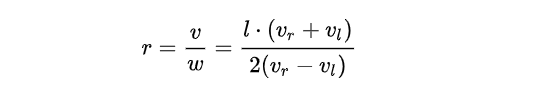
在这里插入图片描述
注意，当左右轮速度接近的时候，r可能会出现无穷大。
====分割线

在这里插入图片描述
简化的汽车模型（图中r应该标记为v）

阿克曼转向几何
转弯中心为啥会在后轴中心线上呢？这是因为车辆就是这么设计的……哈哈哈

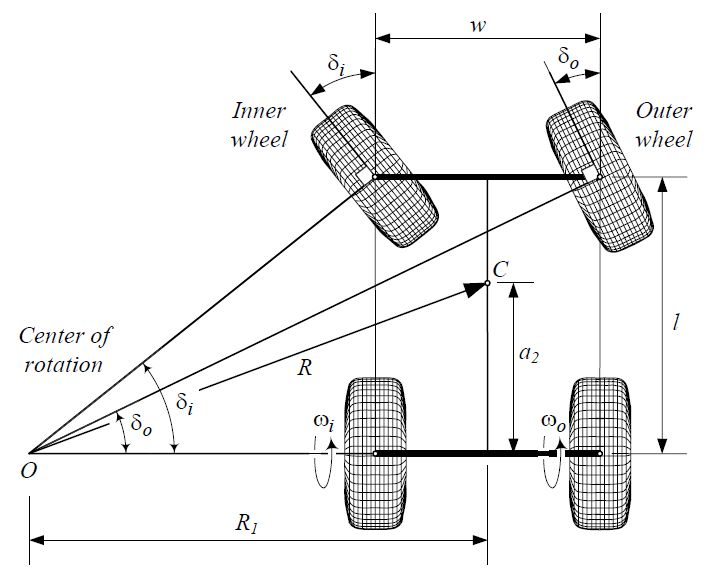
在这里插入图片描述
简化模型：自行车？独轮车？

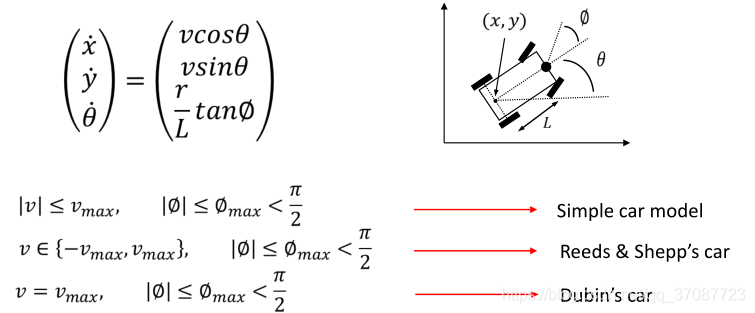
1.3 Hybrid A（基于控制量采样的A搜索）

1.3.1 基本思想

Hybrid A是在A算法的基础上考虑物体实际运动约束的一种算法，核心思想是将三维栅格图搜索和lattice graph结合使用。在搜索过程中，选取不同的control input向前积分，并且永远保持每个栅格中只有一个节点（是否更新节点，取决于待定新节点的损失与原节点的损失哪个更小）。
传统A算法是类似于计算预估代价过程中网格化空间，节点只能沿着节点周边8个方向进行遍历，不考虑运动物体的方向，而且也不考虑物体的运动实际情况，假定物体总能转移到邻近格点中，且物体总是出现在网格中心。但是这并不符合车辆的运动轨迹，所以考虑车辆的运动学特性，提出了Hybrid A算法。在Hybrid A*中考虑物体的方向，在下图中我们用带箭头的点表示一个物体的位置，由于考虑了物体的实际运动约束，所以物体并不一定出现在格点中心（可以出现在每个格中的任意位置，但是每个格内只出现一次）。

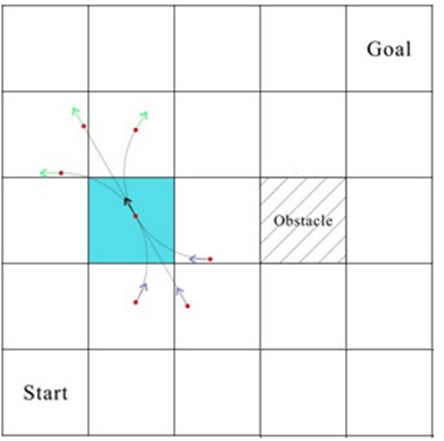
在这里插入图片描述

Hybrid A*算法按照固定的距离，车辆最大转向角度范围内不同的转向角度，向前或者向后遍历节点。由一个特定的位置出发，物体在下一步搜索中只能到达它可能到达的位置。例如在汽车中，受制于汽车转向角的限制，绿色箭头表示车辆前进时候可以到达的位置，灰色箭头表示倒退时可以到达的位置。

Hybrid A*算法只是比较粗的离散化方式遍历，如果仅依靠遍历节点同时满足终点x，y，heading的要求，是很难遍历到的。所以还需要连续空间算法将遍历节点与终点连接。在每次遍历过程中使用ReedShepp曲线将遍历节点与终点连接。（在扩展方式中添加ReedShepp搜索）。其中，Reeds-Shepp 曲线是一种路径规划方法，假设车辆能够以固定的半径转向，且车辆能够前进和后退，那么Reeds-Shepp曲线就是车辆在上述条件下从起点到终点的最短路径。该曲线不仅能保证车辆能够到达终点，而且能保证车辆的角度能在终点到达预期角度。

最终，Hybird A*最终生成的路径是由两部分拼接得到的：从起点按照运动模式搜索（按照角度离散）搜索路径与RS曲线路径（需要离散）。