首先我们回顾一下Gradient Boosting 的本质,就是训练出,使损失函数最小,即
其求解步骤如下:
所以,我们首先得定义出损失函数,才能谈求解的事情。接下来我们针对不同场景,介绍相应的损失函数。
回归
对于回归问题,定义好损失函数后,Gradient Boosting 不需要作出什么修改,计算出来的结果就是预测值。
平方损失
在实际回归中,最常用的之一,就是平方损失,即
将它画出来,形状大致如下
能看出来,它含义就是对较大的偏差有着很强的惩罚,并相对忽略较小的偏差。容易得到,的梯度为
因此代入Algorithm 1,就有了将平方损失应用于Gradient Boosting 的 LS_Boost 方法,步骤如下
绝对值损失
绝对值损失的定义,以及其梯度如下:
绝对值损失函数画出来图,形状如下
有了以上两项(损失函数与梯度),本质上就能够解Algorithm 1了。同时,如果将弱学习算法设为决策树,还能进一步推导出形式更简洁的算法形式。这部分公式推导,此处不再赘述,有兴趣的同学可以参看原文。绝对值损失的 GBDT 算法流程如下
需要了解的是,使用绝对值损失,一般比平方损失更加稳健。
Huber 损失
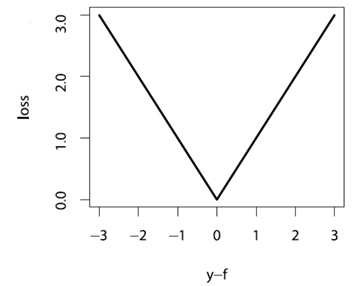
还有一种叫Huber 损失,其定义为
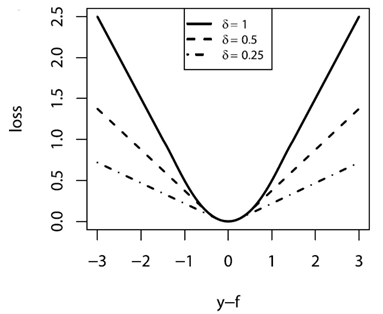
分段函数看起来不直观,它的图画出来大致是
从图和公式可以看出,它融合了平方损失和绝对值损失。当偏差较小时,采用平方差损失;当偏差较大时,采用绝对值损失;而参数就是用于控制偏差的临界值的。
按照作者的说法,对于正态分布的数据,Huber 损失的效果近似于平方差损失;而对于长尾数据,Huber 损失的效果近似于绝对值损失;而对于中等程度拖尾的数据,Huber 损失的效果要优于以上两者。
与平方差损失一样,如果将弱学习算法设为决策树,还能进一步推导出更具体的算法形式,即,Huber 损失的 GBDT 算法流程如下
三种损失函数与对应的梯度表
分类
在说明分类之前,我们先介绍一种损失函数。与常见的直接求预测与真实值的偏差不同,这种损失函数的目的是最大化预测值为真实值的概率。这种损失函数叫做对数损失函数(Log-Likehood Loss),定义如下
对于二项分布,,我们定义预测概率为,即二项分布的概率,可得
即,可以合并写成
对于与的关系,我们定义为
即,。当,;当,
两类分类
对于两类分类,,我们先将它转成二项分布,即令。
于是根据上面得到的,损失函数期望为
其中,定义为
接下来求出梯度
这样,Gradient Boosting 需要的条件就准备齐了。
但是,如果我们将弱算法设置为决策树,并在求解步长的时候利用牛顿法,原算法能够得到如下更简洁的形式,即两类分类的 GBDT 算法流程如下
最后依据计算出来的分类即可。即,通过估算预测的概率
然后根据以下准则预测标签,其中是代价函数,表示当真实类别为,预测类别为时的代价
多类分类
模仿上面两类分类的损失函数,我们能够将类分类的损失函数定义为
其中,,且将与关系定义为
或者,换一种表达方式
接下来求出梯度
于是可以看出,这里在每一次迭代,都要求个参数,和对应的。而求出的则可以理解为属于第类而不是其他类的概率。本质上就是OneVsRest的思想。
同上,如果我们对弱算法选择决策树,则有类分类的 GBDT 算法流程为
然后,根据上面的公式,将最终得到的转换为对应的类别概率,并用于分类即可。分类准则如下
其中,是代价函数,表示当真实类别为,预测类别为时的代价
正则化
采取以上算法去训练测试样本集,能很好地拟合测试数据,相对不可避免地会产生过拟合。为了减少过拟合,可以从两个方面入手,即弱算法的个数,以及收缩率。
弱算法的个数
在推导 AdaBoost 的时候,我们就介绍过,我们希望训练出的是若干个弱算法的线性组合,即
因此,这个的大小就影响着算法的复杂度。
一般来说,在训练阶段,我们通过交叉验证的方式,选择使损失最小的,并用于测试。
收缩率
前面介绍过,在第次迭代时,我们用如下公式更新
而增加收缩率后,则更新公式变为
即越往后训练出的弱算法,其在总算法中占得权重相对越低,于是真正有效的弱算法也就前面有限个,因而影响了算法的复杂度。
同样,在训练阶段,我们通过交叉验证的方式,选择使损失最小的,并用于测试。
不过,和是会相互影响的,一般减小,则对应的最优的会增加。因此,在选择参数时,应该综合考虑这两个参数的效果。
尾巴
在这一部分,我们看到不论在分类还是回归的Gradient Boosting,如果弱算法选择决策树,都能够一定程度简化求解思路;同时,决策树是个简单容易实现的弱算法,在实际中 GBDT 的表现也很好,相反太强太稳定的算法反而容易过拟合。希望这两篇文章不仅能帮助大家了解 GBDT 这类算法,更多的是能了解它整个演化的过程,对它有个更深的理解。








 本文深入探讨了GradientBoosting(GBDT)算法在回归与分类任务中的应用,详细介绍了平方损失、绝对值损失及Huber损失等多种损失函数,并讨论了它们在GBDT中的具体实现过程。此外,文章还介绍了如何通过正则化手段来防止过拟合。
本文深入探讨了GradientBoosting(GBDT)算法在回归与分类任务中的应用,详细介绍了平方损失、绝对值损失及Huber损失等多种损失函数,并讨论了它们在GBDT中的具体实现过程。此外,文章还介绍了如何通过正则化手段来防止过拟合。
 ,使损失函数
,使损失函数 最小,即
最小,即
 所以,我们首先得定义出损失函数
所以,我们首先得定义出损失函数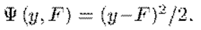
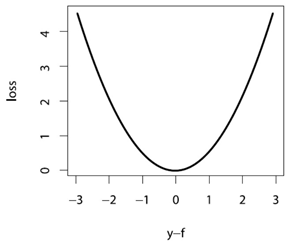 能看出来,它含义就是对较大的偏差有着很强的惩罚,并相对忽略较小的偏差。容易得到,
能看出来,它含义就是对较大的偏差有着很强的惩罚,并相对忽略较小的偏差。容易得到,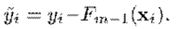 因此代入Algorithm 1,就有了将平方损失应用于Gradient Boosting 的 LS_Boost 方法,步骤如下
因此代入Algorithm 1,就有了将平方损失应用于Gradient Boosting 的 LS_Boost 方法,步骤如下
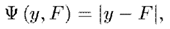
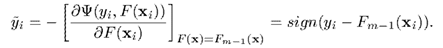

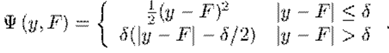
 就是用于控制偏差的临界值的。
就是用于控制偏差的临界值的。


 ,我们定义预测概率为
,我们定义预测概率为 ,即二项分布的概率,可得
,即二项分布的概率,可得
 与
与 的关系,我们定义为
的关系,我们定义为
 。当
。当 ,
, ;当
;当 ,
,
 ,我们先将它转成二项分布
,我们先将它转成二项分布 。
。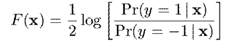
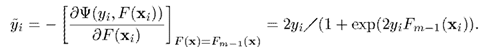

 分类即可。即,通过
分类即可。即,通过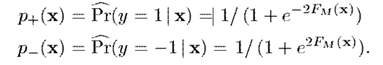
 是代价函数,表示当真实类别为
是代价函数,表示当真实类别为 ,预测类别为
,预测类别为 时的代价
时的代价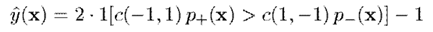
 类分类的损失函数定义为
类分类的损失函数定义为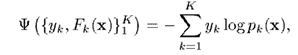
 ,且将
,且将 与
与 关系定义为
关系定义为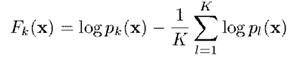
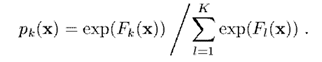 接下来求出梯度
接下来求出梯度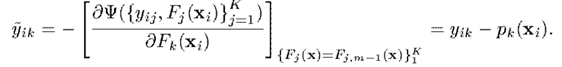
 属于第
属于第 类而不是其他类的概率。本质上就是OneVsRest的思想。
类而不是其他类的概率。本质上就是OneVsRest的思想。
 转换为对应的类别概率
转换为对应的类别概率 ,并用于分类即可。分类准则如下
,并用于分类即可。分类准则如下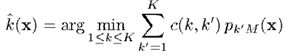
 是代价函数,表示当真实类别为
是代价函数,表示当真实类别为 ,预测类别为
,预测类别为 ,以及收缩率
,以及收缩率 。
。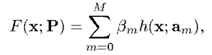
 次迭代时,我们用如下公式更新
次迭代时,我们用如下公式更新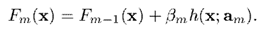
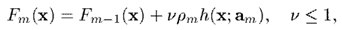
















 6827
6827

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








