【C++/Python】轻松掌握——杨辉三角问题

前言：本篇将讲解关于杨辉三角的问题，主要采用c++和python来进行杨辉三角的代码编写

目录

一、什么是杨辉三角

二、分析杨辉三角

三、代码编写

3.1 前部分

3.2 后部分

---

一、什么是杨辉三角

杨辉三角是一个经典的数学概念，用来描述一个二项式系数的三角形，其中每一行都是上一行的两个相邻数之和。

首先可以看一张动态图，这里非常清晰的显示了杨辉三角：

 

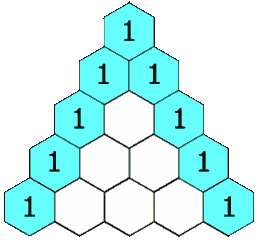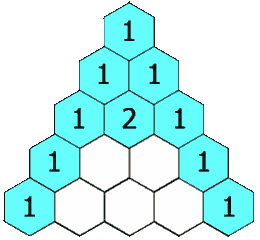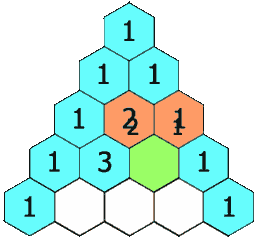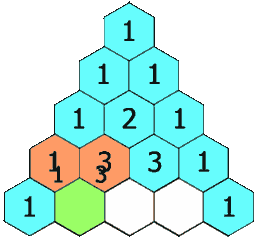
二、分析杨辉三角

1、首先杨辉三角的第一个和最后一个数字都是1

2、除第一个和最后一个数字其余数字都是上面的一个和前一个的数字之和

3、第一行有一个元素，第二行有两个元素，第三行有三个元素一次类推，第n行有n个元素

通过以上分析，我们可以总结一点就是，在C++中我们可以通过二维数组去存储行和列。

三、代码编写

3.1 前部分

首先看，第一行第一个元素是1，可以写一个二维数组，最外面的数组表示行，也就是第几行，里面的数组表示列，第几列。

可以看出，第几行就有几列元素。并且每一行的第一列和最后一列都是1，由此我们可以先将每一行的第一列和最后一列都写成1：

#include <bits/stdc++.h> //导入万能头文件
using namespace std;   
int main(){
	int a[10][10];    //定义一个二维数组
    //第一个for循环表示行
	for (int i=0;i<10;i++){
        //第二个for循环表示列
		for (int j=0;j<=i;j++){
			if (j==0 || j==i){   //如果是第一个元素/最后一个元素就将他存为1
				a[i][j]=1;
			}
		}
	}
	return 0;
}

从上面的代码很容易看出，首先我们定义了一个二维数组，第一层for循环用来表示一共有10行数据，第二个for循环表示每一行一共的列数（元素），每一行的元素最大只有行数那么多，所以只用循环到i就行了（其中由于下标数少一，所以就可以j<=i）。

当我们的j等于0时，也就是那一行的第一列元素或者最后一列元素的时候，就将它赋值为1。

3.2 后部分

现在我们已经成功处理好第一列和最后一列了，我们需要开始处理中间的数据了。

首先分析，我们要处理中间的数据，就需要找到上一行的数据，通过二维数组的存储，我们可以很好的找到上一组的数据，也就是这i行的第j列的数据就等于i-1行的第j列的数据加上第i-1行的第j-1的数据，也就是：a[i][j]=a[i-1][j]+a[i-1][j-1]。

通过分析，我们可以开始写代码了。

#include <bits/stdc++.h> //导入万能头文件
using namespace std;   
int main(){
	int a[10][10];    //定义一个二维数组
    //第一个for循环表示行
	for (int i=0;i<10;i++){
        //第二个for循环表示列
		for (int j=0;j<=i;j++){
			if (j==0 || j==i){   //如果是第一个元素/最后一个元素就将他存为1
				a[i][j]=1;
			}
            else{
				a[i][j]=a[i-1][j]+a[i-1][j-1];   //计算中间数据
			}
			cout<<a[i][j]<<' ';     //输出第i行第j列的元素
		}
		cout<<endl;   //进行换行
	}
	return 0;
}

由此，我们就完成了杨辉三角的C++写法。

对于python而言我们可以采用同样的思路进行编写，代码如下：

lst=[]   # 创建空列表
# 一共执行10行
for i in range(0,10):
    lst.append([])    #每一行都需要添加一个列表，在列表中再添加元素
    for j in range(0,i+1):
        if (j==0 or j==i):
            lst[i].append(1)
        else:
            lst[i].append(lst[i-1][j]+lst[i-1][j-1])
        print(lst[i][j],end=' ')
    print('\n')