In statistics, Spearman's rank correlation coefficient or Spearman's rho, named after Charles Spearman and often denoted by the Greek letter  (rho) or as
(rho) or as  , is a nonparametric measure of statistical dependence between two variables. It assesses how well the relationship between two variables can be described using a monotonic function. If there are no repeated data values, a perfect Spearman correlation of +1 or −1 occurs when each of the variables is a perfect monotone function of the other.
, is a nonparametric measure of statistical dependence between two variables. It assesses how well the relationship between two variables can be described using a monotonic function. If there are no repeated data values, a perfect Spearman correlation of +1 or −1 occurs when each of the variables is a perfect monotone function of the other.
Spearman's coefficient, like any correlation calculation, is appropriate for both continuous and discrete variables, including ordinal variables.[1][2] Spearman's  and Kendall's
and Kendall's  can be formulated as special cases of a more general correlation coefficient.
can be formulated as special cases of a more general correlation coefficient.
Definition and calculation[edit]
The Spearman correlation coefficient is defined as the Pearson correlation coefficient between the ranked variables.[3]
For a sample of size n, the n raw scores  are converted to ranks
are converted to ranks  , and
, and  is computed from:
is computed from:
-

-
where
 denotes the usual Pearson correlation coefficient, but applied to the rank variables.
denotes the usual Pearson correlation coefficient, but applied to the rank variables. is the covariance of the rank variables.
is the covariance of the rank variables. and
and  are the standard deviations of the rank variables.
are the standard deviations of the rank variables.
-
where
Only if all n ranks are distinct integers, it can be computed using the popular formula
-

-
where
 , is the difference between the two ranks of each observation.
, is the difference between the two ranks of each observation.- n is the number of observations
-
where
Identical values are usually each assigned fractional ranks equal to the average of their positions in the ascending order of the values, which is equivalent to averaging over all possible permutations.
If ties are present in the data set, this equation yields incorrect results: Only if in both variables all ranks are distinct, then  (cf. tetrahedral number
(cf. tetrahedral number 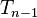 ). The first equation—normalizing by the standard deviation—may even be used even when ranks are normalized to [0;1] ("relative ranks") because it is insensitive both to translation and linear scaling.
). The first equation—normalizing by the standard deviation—may even be used even when ranks are normalized to [0;1] ("relative ranks") because it is insensitive both to translation and linear scaling.
This method should also not be used in cases where the data set is truncated; that is, when the Spearman correlation coefficient is desired for the top X records (whether by pre-change rank or post-change rank, or both), the user should use the Pearson correlation coefficient formula given above.[citation needed]
The standard error of the coefficient (σ) was determined by Pearson in 1907 and Gosset in 1920. It is
- Sort the data by the first column (
 ). Create a new column
). Create a new column  and assign it the ranked values 1,2,3,...n.
and assign it the ranked values 1,2,3,...n. - Next, sort the data by the second column (
 ). Create a fourth column
). Create a fourth column 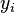 and similarly assign it the ranked values 1,2,3,...n.
and similarly assign it the ranked values 1,2,3,...n. - Create a fifth column
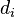 to hold the differences between the two rank columns (
to hold the differences between the two rank columns ( and
and 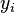 ).
). - Create one final column
 to hold the value of column
to hold the value of column 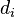 squared.
squared. -


Example[edit]
In this example, the raw data in the table below is used to calculate the correlation between the IQ of a person with the number of hours spent in front of TV per week.
IQ,  | Hours of TV per week,  |
| 106 | 7 |
| 86 | 0 |
| 100 | 27 |
| 101 | 50 |
| 99 | 28 |
| 103 | 29 |
| 97 | 20 |
| 113 | 12 |
| 112 | 6 |
| 110 | 17 |
Firstly, evaluate  . To do so use the following steps, reflected in the table below.
. To do so use the following steps, reflected in the table below.
IQ,  | Hours of TV per week,  | rank  | rank 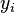 | 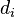 |  |
| 86 | 0 | 1 | 1 | 0 | 0 |
| 97 | 20 | 2 | 6 | −4 | 16 |
| 99 | 28 | 3 | 8 | −5 | 25 |
| 100 | 27 | 4 | 7 | −3 | 9 |
| 101 | 50 | 5 | 10 | −5 | 25 |
| 103 | 29 | 6 | 9 | −3 | 9 |
| 106 | 7 | 7 | 3 | 4 | 16 |
| 110 | 17 | 8 | 5 | 3 | 9 |
| 112 | 6 | 9 | 2 | 7 | 49 |
| 113 | 12 | 10 | 4 | 6 | 36 |
With  found, add them to find
found, add them to find  . The value of n is 10. These values can now be substituted back into the equation :
. The value of n is 10. These values can now be substituted back into the equation : to give
to give
which evaluates to ρ = -29/165 = −0.175757575... with a P-value = 0.627188 (using the t distribution)
This low value shows that the correlation between IQ and hours spent watching TV is very low, although the negative value suggests that the longer the time spent watching television the lower the IQ. In the case of ties in the original values, this formula should not be used; instead, the Pearson correlation coefficient should be calculated on the ranks (where ties are given ranks, as described above).
皮尔森相关系数
皮尔森相关系数(Pearson correlation coefficient)也叫皮尔森积差相关系数(Pearson product-moment correlation coefficient),是用来反应两个变量相似程度的统计量。或者说可以用来计算两个向量的相似度(在基于向量空间模型的文本分类、用户喜好推荐系统中都有应用)。
皮尔森相关系数计算公式如下:
ρX,Y=cov(X,Y)σXσY=E((X−μX)(Y−μY))σXσY=E(XY)−E(X)E(Y)E(X2)−E2(X)√E(Y2)−E2(Y)√ ρX,Y=cov(X,Y)σXσY=E((X−μX)(Y−μY))σXσY=E(XY)−E(X)E(Y)E(X2)−E2(X)E(Y2)−E2(Y)
分子是协方差,分子是两个变量标准差的乘积。显然要求X和Y的标准差都不能为0。
当两个变量的线性关系增强时,相关系数趋于1或-1。正相关时趋于1,负相关时趋于-1。当两个变量独立时相关系统为0,但反之不成立。比如对于
y=x2
y=x2,X服从[-1,1]上的均匀分布,此时E(XY)为0,E(X)也为0,所以
ρX,Y=0
ρX,Y=0,但x和y明显不独立。所以“不相关”和“独立”是两回事。当Y 和X服从联合正态分布时,其相互独立和不相关是等价的。
对于居中的数据来说(何谓居中?也就是每个数据减去样本均值,居中后它们的平均值就为0),E(X)=E(Y)=0,此时有:
ρX,Y=E(XY)E(X2)√E(Y2)√=1N∑Ni=1XiYi1N∑Ni=1X2i√1N∑Ni=1Y2i√=∑Ni=1XiYi∑Ni=1X2i√∑Ni=1Y2i√=∑Ni=1XiYi||X||||Y|| ρX,Y=E(XY)E(X2)E(Y2)=1N∑i=1NXiYi1N∑i=1NXi21N∑i=1NYi2=∑i=1NXiYi∑i=1NXi2∑i=1NYi2=∑i=1NXiYi||X||||Y||
即相关系数可以看作是两个随机变量中得到的样本集向量之间夹角的cosine函数。
进一步当X和Y向量归一化后,||X||=||Y||=1,相关系数即为两个向量的乘积 ρX,Y=X∙Y ρX,Y=X∙Y。
Spearman秩相关系数
首先说明秩相关系数还有其他类型,比如kendal秩相关系数。
使用Pearson线性相关系数有2个局限:
- 必须假设数据是成对地从正态分布中取得的。
- 数据至少在逻辑范围内是等距的。
对于更一般的情况有其他的一些解决方案,Spearman秩相关系数就是其中一种。Spearman秩相关系数是一种无参数(与分布无关)检验方法,用于度量变量之间联系的强弱。在没有重复数据的情况下,如果一个变量是另外一个变量的严格单调函数,则Spearman秩相关系数就是+1或-1,称变量完全Spearman秩相关。注意这和Pearson完全相关的区别,只有当两变量存在线性关系时,Pearson相关系数才为+1或-1。
对原始数据xi,yi按从大到小排序,记x'i,y'i为原始xi,yi在排序后列表中的位置,x'i,y'i称为xi,yi的秩次,秩次差di=x'i-y'i。Spearman秩相关系数为:
ρs=1−6∑d2in(n2−1) ρs=1−6∑di2n(n2−1)
| 位置 | 原始X | 排序后 | 秩次 | 原始Y | 排序后 | 秩次 | 秩次差 |
| 1 | 12 | 546 | 5 | 1 | 78 | 6 | 1 |
| 2 | 546 | 45 | 1 | 78 | 46 | 1 | 0 |
| 3 | 13 | 32 | 4 | 2 | 45 | 5 | 1 |
| 4 | 45 | 13 | 2 | 46 | 6 | 2 | 0 |
| 5 | 32 | 12 | 3 | 6 | 2 | 4 | 1 |
| 6 | 2 | 2 | 6 | 45 | 1 | 3 | -3 |
对于上表数据,算出Spearman秩相关系数为:1-6*(1+1+1+9)/(6*35)=0.6571
查阅秩相关系数检验的临界值表
| n | 显著水平 | |
| 0.01 | 0.05 | |
| 5 | 0.9 | 1 |
| 6 | 0.829 | 0.943 |
| 7 | 0.714 | 0.893 |
n=6时,0.6571<0.829,所以在0.01的显著水平下认为X和Y是不相关的。
如何原始数据中有重复值,则在求秩次时要以它们的平均值为准,比如:
| 原始X | 秩次 | 调整后的秩次 |
| 0.8 | 5 | 5 |
| 1.2 | 4 | (4+3)/2=3.5 |
| 1.2 | 3 | (4+3)/2=3.5 |
| 2.3 | 2 | 2 |
| 18 | 1 | 1 |
Spearman秩相关系数应该是从秩和检验延伸过来的,因为它们很像。
相关性和相似度的区别
X=(1,2,3)跟Y=(4,5,6)的皮尔森相关系数等于1,说明X和Y是严格线性相关的(事实上Y=X+3)。
但是X和Y的相似度却不是1,如果用余弦距离来度量,X和Y之间的距离明显大于0。























 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










