在前面的手写数字案例中,权重是人为指定的,工作量大,具有太大的主观性。能否让程序从数据中自动学习特征,实现自动获取最优权重。就要用到神经网络的学习。
1、从数据中学习
机器学习从数据中学习规律,模式,深度学习则比机器学习更能避免人为介入。
比如要实现数字5的识别:

但是数字5的写法五花八门,程序要发现其中规律还是很困难的。
为了解决这个问题,两种方案:
方案1:先从图像中提取特征量,再用机器学习技术学习这些特征量的模式。
特征量:可以从输入数据/图像中准确提取本质数据的转换器。
常用的特征量包括SIFT、SURF和HOG等,使用特征量将图像数据转换为向量,然后对转换后的向量使用SVM、KNN等分类器进行学习。
缺点:需要人工设计特征量;识别任务更换后,特征量也要重新设计。
深度学习是将图片输入,由算法提取特征量。
方案2:神经网络或深度学习提取特征量。
优点:所有问题都可以采用同样的流程,实现端对端的学习。
端对端(end-to-end):从原始数据(输入)中获取目标结果(输出)的过程。
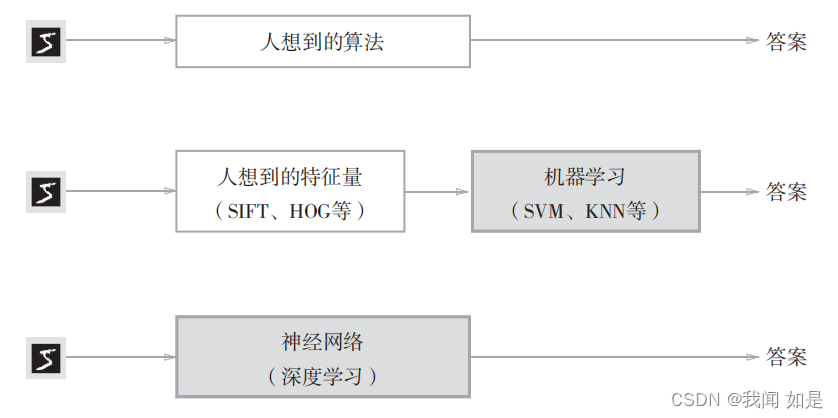
图1 人工设计规律到从数据学习
1.1 训练数据和测试数据
为了提高模型的泛化能力,必须将数据划分为训练集和测试集。
泛化能力:处理未被观察过的数据的能力。
获得泛化能力是机器学习的最终目标。当然对某个数据集过度拟合就会出现过拟合。
避免过拟合也是机器学习的重要课题。
2、损失函数(loss function)
神经网络的学习通过某个指标表示现在的状态,然后以这个指标为基准,寻找最优权重参数。神经网络学习中所用的这个指标为损失函数。一般用均方误差和交叉熵误差。
损失函数表示神经网络性能的“恶劣程度”的指标。即网络对数据再多大程度上不拟合。
2.1 均方误差(mean squared error)
(1-1)
其中:
y为神经网络的输出;
t为监督数据,
k为维数。
比如:10个元素
y=[0.1,0.05,0.6,0,0.05,0.1,0,0.1,0,0]
t=[0,0,1,0,0,0,0,0,0,0]
通过softmax函数后变为概率,即0的概率为0.1,1的概率为0.05,2的概率为0.6等
这种表示方法称为one-hot表示。即只有正确标签为1,其余标签都为0的表示方法。
在程序中加载数据的时候,使用one_hot_label=True,就是one-hot表示。
(x_train,t_train),(x_test,t_test) = load_mnist(normalize=True,flatten=True,one_hot_label=True)
实现方法:
def mean_squared_error(y,t):
returen 0.5*np.sum((y-t)**2)
例1:
t=[0,0,1,0,0,0,0,0,0,0]
y=[0.1,0.05,0.6,0,0.05,0.1,0,0.1,0,0]
mean_squared_error(np.array(y),np.array(t))
t标签为2,y2的概率也是最高。均值误差0.0975。
例2:正确标签为2,预测为7
t=[0,0,1,0,0,0,0,0,0,0]
y=[0.1,0.05,0.1,0,0.05,0.1,0,0.6,0,0]
mean_squared_error(np.array(y),np.array(t))
计算结果0.5975。
例1的误差较小,即输出结果与监督数据更加吻合。
2.2 交叉熵误差(cross entropy error)
(1-2)
交叉熵误差的值是由正确解标签对应的输出结果决定。
代码实现:
def cross_entropy_error(y,t):
delta=1e-7
return -np.sum(t*np.log(y+delta))
添加一个delta微小值可以防止负无限大的发生。
重复上面的例子
t=[0,0,1,0,0,0,0,0,0,0]
y=[0.1,0.05,0.6,0,0.05,0.1,0,0.1,0,0]
cross_entropy_error(np.array(y),np.array(t))
输出为0.51.
t=[0,0,1,0,0,0,0,0,0,0]
y=[0.1,0.05,0.1,0,0.05,0.1,0,0.6,0,0]
cross_entropy_error(np.array(y),np.array(t))
输出为2.3.
2.3 mini-batch学习
前面的介绍中只考虑是针对单个数据的损失函数。如果需要对N个数据进行计算,就要对前面的公式(1-1)和(1-2)除以N,即求数据的“平均损失函数”。但是如果数据量达到成百上千万,计算平均值计算量太大。所以从数据中选出一批数据(mini-batch,小批量)作为全部数据的近似,然后对mini-batch学习。这种方法称为mini-batch学习。
mini-batch版交叉熵误差实现代码:
def cross_entropy_error(y,t):
if y.dim==1:
t=t.reshape(1,t.size)
y=y.reshape(1,y.size)
batch_size=y.shape[0]
return -np.sum(t*np.log(y+1e-7))/batch_size
当监督数据为非ont-hot表示时,代码如下:
def cross_entropy_error(y,t):
if y.ndim==1:
t=t.reshape(1,t.size)
y=y.reshape(1,y.size)
batch_size=y.shape[0]
return -np.sum(np.log(y[np.arange(batch_size),1]+1e-7))/batch_size
2.4 为什么要设定损失函数?
既然目标是提高精度,为什么不把精度作为指标?
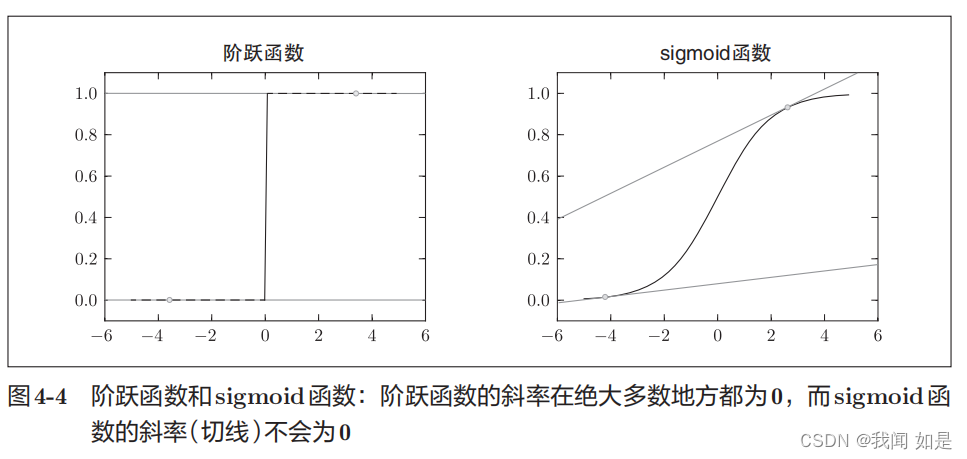
1、因为要去求最小值,需要求函数的导数。不用精度作为指标,是因为精度导数很多为0,导致参数无法更新。
2、精度微调参数,精度变化很小,有变化也会变成不连续、离散的值,而损失函数可以发生连续性的变化。
神经网络不使用阶跃函数作为激活函数,也是同样的道理。
 神经网络学习与损失函数
神经网络学习与损失函数





 本文介绍了机器学习中从数据中学习规律、使用特征量如SIFT、SURF和HOG进行图像分析,以及神经网络通过损失函数如均方误差和交叉熵优化权重参数的过程。讨论了训练数据、测试数据划分、过拟合问题和随机梯度下降法在mini-batch学习中的应用。
本文介绍了机器学习中从数据中学习规律、使用特征量如SIFT、SURF和HOG进行图像分析,以及神经网络通过损失函数如均方误差和交叉熵优化权重参数的过程。讨论了训练数据、测试数据划分、过拟合问题和随机梯度下降法在mini-batch学习中的应用。
















 8万+
8万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








