大数定律 Law of Larger Numbers
X是随机变量,E(X)是期望值。
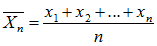 ,X是随机变量,E(X)是期望值。
,X是随机变量,E(X)是期望值。
以X=抛投100个/次fair coin正面的个/次数。当我们不断地抛100次,当抛了无数次100次硬币时,平均每次测试的正面coin就趋向于50。
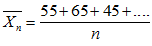 ,当n→∞时, E(X)→50。
,当n→∞时, E(X)→50。
因为每次抛投都是孤立,是不相干的时间,当n趋向无穷时,就趋向50。
 本文探讨了大数定律的基本概念,通过抛掷公平硬币实验解释了期望值的概念。随着试验次数无限增加,正面朝上的硬币数量将趋向于50。这种现象说明了随机变量在大量重复试验中表现出的稳定趋势。
本文探讨了大数定律的基本概念,通过抛掷公平硬币实验解释了期望值的概念。随着试验次数无限增加,正面朝上的硬币数量将趋向于50。这种现象说明了随机变量在大量重复试验中表现出的稳定趋势。
大数定律 Law of Larger Numbers
X是随机变量,E(X)是期望值。
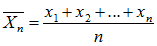 ,X是随机变量,E(X)是期望值。
,X是随机变量,E(X)是期望值。
以X=抛投100个/次fair coin正面的个/次数。当我们不断地抛100次,当抛了无数次100次硬币时,平均每次测试的正面coin就趋向于50。
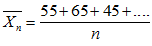 ,当n→∞时, E(X)→50。
,当n→∞时, E(X)→50。
因为每次抛投都是孤立,是不相干的时间,当n趋向无穷时,就趋向50。
 147
147

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


