F. Milk Factory

GDUT 2020寒假训练 排位赛二 F

原题链接

• F. Milk Factory

题目

The milk business is booming! Farmer John’s milk processing factory consists of N processing stations, conveniently numbered 1…N (1≤N≤100), and N−1 walkways, each connecting some pair of stations. (Walkways are expensive, so Farmer John has elected to use the minimum number of walkways so that one can eventually reach any station starting from any other station). To try and improve efficiency, Farmer John installs a conveyor belt in each of its walkways. Unfortunately, he realizes too late that each conveyor belt only moves one way, so now travel along each walkway is only possible in a single direction! Now, it is no longer the case that one can travel from any station to any other station.

However, Farmer John thinks that all may not be lost, so long as there is at least one station i such that one can eventually travel to station i from every other station. Note that traveling to station i from another arbitrary station j may involve traveling through intermediate stations between i and j. Please help Farmer John figure out if such a station i exists.

Input
The first line contains an integer N, the number of processing stations. Each of the next N−1 lines contains two space-separated integers ai and bi with 1≤ai,bi≤N and ai≠bi. This indicates that there is a conveyor belt that moves from station ai to station bi, allowing travel only in the direction from ai to bi.

Output
If there exists a station i such that one can walk to station i from any other station, then output the minimal such i. Otherwise, output −1.

样例

input
3
1 2
3 2
output
2

题目大意

有n个点，和n-1对关系，表示可以从x走到y（单向），求是否存在一个编号最小的点i，使得从任意点出发都可以到达点i，若不存在则输出-1.

思路

之前的思路是并查集，对每一个关系进行合并操作，并将该集合的元素+1

fx=getfa(x);
fy=getfa(y);
if(fx!=fy)
{
	fa[fx]=fy;
	ans[fy]+=ans[fx]+1;
}

ans[i]表示以i为老大的集合的元素个数。
最后从1到n遍历ans数组，找到哪一个集合的元素个数为n-1就输出，都找不到就输出-1。

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<memory.h>
using namespace std;
int fa[200];
int ans[200];
int getfa(int x)
{
	if(fa[x]==x)return x;
	else return fa[x]=getfa(fa[x]);	
}
int main()
{
	int n;
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		fa[i]=i;
	}
	memset(ans,0,sizeof ans);
	for(int i=1;i<=n-1;i++)
	{
		int x,y;
		cin>>x>>y;
		int fx,fy;
		fx=getfa(x);
		fy=getfa(y);
		if(fx!=fy)
		{
			fa[fx]=fy;
			ans[fy]+=ans[fx]+1;
		}
	}
	for(int i=1;i<=n;i++)
	{
		//cout<<ans[i]<<" ";
		if(ans[i]==n-1)
		{
			cout<<i<<endl;
			return 0;
		}
	}
	cout<<-1<<endl;
	return 0;
}

乍一看感觉莫得问题，但是提交就wa。
后来发现，这个并查集在路径压缩的时候将单向边的信息丢失了，也就是同属于一个集合但是并不能通过单向边到达。
比如

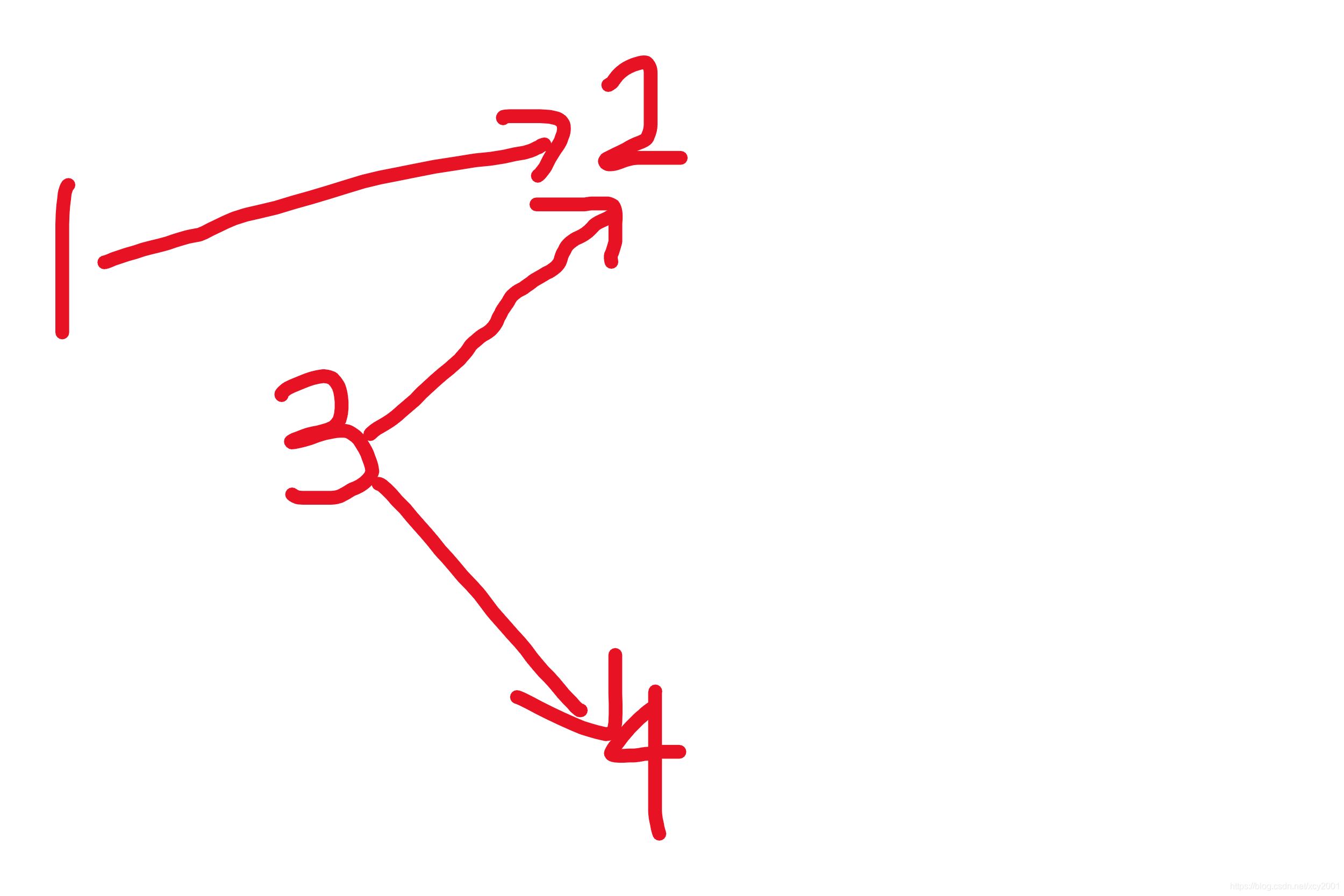
这种情况，按照这个并查集的思路，1 2 3 4 同属于一个集合，而当构建1–>2,3–>2,3–>4这样的关系，输出的是4
当构建1–>2,3–>4,3–>2这样的关系，输出的是2
然而，这种情况不满足题意，也就是不存在这样的点，使得所有点都能到达该点，也就是应该输出-1.
那么通过这个例子发现，这样的并查集忽略了点与点之间的单向边的关系。所以决定采取深搜的办法。
深搜
构建邻接矩阵，对每一个点进行dfs，并在dfs的过程中记录经过点的个数，当经过点的个数与所有的的总数-1相等时输出这个点。

最后代码

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<memory.h>
using namespace std;
bool mp[105][105];
int cnt=0;
int n;
void dfs(int x)
{
	for(int i=1;i<=n;i++)
	{
		if(mp[i][x]==1)
		{
			cnt++;
			dfs(i);
		}
	}
	return ;
}
int main()
{
	cin>>n;
	memset(mp,false,sizeof mp);
	for(int i=1;i<=n-1;i++)
	{
		int x,y;
		cin>>x>>y;
		mp[x][y]=1;
	}
	for(int i=1;i<=n;i++)
	{
		cnt=0;
		dfs(i);
		if(cnt==n-1)
		{
			cout<<i<<endl;
			return 0;
		}
	}
	cout<<-1<<endl;
	return 0;
}