动态规划 - 编辑距离 && 不同的子序列

目录

1. 编辑距离

1.1 题目描述

1.2 解题思路

1.3 画图分析

1.4 代码示例

2. 不同的子序列

2.1 题目描述

2.2 解题思路

2.4 代码优化

---

1. 编辑距离

1.1 题目描述

给定两个单词word1和word2，请计算将word1转换为word2至少需要多少步操作。
你可以对一个单词执行以下3种操作：
a）在单词中插入一个字符
b）删除单词中的一个字符
c）替换单词中的一个字符

示例1

输入："b",""
返回值：1

示例2

输入："ab","bc"
返回值：2

1.2 解题思路

问题: word1 到 word2 的编辑距离 (两个字符串之间, 由一个转成另一个所需的最少编辑次数)

子问题: word1 的局部变成 word2 局部所需要的编辑距离.

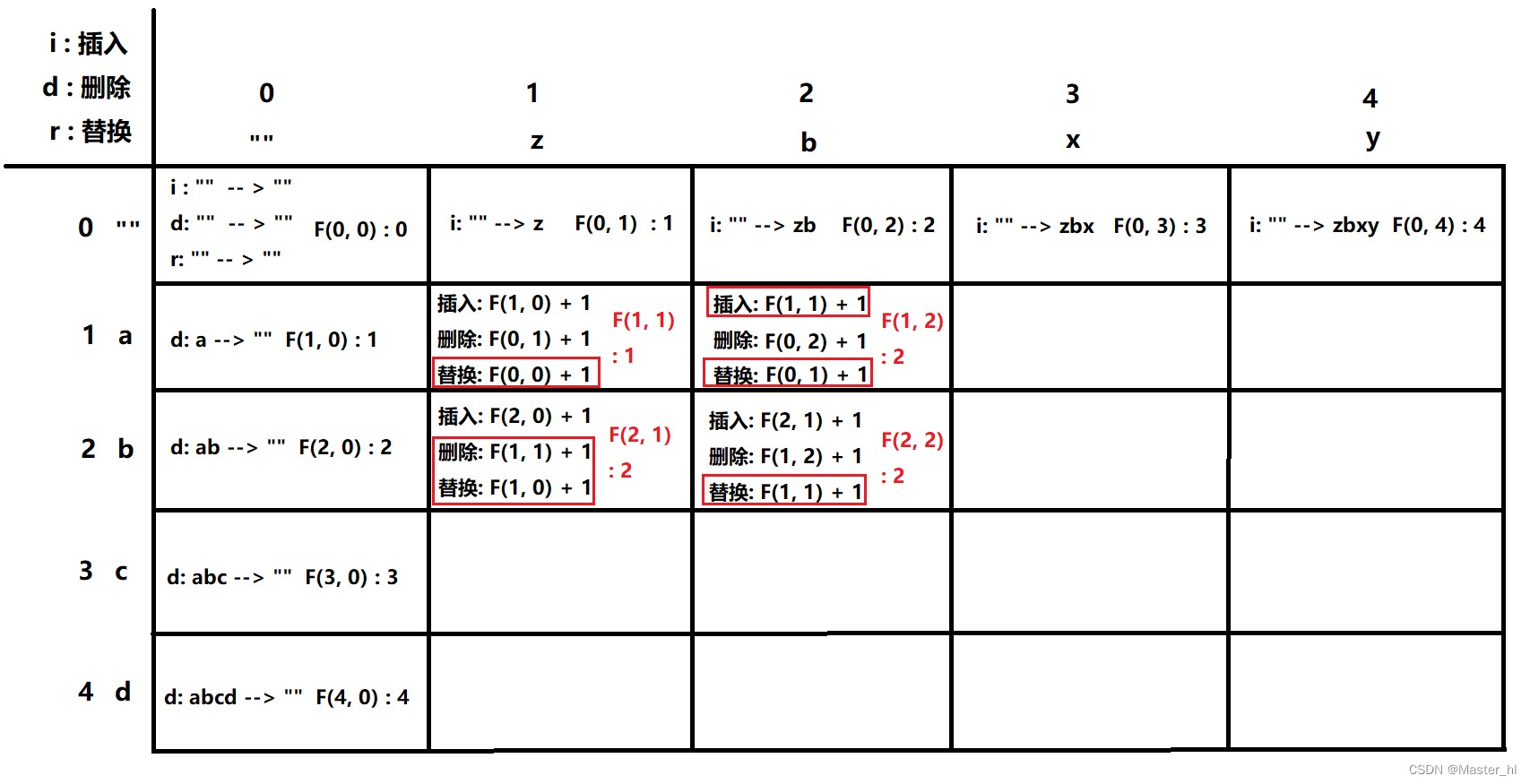
状态定义 F(i, j): word1 前 i 个字符转成 word2 前 j 个字符的编辑距离.

状态转移方程: F(i, j) = min(插入, 删除, 替换)

        F(i, j) = min(F(i - 1, j) + 1, F(i, j - 1) + 1,

                                        F(i - 1, j - 1) + (word1.charAt(i) == word2.charAt(j)) ? 0 : 1)

        我们只需要从删除,替换,插入三个操作中选一个编辑距离最小的, 而替换又分两种情况, 

        当 字符 i 和 字符 j 刚好相等的时候, 就不需要替换, 也就是不需要 + 1. 

初始状态: F(i ,0) = i,   F(0, j) = j

返回结果: F(row,  col)

1.3 画图分析

 

1.4 代码示例

    public int minDistance (String word1, String word2) {
        if (word1 == null && word2 == null) {
            return 0;
        }
        int row = word1.length();
        int col = word2.length();
        int[][] dp = new int[row + 1][col + 1];
        // 初始状态 F(i, 0) = i;
        for (int i = 1; i <= row; i++) {
            dp[i][0] = i;
        }
        // 初始状态 F(0, j) = j
        for (int j = 1; j <= col; j++) {
            dp[0][j] = j;
        }
        for (int i = 1; i <= row; i++) {
            for (int j = 1; j <= col; j++) {
                // 状态转移方程 : F(i ,j) = min(F(i - 1, j) + 1, F(i, j - 1) + 1, F(i - 1, j -1) + (word1.charAt(i) == word2.charAt(j)) ? 0 : 1))
                // 删除, 插入
                dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + 1;
                // 替换 -- 如果两字符相等, 则不需要替换
                if (word1.charAt(i - 1) == word2.charAt(j - 1)) {
                    dp[i][j] = Math.min(dp[i][j], dp[i - 1][j - 1]);
                } else {
                    dp[i][j] = Math.min(dp[i][j], dp[i - 1][j - 1] + 1);
                }
            }
        }
        return dp[row][col];
    }

2. 不同的子序列

2.1 题目描述

给定两个字符串S和T，返回S子序列等于T的不同子序列个数有多少个？
字符串的子序列是由原来的字符串删除一些字符（也可以不删除）
在不改变相对位置的情况下的剩余字符（例如，"ACE"is a subsequence of"ABCDE"但是"AEC"不是）
例如：
S="nowcccoder", T = "nowccoder"
返回3

示例1

输入："nowcccoder","nowccoder"
返回值：3

2.2 解题思路

问题:  S 中与 T 相同的子序列的个数.

子问题:  S 的子串中, 与 T 相同的子序列个数.

状态定义 F(i, j):  S 的前 i 个字符构成的子串中, 与 T 的前 j 个字符相同的子序列个数.

状态转移方程: 

    当 S.charAt(i) == T.charAt(j) 时:    F(i, j)  =  F(i - 1, j - 1) + F(i - 1, j)

• 如果使用第 i 个字符, 那么就只能作为子序列的最后一个字符, 相当于是和 T 的第 j 个字符进行匹配     F(i, j)  =  F(i - 1, j - 1)
• 如果不使用第 i 个字符,  那么就需要从 S 的前 i - 1 个字符构成的字符串中寻找和 T 的前 j 个字符相同的子序列    F(i, j)  =  F(i - 1, j)

    当 S.charAt(i) != T.charAt(j) 时:    F(i, j)  =  F(i - 1, j)    (等同于不使用第 i 个字符的情况)

初始状态:  F(i, 0) = 1 (第一列),     F(0, j) = 0 (第一行 &&  j != 0)

返回结果: F(row, col)

2.3 代码示例

    public int numDistinct (String S, String T) {
        if (S.length() < T.length()) {
            return 0;
        }
        int row = S.length();
        int col = T.length();
        int[][] dp = new int[row + 1][col + 1];
        // 初始状态: F(i,0) = 1   F(0,j) = 0 (j != 0)
        for (int i = 0; i <= row; i++) {
            dp[i][0] = 1;
        }
        for (int j = 1; j <= col; j++) {
            dp[0][j] = 0;
        }
        // 状态转移方程 :
        // s.charAt(i) == t.charAt(j) --> dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]
        // s.charAt(i) != t.charAt(j) --> dp[i][j] = dp[i - 1][j]
        for (int i = 1; i <= row; i++) {
            for (int j = 1; j <= col; j++) {
                if (S.charAt(i - 1) == T.charAt(j - 1)) {
                    dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
                } else {
                    dp[i][j] = dp[i - 1][j];
                }
            }
        }
        return dp[row][col];
    }

由于 dp[i][j] 只和 dp[i - 1][j],  f[i - 1][j - 1] 有关,  类似于背包问题，可以用一维数组保存上一行的结果，每次从最后一列更新元素值.

2.4 代码优化

    public int numDistinct (String S, String T) {
        if (S.length() < T.length()) {
            return 0;
        }
        int row = S.length();
        int col = T.length();
        int[] dp = new int[col + 1];
        // 初始状态: F(i,0) = 1   F(0,j) = 0 (j != 0)
        dp[0] = 1;
        // 状态转移方程 :
        // s.charAt(i) == t.charAt(j) --> dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]
        // s.charAt(i) != t.charAt(j) --> dp[i][j] = dp[i - 1][j]
        for (int i = 1; i <= row; i++) {
            for (int j = col; j > 0; j--) {
                if (S.charAt(i - 1) == T.charAt(j - 1)) {
                    dp[j] = dp[j - 1] + dp[j];
                }
            }
        }
        return dp[col];
    }

---