Monge-Elkan算法是一种高效的字符串相似度计算方法

Monge-Elkan算法是一种高效的字符串相似度计算方法，特别适用于处理由多个词组成的复杂字符串（如人名、地址、机构名称等）的相似性度量。该算法通过分词后逐词比较，结合编辑距离的归一化相似度计算字符串整体相似度，能够有效处理拼写错误、缩写、词序变化等多种情况。相比简单的编辑距离或余弦相似度，它在保留字符串内部结构的同时，提供了更精确的相似性评估，因此在实体识别、数据清洗、信息检索等领域得到广泛应用。

一、通俗易懂的例子

让我们通过一个简单的地址匹配例子来理解Monge-Elkan算法的工作原理。假设我们有两个地址字符串：

• 地址A: “北京市海淀区中关村大街27号”
• 地址B: “北京海淀中关村大街27号”我们的目标是计算这两个地址的相似度。

按照Monge-Elkan算法的步骤，首先需要将两个地址进行分词处理：

• 地址A分词结果: [“北京”, “市”, “海淀”, “区”, “中关村大街”, “27号”]
• 地址B分词结果: [“北京”, “海淀”, “中关村大街”, “27号”]

接下来，算法会对地址A中的每个词与地址B中的所有词进行比较，并记录每个词的最大相似度：

1. "北京"与地址B中的词比较：
   1. “北京” vs “北京” → 完全匹配，相似度1.0
   2. “北京” vs “海淀” → 编辑距离3（需要删除"北"和"京"，再插入"海"和"淀"），归一化后相似度0.0
2. 最大相似度为1.0"市"与地址B中的词比较：
   1. “市” vs “北京” → 编辑距离3（需要插入"北"和"京"），归一化后相似度0.0
   2. “市” vs “海淀” → 编辑距离4（需要插入"海"和"淀"），归一化后相似度0.0
3. 最大相似度为0.0"海淀"与地址B中的词比较：
   1. “海淀” vs “海淀” → 完全匹配，相似度1.0
4. 最大相似度为1.0"区"与地址B中的词比较：
   1. “区” vs “北京” → 编辑距离3（需要插入"北"和"京"），归一化后相似度0.0
   2. “区” vs “海淀” → 编辑距离4（需要插入"海"和"淀"），归一化后相似度0.0
5. 最大相似度为0.0"中关村大街"与地址B中的词比较：
   1. “中关村大街” vs “中关村大街” → 完全匹配，相似度1.0
6. 最大相似度为1.0"27号"与地址B中的词比较：
   1. “27号” vs “27号” → 完全匹配，相似度1.0

最大相似度为1.0

最后，算法将这些最大相似度值求平均，得到两个地址的整体相似度：

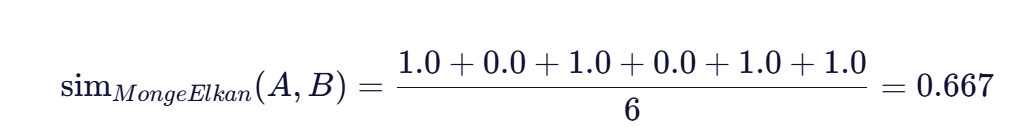
这个结果表明，地址A和地址B有约66.7%的相似度，虽然地址A比地址B多出了两个词（“市"和"区”），但核心部分（“北京”、“海淀”、“中关村大街”、“27号”）完全匹配，因此整体相似度较高。

二、算法原理步骤

Monge-Elkan算法的核心原理可以归纳为以下几个步骤：

步骤1：字符串分词处理

将两个需要比较的字符串拆分为独立的词序列。分词方式可以是空格分隔（适用于英文等自然分词语言），也可以是基于词典的最大匹配分词（适用于中文等无空格分隔的语言）。分词的准确性直接影响最终相似度计算的结果。

步骤2：逐词相似度计算

对第一个字符串中的每个词，计算它与第二个字符串中所有词的相似度。常用的基础相似度函数包括归一化编辑距离、Jaro-Winkler相似度等。对于每个词对，计算其基础相似度值。

步骤3：寻找最佳匹配

对于第一个字符串中的每个词，找到其在第二个字符串中最相似的词（即最大相似度值）。这一步确保了每个词都能找到最接近的对应词，即使词序不同或存在插入/删除操作。

步骤4：相似度平均化

将所有词的最大相似度值求平均，得到两个字符串的整体相似度。平均化处理使相似度结果具有可比性和稳定性，便于后续的相似性判断。

步骤5：结果标准化

将最终相似度值标准化到[0,1]区间，0表示完全不相似，1表示完全匹配。这一步确保了相似度结果的直观性和一致性。通过这种逐词匹配和平均化的方法，Monge-Elkan算法能够有效处理字符串中的局部错误、缩写和词序变化等问题，提供更准确的相似度评估。

三、数学公式与参数解释

Monge-Elkan算法的数学表达式如下：

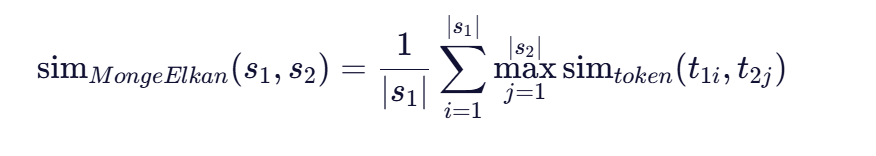其中：

• ( s_1 ) 和 ( s_2 ) 是待比较的两个字符串
• ( |s_1| ) 和 ( |s_2| ) 是分词后的词数量
• ( t_{1i} ) 是字符串 ( s_1 ) 的第 ( i ) 个词
• ( t_{2j} ) 是字符串 ( s_2 ) 的第 ( j ) 个词
• simtoken 是词级相似度函数

关键参数与函数解释：

1. 分词规则（Tokenization）
   1. 分词方式直接影响算法效果，需根据具体语言和应用场景选择合适的分词策略。
   2. 中文常用基于词典的最大匹配分词，英文通常用空格分隔。
   3. 分词粒度（如是否将"北京市"拆分为"北京"和"市"）会影响相似度计算，需权衡考虑。
2. 词级相似度函数（Token Similarity Function）
   1. 归一化编辑距离：最常用的基础相似度函数，计算方式为：

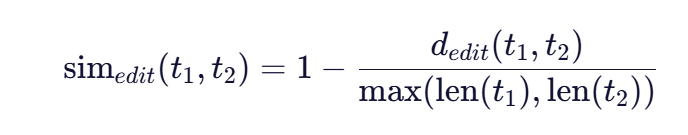
其中 ( d_{edit}(t_1, t_2) ) 是Levenshtein编辑距离（插入、删除、替换操作的最小次数）。

1. 1. Jaro-Winkler相似度：另一种常用词级相似度函数，特别适合短字符串（如人名）的比较，能够处理字符顺序的变化。
   2. 余弦相似度：适用于词向量表示的场景，通过比较词向量的夹角来度量相似度。
2. 归一化编辑距离公式

编辑距离归一化的数学表达式为：

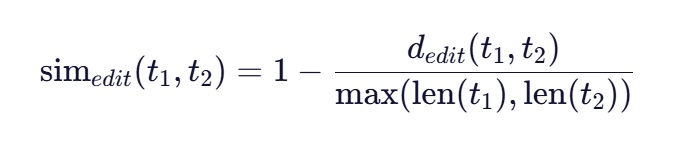
其中：

• dedit (t1 ,t2 ) 是两个词之间的编辑距离
• len(t1 ) 和 len(t2 ) 是两个词的长度

归一化处理确保了相似度值在[0,1]区间内，使不同长度的词之间的相似度具有可比性。

    3.算法复杂度

这种复杂度使其在处理长字符串或大规模数据时可能面临性能挑战，但在实际应用中，通常可以通过预处理（如长度限制、停用词过滤）来优化计算效率。

四、与其他相似度算法的对比

Monge-Elkan算法与其他常见相似度算法相比具有独特优势：

算法名称	适用场景	优点	缺点
编辑距离	短字符串精确匹配	计算简单，结果直观	不考虑词结构，对长字符串效率低
余弦相似度	高维向量空间比较	计算高效，适合大规模数据	不考虑顺序和结构，对局部错误敏感
Jaccard相似度	集合相似性比较	计算简单，适合二进制特征	不考虑词权重和相似度程度
Monge-Elkan	复杂字符串匹配	考虑词结构，处理局部错误和缩写	计算复杂度较高，依赖分词质量

Monge-Elkan算法的核心优势在于它结合了基于词的相似度计算和编辑距离的局部匹配能力，能够有效处理字符串中的局部错误、词序变化和缩写等问题。例如，比较"北京师范大学"和"北京师大"时，它能够识别出"师范大学"和"师大"之间的相似关系，而简单的编辑距离则需要较大的调整才能匹配。

五、实际应用场景

Monge-Elkan算法在以下场景中表现出色：

1. 实体识别与对齐

在知识图谱构建和数据清洗中，用于识别不同数据源中指代同一实体的字符串。例如，将"张三丰"和"张三峰"识别为同一人的不同写法。

1. 地址匹配

在物流、地图服务等场景中，用于匹配存在拼写错误或简写的地址。例如，将"北京市海淀区中关村大街"和"海淀中关村大街"匹配为同一地址。

1. 姓名匹配

在用户注册、身份验证等场景中，用于匹配存在拼写错误或不同写法的姓名。例如，将"李小龙"和"李小龙"匹配为同一人。

1. 机构名称匹配

在学术研究、企业信息整合等场景中，用于匹配不同写法的机构名称。例如，将"北京大学"和"北大"匹配为同一机构。

1. 产品名称匹配

在电商、产品数据库等场景中，用于匹配存在拼写错误或缩写的产品名称。例如，将"苹果iPhone 12 Pro Max"和"苹果12 Pro Max"匹配为同一产品。

六、算法实现与优化

在实际应用中，Monge-Elkan算法可以通过以下方式实现和优化：

实现方式：

• 分词处理：使用合适的分词工具（如中文的jieba分词，英文的nltk分词）对字符串进行预处理。
• 相似度函数选择：根据具体场景选择合适的词级相似度函数，如归一化编辑距离或Jaro-Winkler相似度。
• 动态规划优化：对编辑距离计算使用动态规划技术，提高计算效率。
• 并行计算：对于大规模数据，可以采用并行计算技术加速相似度计算。

优化策略：

• 停用词过滤：在分词后过滤掉无意义的停用词（如"的"、"了"等），减少计算量并提高准确性。
• 长度限制：对过长的字符串进行截断或分段处理，降低计算复杂度。
• 缓存机制：对频繁比较的词对进行缓存，避免重复计算。
• 阈值控制：设置相似度阈值，只保留超过阈值的匹配结果，提高匹配质量。

Python实现示例：

import Levenshtein

def monge_elkan_similarity(s1, s2, tokenization=lambda x: x.split()):
    tokens1 = tokenization(s1)
    tokens2 = tokenization(s2)

    total_similarity = 0.0
    for token1 in tokens1:
        max_token_similarity = 0.0
        for token2 in tokens2:
            edit_distance = Levenshtein距离(token1, token2)
            normalized_distance = edit_distance / max(len(token1), len(token2))
            similarity = 1.0 - normalized_distance
            if similarity > max_token_similarity:
                max_token_similarity = similarity
        total_similarity += max_token_similarity

    return total_similarity / len(tokens1) if tokens1 else 0.0

这个简单的Python实现展示了Monge-Elkan算法的核心逻辑，可以通过替换分词函数和词级相似度函数来适应不同语言和应用场景。

七、总结与应用建议

Monge-Elkan算法通过分词后逐词比较和平均化的方式，提供了一种有效处理复杂字符串相似度的方法。其核心价值在于能够保留字符串的内部结构信息，同时处理局部错误和词序变化，在实体识别、数据清洗等场景中具有广泛应用前景。

在实际应用中，建议注意以下几点：

1. 根据具体语言和应用场景选择合适的分词规则，中文推荐使用最大匹配分词，英文可以使用空格分隔。
2. 根据字符串特点选择合适的词级相似度函数，短字符串（如人名）推荐使用Jaro-Winkler相似度，长字符串推荐使用归一化编辑距离。
3. 对于大规模数据，可以结合其他技术（如停用词过滤、长度限制、并行计算）来提高算法效率。
4. 设置合理的相似度阈值，过滤掉低质量的匹配结果，提高最终匹配的准确性。

通过合理配置参数和优化实现，Monge-Elkan算法可以成为处理复杂字符串相似度的有效工具，在数据清洗、知识图谱构建等场景中发挥重要作用。