基于Q-Grams的文本相似度算法：从日常例子到数学公式

Q-Grams相似度算法是一种简单有效的文本相似度计算方法，通过将字符串分解为连续的q长度子串，再利用集合操作计算相似度。这种方法能够捕捉文本中的局部模式，对拼写错误、短文本匹配等场景表现优异，且计算效率高，适合实时应用。本文将通过通俗易懂的例子、清晰的原理步骤和详细的公式解释，帮助NLP新手全面理解这一算法。

一、Q-Grams概念与生成过程

Q-Grams（也称q-gram或滑动窗口）是一种将字符串分解为固定长度连续子串的技术。假设我们有两个句子：“苹果香蕉橙子"和"苹果橘子西瓜”，我们想比较它们的相似度。首先需要将这两个句子转换成Q-Grams集合。

以q=3为例，生成过程如下：

1. 添加边界符：在句子前后添加特殊符号（如$），确保首尾字符也能参与Q-Grams生成。转换后句子变为：
   1. “苹果香蕉橙子” → “$苹果香蕉橙子$”
   2. “苹果橘子西瓜” → “$苹果橘子西瓜$”
2. 滑动窗口切分：按长度为3的窗口从左到右滑动，每次移动一个字符，记录所有子串：
   1. 第一个句子生成的3-Q-Grams：
   2. [“$苹果”, “苹果香”, “果香蕉”, “香蕉橙”, “橙子$”]第二个句子生成的3-Q-Grams：
3. [“$苹果”, “苹果橘”, “果橘子”, “橘子西”, “子西瓜$”]转换为集合：将这些子串转换为无序的集合形式，便于后续计算：
   1. 集合1：{“$苹果”, “苹果香”, “果香蕉”, “香蕉橙”, “橙子$”}
   2. 集合2：{“$苹果”, “苹果橘”, “果橘子”, “橘子西”, “子西瓜$”}

在这个例子中，两个句子有1个共同的Q-Gram（"苹果"开头的部分），总共有8个不同的Q-Grams。通过这种分解方式，我们能够捕捉到文本中的局部特征，即使整个句子差异较大，也能发现部分相似性。

二、Q-Grams相似度计算实例

现在，我们使用生成的Q-Grams集合来计算两个句子的相似度。计算过程分为三个步骤：

1. 计算交集：找出两个集合中共同的Q-Grams
   1. 集合1 ∩ 集合2 = {“$苹果”}
   2. 交集大小 = 1
2. 计算并集：合并两个集合中的所有Q-Grams
   1. 集合1 ∪ 集合2 = {“$苹果”, “苹果香”, “果香蕉”, “香蕉橙”, “橙子$”, “苹果橘”, “果橘子”, “橘子西”, “子西瓜$”}
   2. 并集大小 = 9
3. 应用公式：使用Jaccard系数公式计算相似度
   1. 相似度 = 交集大小 / 并集大小 = 1/9 ≈ 0.111

这个结果表示两个句子的相似度约为11.1%，说明它们有少量相似的局部特征。如果我们将q值调整为2，重新计算：

• 集合1（q=2）：{“$苹果”, “苹果香”, “果香蕉”, “香蕉橙”, “橙子$”}

→ 实际上，当q=2时，切分结果为：

• [“$苹果”, “苹果香”, “果香蕉”, “香蕉橙”, “橙子$”]（每个子串长度为2）集合2（q=2）：{“$苹果”, “苹果橘”, “果橘子”, “橘子西”, “子西瓜$”}

→ 切分结果为：

[“$苹果”, “苹果橘”, “果橘子”, “橘子西”, “子西瓜$”]此时交集大小仍为1，并集大小为9，相似度不变。但若句子更相似，如"苹果香蕉橙子"和"苹果香蕉橘子"，使用q=3时：

• 集合1：{“$苹果”, “苹果香”, “果香蕉”, “香蕉橙”, “橙子$”}
• 集合2：{“$苹果”, “苹果香”, “果香蕉”, “香蕉橘”, “橘子$”}
• 交集大小 = 3，并集大小 = 7 → 相似度 = 3/7 ≈ 0.429

相似度约为42.9%，明显高于前一对句子，说明这种方法能够有效捕捉文本中的相似模式。

三、Q-Grams相似度算法原理步骤

Q-Grams相似度算法的完整原理步骤如下：

1. 文本预处理
   1. 将文本转换为统一格式（如全小写）
   2. 去除无关字符（如标点符号）
   3. 添加边界符（如在字符串前后添加$）
   4. 示例：原始文本"你好世界" → 预处理后"$你好世界$"
2. 生成Q-Grams
   1. 选择合适的q值（通常为2-4）
   2. 按滑动窗口方式生成所有连续的q长度子串
   3. 示例：q=3时，生成子串列表[“$你好”, “你好世”, “好世界”, “世界$”]
3. 构建特征集合
   1. 将Q-Grams列表转换为集合形式
   2. 集合操作便于后续计算交集和并集
   3. 示例：集合{“$你好”, “你好世”, “好世界”, “世界$”}
4. 计算相似度
   1. 计算两个集合的交集大小
   2. 计算两个集合的并集大小
   3. 应用Jaccard系数公式计算相似度
   4. 示例：集合A和集合B的相似度 = |A ∩ B| / |A ∪ B|

这种方法的核心在于将文本转换为Q-Grams集合，然后利用集合操作计算相似度。通过调整q值，可以控制算法对文本局部特征的关注粒度。q值越大，关注的局部模式越长，但生成的Q-Grams数量越少；q值越小，关注的局部模式越短，但生成的Q-Grams数量越多。

四、Q-Grams相似度数学公式详解

Q-Grams相似度算法主要基于Jaccard系数，其数学公式为：

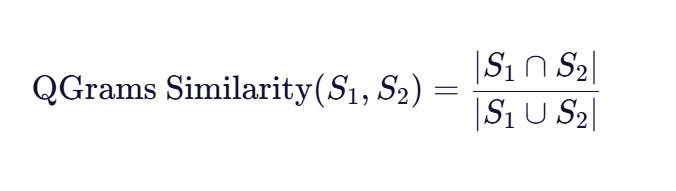公式各部分解释

1. 集合操作

• S1 ∩S2 ：两个Q-Grams集合的交集，表示共同出现的Q-Grams数量
• S1 ∪S2 ：两个Q-Grams集合的并集，表示所有出现的Q-Grams数量
• 示例：若集合A有5个Q-Grams，集合B有7个Q-Grams，它们有2个共同Q-Grams，则：交集大小 = 2，并集大小 = 5 + 7 - 2 = 10

1. Jaccard系数特性

• 取值范围：[0,1]
  • 0表示完全不相似
  • 1表示完全相同
• 无序性：不考虑Q-Grams出现的顺序
• 简单性：计算高效，适合大规模文本比较

1. q值的影响
   1. q值越小（如q=2）：更关注相邻字符的组合，对拼写错误更敏感
   2. q值越大（如q=4）：更关注较长的字符序列，对整体结构更敏感
   3. 实际应用中，q值通常取2-4，具体选择取决于文本长度和应用场景。例如，短文本（如用户名、产品名称）适合较小的q值，而长文本（如文章、评论）适合较大的q值。
2. 边界符的作用
   1. 添加边界符（如$）是为了确保首尾字符也能参与Q-Grams生成
   2. 例如，字符串"苹果"添加边界符后变为"$苹果$"
   3. 生成的Q-Grams（q=2）为[“$苹果”, “苹果$”]
   4. 如果不添加边界符，生成的Q-Grams为[“苹果”]，信息量减少

公式应用示例

以q=3为例，比较两个句子：

句子A：“我爱学习NLP技术”

句子B：“我爱研究机器学习”

1. 预处理并添加边界符：
   1. A：“$我爱学习NLP技术$”
   2. B：“$我爱研究机器学习$”
2. 生成Q-Grams：
   1. A的Q-Grams：[“$我爱学”, “我爱学习”, “爱学习NLP”, “学习NLP技术”, “NLP技术$”]
   2. B的Q-Grams：[“$我爱研”, “我爱研究”, “爱研究机”, “研究机器学习”, “机器学习$”]
3. 计算交集和并集：
   1. 交集：两个集合中没有共同的Q-Grams → |A ∩ B|=0
   2. 并集：两个集合共有10个不同的Q-Grams → |A ∪ B|=10
   3. 相似度：0/10 = 0 → 表示两个句子在q=3级别的局部特征上完全不相似

如果将q值调整为2：

1. 生成Q-Grams：
   1. A的Q-Grams：[“$我爱”, “我爱学”, “爱学习”, “学习NLP”, “NLP技术”, “技术$”]
   2. B的Q-Grams：[“$我爱”, “我爱研”, “爱研究”, “研究机”, “机器学习”, “学习$”]
2. 计算交集和并集：
   1. 交集：{“$我爱”} → |A ∩ B|=1
   2. 并集：共有11个不同的Q-Grams → |A ∪ B|=11
   3. 相似度：1/11 ≈ 0.091 → 相似度仍较低，但比q=3时有所提高

如果两个句子更相似，如：

句子C：“我爱学习NLP技术”

句子D：“我爱学习自然语言处理”

使用q=2计算：

1. Q-Grams交集：{“$我爱”, “我爱学”, “爱学习”, “学习NLP”, “NLP技术”, “技术$”} ∩ {“$我爱”, “我爱学”, “爱学习”, “学习自然”, “然语言处理”, “语言处理$”}
   1. 共同Q-Grams：{“$我爱”, “我爱学”, “爱学习”}
   2. 交集大小 = 3
2. Q-Grams并集大小 = 10（A的6个 + B的5个 - 1个重复）
3. 相似度：3/10 = 0.3 → 表示两个句子有30%的相似局部特征

五、Q-Grams与其他相似度算法的对比

Q-Grams相似度算法与几种常见文本相似度算法的对比如下：

算法名称	基本原理	优点	缺点
Q-Grams相似度	基于Q-Grams集合的Jaccard系数	计算高效，适合短文本，对拼写错误敏感	无法捕捉语义信息，对长文本效果有限
余弦相似度	基于词频向量的夹角余弦	考虑词频信息，适合长文本	计算复杂度高，无法直接处理字符级相似度
编辑距离	计算两个字符串之间转换所需的最小操作数	直接反映字符串差异程度	计算复杂度高（O(nm)），不适合大规模应用
SimHash	生成文本的二进制指纹，比较海明距离	抗噪声能力强，适合去重	特征丢失较多，无法精确反映相似度

Q-Grams相似度算法在计算效率和对局部模式的敏感度方面具有优势，特别适合以下场景：

• 数据清洗：检测重复或相似的文本记录
• 拼写检查：识别相似但存在拼写错误的文本
• 实体链接：匹配不同来源的实体名称
• 短文本相似度：如产品名称、用户名等的相似度计算

然而，它也有明显的局限性：无法捕捉语义信息，对长文本的相似度判断可能不够准确。在实际应用中，通常会结合其他算法（如TF-IDF、余弦相似度）来提高准确性。

六、Q-Grams相似度算法的应用实例

1. 文本去重

在新闻聚合网站中，Q-Grams相似度算法可用于检测相似或重复的新闻文章。例如，比较两篇关于同一事件的文章：

文章A：“北京今日发布最新交通管制政策，全市主干道限行时间为7:00-20:00，周末除外。”

文章B：“北京最新交通管制政策今日生效，全市主要道路限行时间为7:00-20:00，周末不执行。”

使用q=3计算Q-Grams相似度，两个文章的相似度可能达到0.7以上，表明它们内容高度相似，可以合并或标记为重复。

2. 拼写纠错

在搜索引擎中，Q-Grams相似度算法可用于识别用户输入中的拼写错误。例如，用户搜索"苹果手机购买"，但实际想搜索"苹果手机购买"：

正确查询：“苹果手机购买”

错误输入：“苹果手机购买”

计算它们的Q-Grams相似度（q=2），相似度约为0.8，系统可以识别这是一个常见的拼写错误，并推荐正确的查询结果。

3. 用户名匹配

在社交网络中，Q-Grams相似度算法可用于匹配相似用户名，防止用户创建重复或近似账号。例如：

用户名A：“张三123”

用户名B：“张山123”

计算它们的Q-Grams相似度（q=2），相似度约为0.7，系统可以认为这是一个潜在的重复账号，并进行相应的处理。

七、Q-Grams相似度算法的优化方向

尽管Q-Grams相似度算法简单高效，但仍有优化空间：

1. 加权Q-Grams：对不同位置或不同类型的Q-Grams赋予不同权重，例如首尾Q-Grams权重更高，或特殊字符组合权重更高。
2. 动态q值选择：根据文本长度或类型动态调整q值，例如短文本使用较小的q值，长文本使用较大的q值。
3. 与其他算法结合：将Q-Grams相似度与其他算法（如TF-IDF、余弦相似度）结合使用，提高相似度判断的准确性。
4. 索引优化：对于大规模文本集合，可以构建Q-Grams倒排索引，加速相似度计算。

Q-Grams相似度算法虽然简单，但其灵活性和高效性使其在许多实际应用中表现优异。通过调整q值和边界符，可以控制算法对文本局部特征的关注粒度；通过与其他算法结合，可以弥补其无法捕捉语义信息的局限性。作为NLP新手，掌握Q-Grams相似度算法是理解更复杂文本相似度计算方法的基础。