(来自考研真题——原题见2017年的408计组真题)
通过实例理解:
#include<stdio.h>
//f(n)=2^(n+1)-1
int f1(unsigned n){
int sum=1,power=1;
for(unsigned i=0;i<=n-1;i++){
power*=2;
sum+=power;
}
return sum;
}
float f2(unsigned n){
float sum=1,power=1;
for(unsigned i=0;i<=n-1;i++){
power*=2;
sum+=power;
}
return sum;
}
int main(){
unsigned u=0;
printf("%u\n\n", u-1);//u-1的机器数为全一
//注:2^32-1=4294967295
unsigned i=0;
if(i<u-1){
printf("u-1在与无符号数i的比较中被看作无符号数\n\n");
}
printf("f1(23):%d\n",f1(23));
printf("f1(23)十六进制形式:%x\n",f1(23));
printf("f2(23):%f\n",f2(23));//23为使f2(n)的结果精确无舍入的最大n
printf("f1(24):%d\n",f1(24));
printf("f2(24):%f\n\n",f2(24));//采用了末位加1的舍入方法
printf("f1(30):%d\n",f1(30));//f1(30)仍等于f(n)
printf("f1(31):%d\n\n",f1(31));//f1(31)机器数为全1
printf("f2(126):%f\n",f2(126));//126为使f2(n)的结果不溢出的最大n
printf("f2(127):%f\n\n",f2(127));//机器数为7F80 0000H,即无穷大
return 0;
}
输出结果:
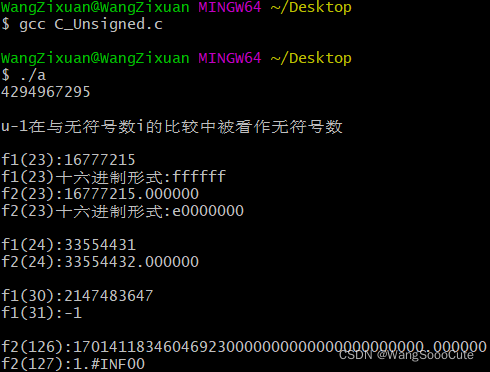





 这篇博客通过示例展示了两个函数f1和f2,分别用于计算2的幂减一,探讨了它们在处理无符号整数23、24和30时的行为,以及当n超出范围时f2的浮点溢出情况。重点在于演示了整数溢出和浮点精度问题在实际编程中的体现。
这篇博客通过示例展示了两个函数f1和f2,分别用于计算2的幂减一,探讨了它们在处理无符号整数23、24和30时的行为,以及当n超出范围时f2的浮点溢出情况。重点在于演示了整数溢出和浮点精度问题在实际编程中的体现。
















 2556
2556

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








