Leetcode每日一题:53.maximum-subarray(最大子序和)

最新推荐文章于 2020-07-02 09:39:07 发布

CodeLuweir

最新推荐文章于 2020-07-02 09:39:07 发布

阅读量319

点赞数

分类专栏： Leetcode 文章标签： leetcode 动态规划

本文链接：https://blog.youkuaiyun.com/wyll19980812/article/details/105899832

版权

Leetcode 专栏收录该内容

169 篇文章

订阅专栏

本文深入探讨了求解最大子数组和问题的多种算法实现，包括非递归、递归及动态规划方法。通过具体代码示例，阐述了每种方法的思路与效率对比，特别强调了非递归实现的时间复杂度优势。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

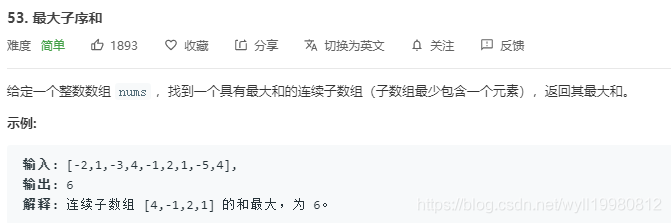
在这里插入图片描述
虽然是简单题，但思路还是挺巧妙地：

非递归实现
假设当前进行到 nums[cur],若前面地和为sum ，执行sum=sum+nums[cur] 小于0，将sum与sunMax比较，然后将sum置0，为什么要置0？因为前面的已经是负数了，-1 + a（a为任何数）肯定是小于a的，所以我们直接从下一个数(cur+1)开始；
如果sum>0，直接与sumMax比较即可；
时间复杂度O（n），空间复杂度常数

递归实现
递归实现比较容易理解，但是效率不及非递归;
f(n)=max(f(n-1)+nums[cur],nums[cur]);
思路是一样的，把nums[cur]加入到前面的和序列中或者不加入(那么新的序列就从cur开始)

动态规划
f(n)=max(f(n-1)+nums[cur],nums[cur]);

C++
非递归实现：
在这里插入图片描述


int maxSubArray(vector<int> &nums)
{
    int len = nums.size();
    if (len == 0)
        return 0;

    int sum = 0, maxSum = nums[0];
    for (int i = 0; i < len; i++)
    {
        sum += nums[i];
        if (sum > maxSum)
            maxSum = sum;
        if (sum < 0)
        {
            sum = 0;
        }
    }
    return maxSum;
}

递归实现
超时

int fun(vector<int> nums, int &sumMax, int cur)
{
    if (cur == -1)
    {
        return 0;
    }
    int sum = max(fun(nums, sumMax, cur - 1) + nums[cur], nums[cur]);
    if (sum > sumMax)
        sumMax = sum;
    return sum;
}

int maxSubArray(vector<int> &nums)
{
    int sumMax = nums[0];

    fun(nums, sumMax, nums.size() - 1);
    return sumMax;
}

动态规划:
在这里插入图片描述

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        int sum = 0, sumMax = nums[0];
        for (int x:nums) {
            sum = max(sum + x, x);
            sumMax = max(sumMax, sum);
        }
        return sumMax;
    }
};