机器学习基础--各种学习方式（13）--降维

降维（Dimensionality Reduction）

　　与聚类方法类似，对数据中的固有结构进行利用，使用无监督的方法学习一种方式，该方式用更少的信息来对数据做归纳和描述。这对于对数据进行可视化或者简化数据很有用，也有去除噪声的影响，经常采用这种方法使得算法更加高效。
　　常规的降维方法：

Principal Component Analysis (PCA)
Partial Least Squares Regression (PLS)
Sammon Mapping
Multidimensional Scaling (MDS)
Projection Pursuit

---

降维的距离

欧式距离降维
曼哈顿距离降维
马氏距离降维

　　另外，在高纬中，任意两个随机高斯向量是正交的。所以高纬的欧式距离会失效。

---

降维方法分为线性的和非线性的两种

　　计算机的图像识别技术是一个异常高维的识别技术。不管图像本身的分辨率如何，其产生的数据经常是多维性的，这给计算机的识别带来了非常大的困难。想让计算机具有高效地识别能力，最直接有效的方法就是降维。

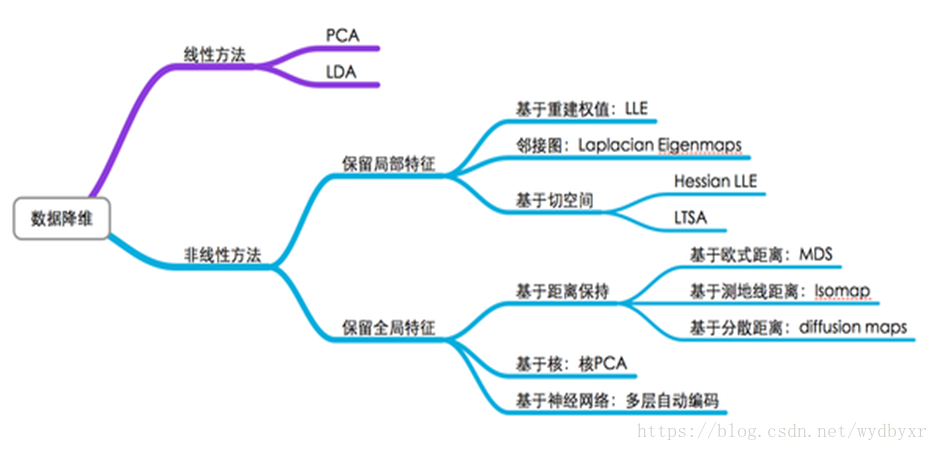
线性的降维方法

　　它们的特点是简单、易于理解。但是通过线性降维处理的是整体的数据集合，所求的是整个数据集合的最优低维投影。
　　常用的方法例如：主成分分析（PCA,Principal Components Analysis）和线性奇异分析（LDA,Linear Discriminant Analysis）等就是常见的线性降维方法。还有MDS(Classical Multidimensional Scaling)。

非线性的降维方法

　　经过验证，线性的降维策略计算复杂度高而且占用相对较多的时间和空间，因此就产生了基于非线性降维的图像识别技术，它是一种极其有效的非线性特征提取方法。
　　此技术可以发现图像的非线性结构而且可以在不破坏其本征结构的基础上对其进行降维，使计算机的图像识别在尽量低的维度上进行，这样就提高了识别速率。
　　非线性降维中用到的方法大多属于流形学习方法。例如人脸图像识别系统所需的维数通常很高，其复杂度之高对计算机来说无疑是巨大的“灾难”。由于在高维度空间中人脸图像的不均匀分布，使得人类可以通过非线性降维技术来得到分布紧凑的人脸图像，从而提高人脸识别技术的高效性。
　　常用的方法例如：等距映射(Isomap,Isometric Mapping)、局部线性嵌入(LLE,Locally Linear Embedding)、拉普拉斯特征映射(LE,Laplacian Eigenmaps) 。

　　不同流行学习算法和可视化算法的比较：
http://scikit-learn.org/stable/auto_examples/manifold/plot_lle_digits.html