《数据流通关键技术》之三：零知识证明.md

知识准备

零知识证明是难啃的骨头，先准备下技术基础：同态加密 看这篇 《数据流通关键技术》之一：同态加密.md

---

多项式盲验

假设你已经理解了同态加密，接下来我们将同态加密应用到多项式盲验中

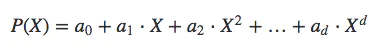
设置如上的多项式，A知道各个系数，但是不想告诉B；B知道X的取值，但是不想告诉A

如果现在要获取多项式加密结果，怎么办？

1. 对s的每个指数，B计算E(1)，E(s)，…，E(sd)，并发送给A

2. A知道多项式的所有系数，可以利用同态特性计算P(s)，并回送给B

这样就达到了我们要的效果，相互不知情，但是可以得出加密后的结果

完整的多项式盲验证

上一章提供的多项式盲验证方式有一个致命的问题，就是B根本没法验证A是真正利用多项式P(s)去计算结果，也就是说无法证明A真正知道这个多项式P(X)。我们继续完善一下上面的验证。

要解决这个问题，我们沿用上面的思路，由B生成一些发给A，而且B可以对A返回的信息进行校验

我们先定义一个概念：α对是指满足b=α*a的一对值（a，b）。注意这里的乘法其实是椭圆曲线（ECC）上的乘法，椭圆曲线上的运算符合两个特性：一是当α值很大的情况下，很难通过a和b倒推出α，二是加法和乘法满足可交换群的特性，也就是说加法和乘法交换律在椭圆曲线上也是成立的。

1. B随机选择一个α生成α对（a，b），α自己保存，（a，b）发送给A
2. A选择γ，生成(a′,b′)=(γ⋅a,γ⋅b)，把(a′,b′)回传给B。利用交换律，可以证明(a′,b′)也是一个α对，b′=γ⋅b=γα⋅a=α(γ⋅a)=α⋅a′
3. B校验(a′,b′)，证实是α对，就可以断言A知道γ

任意计算转换到多项式证明

通过基本的运算符把原计算画成这样的“计算门电路”。

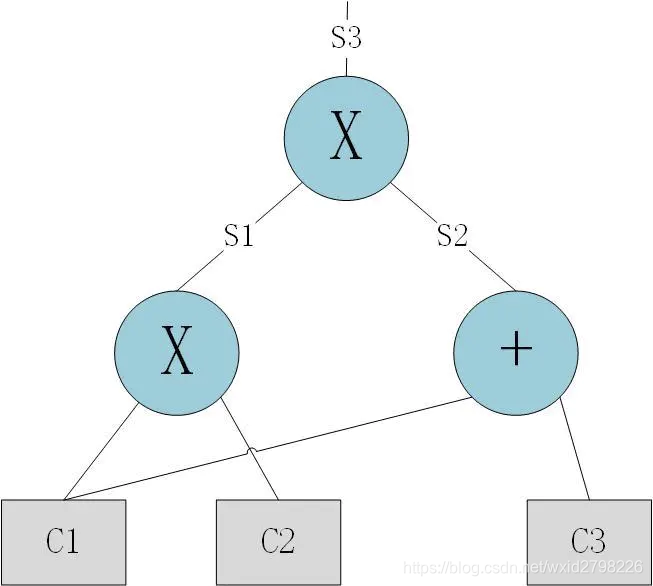
最终我们把原算式的证明转化成为多项式的证明，只要证明P(x)=T(x)*H(x)，即可验证原算式。

存在H（X），使P(x)=T(x)*H(x)，其中T(x)=(x-1)(x-2)(x-3)

---

零知识证明的4大技术基础