基础算法_02_动态规划

最新推荐文章于 2022-04-25 17:09:47 发布

山野村夫_pro

最新推荐文章于 2022-04-25 17:09:47 发布

阅读量263

点赞数

分类专栏：基础算法文章标签：动态规划

本文链接：https://blog.youkuaiyun.com/wwyl1001/article/details/100797613

版权

基础算法专栏收录该内容

5 篇文章

订阅专栏

1. 引入：上台阶问题

入门例子：一个10级的台阶，每次只允许走1个或2个台阶，一共有几种走法？

每一步，上几个台阶，都是一个决策问题。

我们可以试着倒着考虑，最后一次决策，上到第10级台阶是怎么来的？
显然有两种可能：要么是第9级迈1步，要么是第8级迈2步。

记f(n)表示上到第n级台阶的所有走法，则f(10) = f(9) + f(8)，那么f(9) = f(8) + f(7)，f(8) = f(7) + f(6)，......

如果这样自顶向下计算的话，会有两个问题：1. 有很多子问题重复计算了；2. 时间复杂度是 O(n^2)

动态规划采用自底向上的“做备忘录”的方法计算最优结果：

代码如下：

func footStep(step int) int {
    if step <= 0 {
        return 0
    }
    
    if step == 1 {
        return 1
    } 
    
    if step == 2 {
        return 2
    }
    
    prePre := 1
    pre := 2
    result := 0
    for i := 3; i <= step ; i++ {
        result = prePre + pre
        prePre = pre
        pre = result
    }
    
    return result
}

2. 理论基础

动态规划通常应用于最优化问题。
分治算法会将问题划分成一些独立的子问题，递归的求解各子问题，然后合并子问题的解得到原问题的解。
动态规划适用于子问题不是独立的情况，也就是各子问题包含公共的子子问题。动态规划对公共的子子问题只求解一次，将其结果保存起来（做备忘录），从而避免了重复计算。

动态规划的三板斧：
两个特征：1. 最优子结构； 2. 重叠子问题
一个方法：自底向上的做备忘录

2.1 最优子结构

如果问题的一个最优解中包含了子问题的最优解，那么该问题具有最优子结构。当一个问题具有最优子结构时，提示我们动态规划可能适用（贪心算法也可能适用）。在动态规划中，我们利用子问题的最优解来构造原问题的一个最优解，这也是一种自底向上的方式利用最优子结构。

如上台阶问题中，f(10) = f(9) + f(8)，f(10)是上10级台阶的最优解，f(9)和f(8)分别是上9级和上8级的最优解。满足问题的一个最优解包含了子问题的最优解，所以具有最优子结构的。

2.2 重叠子问题

当一个递归算法不断地调用同一个问题时，我们说该最优问题包含重叠子问题。动态规则总是充分利用重叠子问题，即通过每个子问题只解一次，把解保存起来供后续使用。

如上台阶问题中，f(10) = f(9) + f(8)，f(10)和f(9)f(8)是同一个问题。

2.3 自底向上的做备忘录

如上台阶问题中，用pre和prePre把子问题结果保存起来，如果用递归算法求解的话，复杂度高且很多子问题重复计算。

2.4 步骤

1）描述最优解的结构
2）递归定义最优解的值
3）自底向上计算最优解

三、经典例题

3.1 最长公共子序列LCS

若X = {a, b, c, b, d, a, b}，Y = {b, d, c, a, b, a}
那么，{b, c, a}是它们的一个公共子序列（不要求连续），
{b, c, b, a}是它们的一个最长公共子序列LCS，其长度是4，{b, d, a, b}也是它们的一个LCS。

1）最优子结构
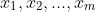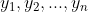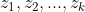设X = { x_1, x_2, ... , x_m }，Y = { y_1, y_2, ... , y_n }，并设 Z_k = { z_1, z_2, ..., z_k }是X和Y的任意一个LCS。
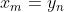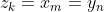如果 x_m = y_n ，那么 z_k = x_m = y_n ，那么 Z_k_-_1 是 X_m_-_1 和 $Y_n_-_1$ 的一个 LCS
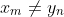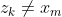如果 $x_m \neq y_n$ ，且 $z_k \neq x_m$ ，那么 Z_k 是 X_m_-_1 和Y的一个LCS
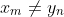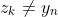如果 $x_m \neq y_n$ ，且 $z_k \neq y_n$ ，那么 Z_k 是和 $Y_n_-_1$ 的一个LCS

上述表明了两个序列的一个LCS也包含了两个序列前缀的一个LCS，这说明LCS具有最优子结构。

2）一个递归解
为了找到X和Y的一个LCS，经上面分析，可能要检查一个或两个子问题
如果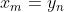 x_m = y_n ，那么要找出 X_m_-_1 和 $Y_n_-_1$ 的一个LCS，然后将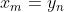添加到这个LCS末尾就可以产生X和Y的一个LCS；
如果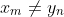 $x_m \neq y_n$ ，就必须解决两个子问题：找出X和 $Y_n_-_1$ 的一个LCS，以及找出 X_m_-_1 和Y的一个LCS。在这两个LCS中，较长的就是X和Y的一个LCS。可以很容易看出LCS具有重叠子问题特征。

记c[i, j]为序列 X_i 和 Y_j 的一个LCS长度。那么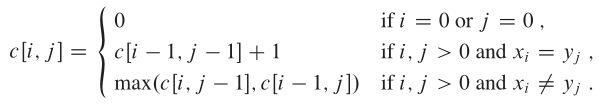

代码如下：

package main
 
import "fmt"
 
func main() {
    X := []string {"A", "B", "C", "B", "D", "A", "B"}
    Y := []string{"B", "D", "C", "A", "B", "A"}
    
   c, b := LCS(X, Y)
   fmt.Println(c)
   fmt.Println(b)
   LSC_Print(b, X, len(X), len(Y))
}
 
func LCS(X,Y []string) ([][]int, [][]string){
     m := len(X)
     n := len(Y)
     
     c := make([][]int, 0) //c[i][j]为Xi与Yi的一个LCS长度
     b := make([][]string, 0)//b[i][j]记录最优解
     //1. 初始化
     for i := 0; i <= m; i++ {
         cc := make([]int, 0)
         bb := make([]string, 0)
         for j := 0; j <= n; j++ {
             cc = append(cc, 0)
             bb = append(bb, "-")
         }
         c = append(c, cc)
         b = append(b, bb)
     }//到此，c[m][n]全是0，b[m][n]全是“-”                                                                                                                                                                    
     
     //2. 自底向上计算
     for  i := 1; i <= m; i++ {
         for j := 1; j <= n; j++ {
             if X[i-1] == Y[j-1] { //xi == yi
                 c[i][j] = c[i-1][j-1] + 1
                 b[i][j] = "ok"
             } else if c[i-1][j] >= c[i][j-1] {
                 c[i][j] = c[i-1][j]
                 b[i][j] = "up"
             } else {
                 c[i][j] = c[i][j-1]
                 b[i][j] = "left"
             }
         }
     }
     
     return c, b
 }
 
 func LSC_Print(b [][]string, X []string, i, j int) {
     if i == 0 || j == 0 {
         return
     }
     
     if b[i][j] == "ok" {
         fmt.Printf("(%d, %d)\n", i,j )
         LSC_Print(b, X, i-1, j-1)
         fmt.Printf("%s ", X[i-1])
     } else if b[i][j] == "up" {
         LSC_Print(b, X, i-1, j)
     } else {
         LSC_Print(b, X, i, j-1)
     }
 }

3.2 背包问题

3.3 最短路径

参考：
1. 漫画：5分钟了解什么是动态规划？
2. 漫画：什么是动态规划？