偏差与方差分解，与过拟合欠拟合的联系？

最近在看机器学习周志华那本书，受益颇多。我们先抛过来几个问题，再一一解答。

• 什么是偏差-方差分解？为什么提出这个概念？

• 什么是偏差？什么是方差？

• 什么是偏差-方差窘境？应对措施？

1、偏差-方差分解的提出

我们知道训练往往是为了得到泛化性能好的模型，前提假设是训练数据集是实际数据的无偏采样估计。但实际上这个假设一般不成立，针对这种情况我们会使用训练集训练，测试集测试其性能，上篇博文有介绍评估策略。对于模型估计出泛化性能，我们还希望了解它为什么具有这样的性能。这里所说的偏差-方差分解就是一种解释模型泛化性能的一种工具。它是对模型的期望泛化错误率进行拆解。

2、偏差-方差分解推导

样本可能出现噪声，使得收集到的数据样本中的有的类别与实际真实类别不相符。对测试样本 x，另 y_d 为 x 在数据集中的标记，y 为真实标记，f(x;D) 为训练集D上学得模型 f 在 x 上的预测输出。接下来以回归任务为例：

模型的期望预测：

 

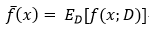
样本数相同的不同训练集产生的方差：

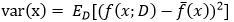
噪声：

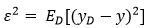
期望输出与真实标记的差别称为偏差：

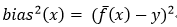
 通过简单的多项式展开与合并，模型期望泛化误差分解如下：

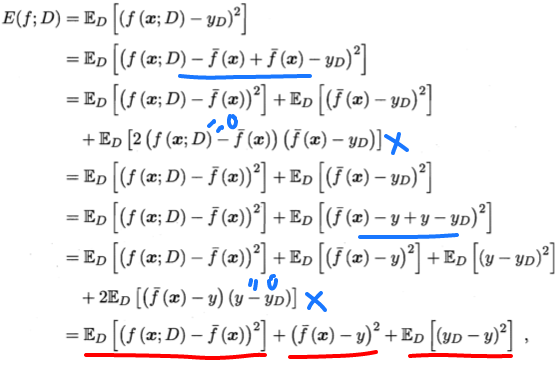
即泛化误差可分解为偏差、方差和噪声之和。

画红线部分是分解后由这三部分方差、偏差、噪声组成。偏差那部分因为和D无关，所以去掉了E_D。画蓝线部分用了数学技巧，并且有两项等于0约简。

3、偏差、方差、噪声

偏差：度量了模型的期望预测和真实结果的偏离程度，刻画了模型本身的拟合能力。

方差：度量了同样大小的训练集的变动所导致的学习性能的变化，即刻画了数据扰动所造成的影响。

噪声：表达了当前任务上任何模型所能达到的期望泛化误差的下界，刻画了学习问题本身的难度。

4、偏差-方差窘境

为了得到泛化性能好的模型，我们需要使偏差较小，即能充分拟合数据，并且使方差小，使数据扰动产生的影响小。但是偏差和方差在一定程度上是有冲突的，这称作为偏差-方差窘境。

下图给出了在模型训练不足时，拟合能力不够强，训练数据的扰动不足以使学习器产生显著变化，此时偏差主导泛化误差，此时称为欠拟合现象。当随着训练程度加深，模型的拟合能力增强，训练数据的扰动慢慢使得方差主导泛化误差。当训练充足时，模型的拟合能力非常强，数据轻微变化都能导致模型发生变化，如果过分学习训练数据的特点，则会发生过拟合。

针对欠拟合，我们提出集成学习的概念并且对于模型可以控制训练程度，比如神经网络加多隐层，或者决策树增加树深。针对过拟合，我们需要降低模型的复杂度，提出了正则化惩罚项。

 

 

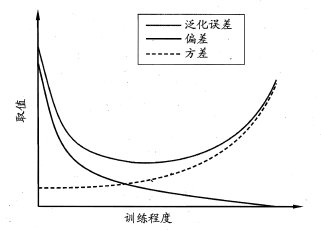
过拟合的高方差是说的预测值的数据集合,

（图中不太明显）
欠拟合–纵轴相对集中
过拟合–纵轴相对分散

作者：优达学城（Udacity）
链接：https://www.zhihu.com/question/27068705/answer/129656963
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

转载优达学城的回答如下：

机器学习讲算法之前，需要先弄懂很多概念，这些概念很多是来自统计学的，这也是为什么传统的机器学习叫做基于统计的机器学习。对这些概念的理解一定要牢，否则就像技术债，它一定会回来咬你让你付出更大的代价。这也是为什么在我们优达学城(Udacity)平台上的机器学习课程中，第一部分不是讲建模，而是先讲模型的评估和验证。(更多关于机器学习相关视频与课程可以查看这里：机器学习工程师（中/英）)

这些概念维基都可以查到，但是没什么用，不如举个例子。

你提到了**准确率Accuracy**：

这也是最基本和最常见的分类指标。准确率是被描述为在特定类的所有项中正确分类或标记的项的数量。举例而言，如果教室里有 15 个男孩和 16 个女孩，人脸识别软件能否正确识别所有男孩和所有女孩？如果此软件能识别 10 个男孩和 8 个女孩，则它的识别准确率就是 60%：

准确率 = 正确识别的实例的数量/所有实例数量

但与人们直觉相反的是，准确率在有些时候并不能说明问题。我们拿京东最近反腐败做例子，假设京东有10000名员工，其中有10个是腐败分子，另外9990是吃瓜群众。某个算法在这10000人中只正确的识别出了1个腐败分子，请问算法的正确率是多少？

中国还有一句老话，叫做宁可错杀一千不可放过一个。意思是宁可误判多一点，也不能把真的漏掉。例如某种癌症筛查，第一步检查尽可能把所有有迹象的都挑出来，让他们去做进一步检查去排除，也不要在第一步就忽略，让患者直接回家。相反，如果你的算法用作犯罪坚定，判定之后就直接死刑执行了，这时可千万不能冤枉任何一个好人。

你提到了Error，我们都不想让模型预测有太多的error，那样就失去了机器学习的意义。但你要知道这些error是怎么来的。

在模型预测中，模型可能出现的误差来自两个主要来源，即：因模型无法表示基本数据的复杂度而造成的偏差（bias），或者因模型对训练它所用的有限数据过度敏感而造成的方差（variance）。我们会对两者进行更详细的探讨。

1. 偏差（bias）造成的误差（error） - 准确率和欠拟合

如前所述，如果模型具有足够的数据，但因不够复杂而无法捕捉基本关系，则会出现偏差。这样一来，模型一直会系统地错误表示数据，从而导致预测准确率降低。这种现象叫做欠拟合（underfitting）。

简单来说，如果模型不适当，就会出现偏差。举个例子：如果对象是按颜色和形状分类的，但模型只能按颜色来区分对象和将对象分类（模型过度简化），因而一直会错误地分类对象。

或者，我们可能有本质上是多项式的连续数据，但模型只能表示线性关系。在此情况下，我们向模型提供多少数据并不重要，因为模型根本无法表示其中的基本关系，我们需要更复杂的模型。那是不是拟合程度越高越好呢？也不是，因为还会有方差。

2. 方差（variance）造成的误差 - 精准度和过拟合

方差就是指模型过于贴近训练数据，以至于没办法把它的结果泛化（generalize）。而泛化是正事机器学习要解决的问题，如果一个模型只能对一组特定的数据有效，换了数据就无效了，我们就说这个模型过拟合。

上面的说法还是太抽象，我们换个比喻。一个学生，根本没学会加减法，你给他再多的题，他也还是不会。训练量的增加对他没有帮助。还有一个学生记忆力特别好，你发现他做练习还不错，但是一到考试就挂。你仔细观察发现，其实他没有学会加减法，而是在做练习的时候偷看答案，他所知道的1+1=2是背下来的，练习中如果没有4-3，你考他它就不会了。

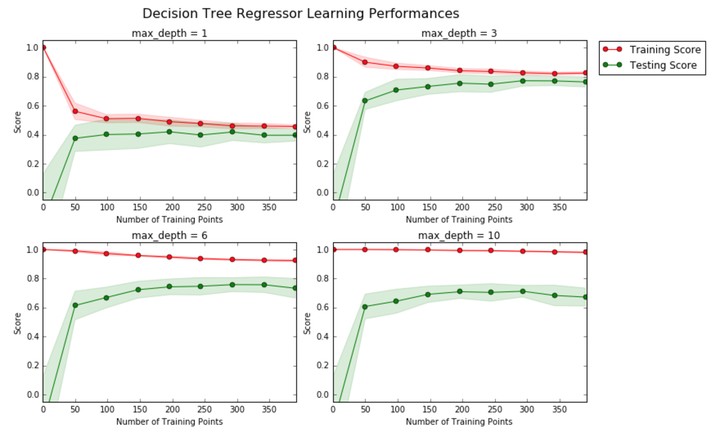
上图中，你能看出来哪个模型偏差（bias）大，哪个模型方差（variance）大，哪个模型是这里面的最优选择吗？

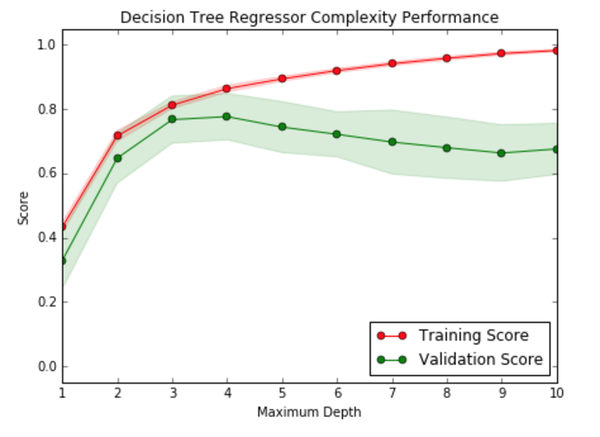
上图是随着模型复杂度增加训练集和验证集的分数。如果你觉得模型的最佳的复杂度应该是几？