本文探讨了机器学习中偏差-方差分解的概念，解释了偏差（预期预测与真实结果的偏离）和方差（数据扰动引起的学习性能变化）如何影响模型的泛化性能。简单模型通常偏差大、方差小，而复杂模型则反之。过拟合和欠拟合分别对应于方差和偏差主导的情况。通过训练集和测试集的表现，可以判断模型是否处于欠拟合或过拟合状态，并据此调整模型复杂度。
对于机器学习算法，可以通过实验估计其泛化性能，但是为什么不同算法在不同训练集上有不同的错误率？欠拟合和过拟合的深层原因到底是什么？“偏差-方差分解”(Bias-Variance decomposition)是解释算法泛化性能的一种常用工具。
顾名思义，偏差-方差分解就是试图把学习算法的期望泛化错误率分解为偏差和方差。偏差指的是期望预测和真实结果之间的偏离程度，而方差指的是因相同数量的训练集的变化而引起的学习性能的变化。
简单的模型拟合能力弱，预测的偏差大，同时受数据扰动小，方差也比较小；复杂的模型拟合能力强，偏差比较小，但是对数据扰动更加敏感，所以方差就比较大。
下面来看具体的例子：
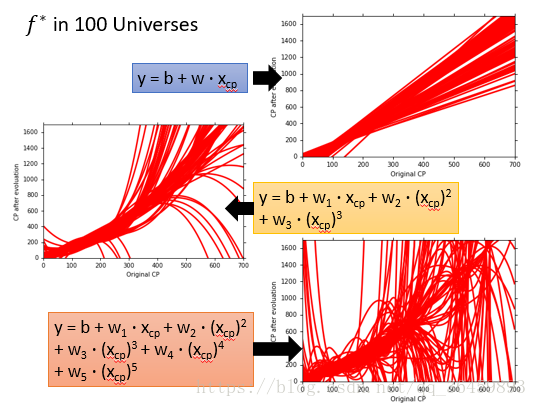
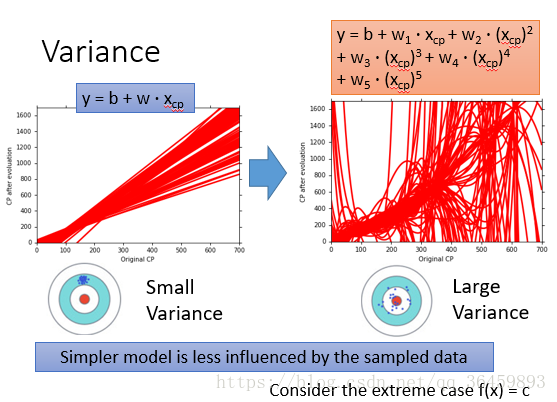
从上面的例子可以看出，模型简单（阶数低）时，拟合的曲线比较接近，但是离“靶心”比较远；模型复杂（阶数高）时，拟合的曲线比较“杂乱”，但是其均值离“靶心”很接近。因此可以直观的看出随着模型复杂度的增加，相同数量下不同训练集的差异（数据扰动）对学习性能的影响越来越大，也即方差Variance越来越大。
下面来看偏差Bias，需要注意的是，偏差指的是学习算法的期望预测和真实结果之间的差异。<
最低0.47元/天 解锁文章
扫一扫
1万+
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
