深度学习记录_深度学习预测保费-优快云博客

本文链接：https://blog.youkuaiyun.com/wslf123/article/details/83868624

本文深入探讨了深度学习的基础概念，包括学习算法定义、过拟合与欠拟合、超参数调整、估计偏差与方差、最大似然估计及贝叶斯统计。同时，文章详细解析了监督学习与无监督学习的原理，以及随机梯度下降在深度学习中的应用。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

这篇博客主要是对《深度学习》这本书的一些记录

第5章机器学习基础

这一章节的主要目录为：学习算法的定义 -- 过拟合和欠拟合 -- 超参数 -- 估计偏差与方差 -- 最大似然估计 -- 贝叶斯统计 -- 监督和无监督学习 -- 随机梯度下降

1. 学习算法的定义，首先得了解3个变量，任务T, 性能度量P 和经验E

任务T包括：分类，输入缺失分类(学习一组函数，每个函数对用有着不同缺失输入子集的x)，回归[设置保险费，预测证券未来的价格]，转录, 机器翻译，结构化输出，异常检测，合成与采样，缺失值填补，去噪，密度估计

性能度量P: 准确率和错误率。经验E: 有监督学习和无监督学习。

2. 容量、过拟合和欠拟合。

欠拟合：模型不能在训练集上获得足够低的误差。

过拟合：训练误差和测试误差之间的差距太大。

容量：指其拟合各种函数的能力。容量低的模型很难拟合训练集，容量高的可能会过拟合。输入改变输入特征的数目和加入这些特征对应的参数，改变模型的容量。

非参数模型：容量任意高的极端情况，如最邻近回归

没有免费午餐定理：没有一个机器学习的方法总是比其他的要好。暗示我们必须在特定任务上设计性能良好的机器学习算法，我们通过建立一组学习算法的偏好来达到这个要求。

正则化：正则化一个学习函数 $f = (x;\Theta )$ 模型，我们可以给代价函数添加被称为正则化的惩罚，在权重衰减的例子中： $J(W) = MSE_{train} + \lambda W^{T} W$ 正则化项是 $\Omega (w) = w^{T}w$ 。在这个例子中，我们明确表示了偏好权重较小的线性函数。有很多其他地方隐式或显示地表示对不同解的偏好，这些方法都被成为正则化。正则化是指修改学习算法，使其降低泛化误差而非训练误差。

3. 超参数与验证集

参数：就是模型可以根据数据可以自动学习出的变量，应该就是参数。比如，深度学习的权重，偏差等

超参数：就是用来确定模型的一些参数，超参数不同，模型是不同的(这个模型不同的意思就是有微小的区别，比如假设都是CNN模型，如果层数不同，模型不一样，虽然都是CNN模型哈。)，超参数一般就是根据经验确定的变量。在深度学习中，超参数有：学习速率，迭代次数，层数，每层神经元的个数等等。
(原文：https://blog.youkuaiyun.com/uestc_c2_403/article/details/77428736)

验证集：用于挑选超参数的数据子集。

4. 估计、偏差和方差

估计：点估计和函数估计

估计的偏差： $bias(\Theta_{m} )=E(\Theta_{m} )-\Theta$ ，其中期望作用在所有数据上，

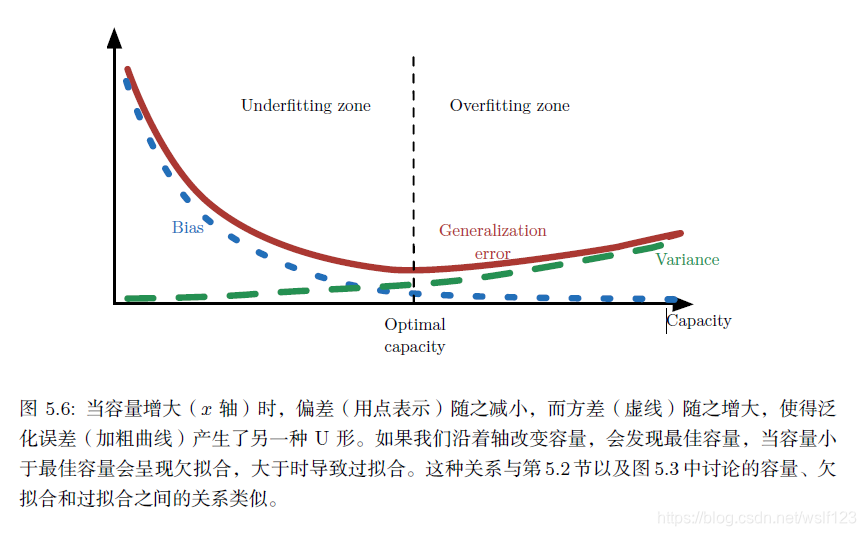
权衡偏差和方差以最小化均方误差：偏差度量着偏离真实函数或者参数的误差期望，而方差度量着数据上任意特定采样的可能导致的估计期望的偏差。

5.最大似然估计：利用已知样本的结果，反推最有可能(最大概率)导致这种结果的参数。

6.贝叶斯统计：

（其实5和6都不怎么会，哈哈）

7.监督学习算法

监督学习是给定一组输入x和输出y的训练集，学习如何关联输入和输出。

概率监督学习：可以使用最大似然估计找到对于有参分布族 $p(y|x;\Theta )$ 最好的参数向量 $\Theta$ 。线性回归中，我们能够通过求解正规方程以找到最佳权重。相比之下，逻辑回归会更困难一些。其最佳权重没有闭解，我们必须通过最大化对数似然来搜索最优解，可以通过梯度下降算法最小化负对数似然来搜索。

支持向量机：类似于逻辑回归，这个模型也是基于线性函数 $w^{T}x+b$ 的,不同的是不输出概率，只输出类别。当结果为正时，支持向量机的预测是正类，反之，为负类。支持向量机一个重要创新是核技巧。

$f(x) = b + \sum_{i}\alpha _{i}k(x,x^{(i)})$ ，其中 $\alpha$ 是系数变量， $k(x,x^{(i)})$ 是核函数，这个函数关于x是非线性的，但是关于 $\Phi (x)$ 是线性的。

核技巧十分强大有两个原因：其一，它使我们能够使用保证有效收敛的凸优化技术来学习非线性模型。第二核函数的实现方法通常比直接构造 $\Phi (x)$ 再算点积高效很多。最常用的核函数是高斯核。

8.无监督学习：

主成分分析：PCA学习一种比原始输入维度更低的表示。

k均值聚类：

9.随机梯度下降：

机器学习算法中的代价函数通常可以分解成每个样本的代价函数的总和，随机梯度下降的核心是，梯度是期望。期望可使用小规模的样本近似估计。具体而言，在算法的每一步，我们从训练集中均匀抽出一小批量（minibatch）样本小批量的数目通常是一个相对较小的数，从一到几百。重要的是，当训练集大小m 增长时，通常是固定的。我们可能在拟合几十亿的样本时，每次更新计算只用到几百个样本。

梯度下降往往被认为很慢或不可靠。以前，将梯度下降应用到非凸优化问题被认为很鲁莽或没有原则。优化算法不一定能保证在合理的时间内达到一个局部最小值，但它通常能及时地找到代价函数一个很小的值，并且是有用的。

随机梯度下降在深度学习之外有很多重要的应用。它是在大规模数据上训练大型线性模型的主要方法。对于固定大小的模型，每一步随机梯度下降更新的计算量不取决于训练集的大小m。在实践中，当训练集大小增长时，我们通常会使用一个更大的模型，但这并非是必须的。达到收敛所需的更新次数通常会随训练集规模增大而增加。然而，当m 趋向于无穷大时，该模型最终会在随机梯度下降抽样完训练集上的所有样本之前收敛到可能的最优测试误差。继续增加m 不会延长达到模型可能的最优测试误差的时间。从这点来看，我们可以认为用SGD训练模型的渐近代价是关于m 的函数的O(1) 级别。