论文阅读-《在直接光源计算和环境映射中结合相关和重要性采样》

一 摘要

本文提出了一种通用的方差减少方法：相关采样和重要性采样的准最优组合。组合的权重是自动选择的，以保持重要性和相关采样的优点，所提出的采样方法用于大面积光源的高效直接光源计算和环境地图反射照明的计算。（PS。是否可用于虚拟平面光源的照射）。

• 如果源是隐藏的，在这些情况下重要性采样会很好
• 而如果源是完全可见的，则相关采样是有效的。所提出的方法自动检测特定情况并提供继承两种技术优点的结果。

二 内容

1.摘要：

• 渲染渲染使用了BRDF，通过计算光路贡献度来进行光线计算。积分应用蒙特卡洛或准蒙特卡洛积分。
• 相关采样：一种方差减少技术，它对蒙特卡洛估计的额外函数施加了不太严格的约束。重要性采样相比，这个要求更容易满足。与重要性抽样不同，相关抽样在计算机图形学中很少受到关注。

2.多重相关抽样：

• 在论文的摘要部分讨论了两种方差减少技术，重要性抽样和相关抽样。将这两种采样方案以保留优势的方式组合在一起。

3.具有相关采样的直接光源计算：

• 假设由于面光源的照射，我们需要在点 ~x 和方向上的反射辐射 Lr。根据渲染方程，辐射度可以得到如下积分
  
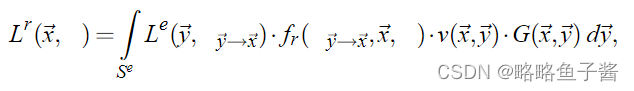
  其中 Se 是光源上的点集，Le(… ) 是点 ~y 向点 ~x 发射的辐射率，fr 是 BRDF，v 是可见度函数如果两个点相互可见，则为 1，否则为零，G 为几何因子。在几何因子中_x,y 是表面法线与连接~x 和~y 的方向之间的角度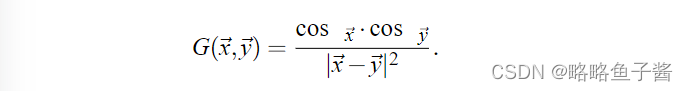

  
  
  这个积分是通过提出的多重相关采样来评估的。使用前面部分的符号，被积点 ~x 和方向的被积函数如下：
  
  为了允许相关采样的应用，让我们找到一个被积函数的近似值，它是解析可积的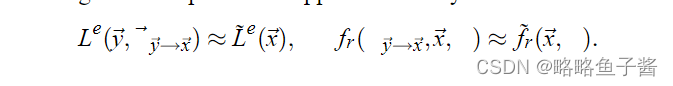
  请注意，如果光源既不是很镜面也不是很大，并且表面不是很亮，这些近似值可能非常准确。
  几何因子的面积积分可以转换为应用斯托克定理的轮廓积分，或者可以应用更简单的几何参数来获得封闭形式的解 。结果在辐射度文献中被称为点到多边形形状因子。
  
  注意：

  • angle(_a,b) 是两个向量之间的有符号角度。如果〜b从〜a顺时针旋转到〜N〜x的相反方向，则符号为正
  • ⊕ 表示以 L 为模的加法（顶点的循环下一个运算符）
  • L是光源多边形的顶点数
  • Rl 是从~x 到光源多边形的第 l 个顶点的向量

• 如果光源完全可见并且光和接收器表面都是漫反射的，则主要部分等于被积函数，因此在这种情况下，相关采样会给出准确的结果。然而，对于部分或完全被遮挡的光源，主要部分可能远离原始被积函数。事实上，对于完全遮挡的光源，经典重要性采样提供了精确的结果，等于零。这意味着相关采样对于完全可见的光源是最佳的，而重要性采样对于完全遮挡的光源是最佳的。在部分遮挡的情况下，我们的偏好应该取决于遮挡的程度。从等式 3 计算的权重反映了这种直觉。为了设置权重，我们可以根据等式 4 定义的可用样本来近似等式 3 的预期值。或者，我们可以采取更激进的方法，使能见度等于分数，即光线的分数每总光线数可见。我们实施了这两种方法并得出结论，第一种方法提供了更好的结果。

• 光源采样的仿真结果（直接光源计算和环境映射中的相关和重要性采样）：
  
  图 4 和图 5 将经典光源采样和纯相关采样与所提出的组合方法进行了比较。当权重被统计计算并且被设置为分数可见性时，组合方法生成视觉上相似的图像。场景由覆盖房间左墙的大光源照亮。我们在每个像素的光源上获得了 10 个随机样本。第一行和第二行分别包含完整图像和放大图像。

4.具有相关采样的天光照明和环境映射：

• 当虚拟物体被真实的天空模型照亮时或者当这些物体应该放置在真实场景中时，来自天空或真实环境的光照通常由定义的环境贴图表示高动态范围图像。虚拟物体的点~x的辐射度是环境贴图提供的光照的反射，可以计算为
  
  

• 方向域的分解：为了分解方向域，可以用球坐标表示方向，使用 = (cos·sin ,sin·sin ,cos ),并且它们的域被分解为间隔 0,1,…,n 和 0,1,…,m。对应于 d = (i,i+1)×(j ,j+1) i 的球域大小