关于平方损失函数和y关于x的线性回归，如何理解给定的x观测到特定y的似然P(y|x)

平方损失与线性回归的似然关系

原创已于 2025-10-18 12:00:35 修改 · 435 阅读

9 ·

CC 4.0 BY-SA版权

文章标签：

#线性回归 #python #机器学习

于 2025-10-18 07:31:46 首次发布

第一部分：先要理解什么是最大似然估计(MLE)

一、核心思想：一句话概括

最大似然估计的核心思想是：在已经得到观测结果的前提下，寻找最有可能（概率最大）导致这个结果的参数值。

把它想象成“侦探破案”：

发生了案件（观测到的数据）。
你有几个嫌疑犯（不同的模型参数）。
最大似然估计就是找出哪个嫌疑犯最有可能犯下这个案件。

二、从一个简单的例子入手：抛硬币

假设你有一枚硬币，你怀疑它可能不均匀（不是公平的硬币）。你想估计这枚硬币抛出正面的概率，我们把这个概率记为 p。

1. 进行实验，收集数据
你抛了这枚硬币10次，结果是：正、反、正、正、正、反、正、正、正、正。
用数据表示就是：[1, 0, 1, 1, 1, 0, 1, 1, 1, 1] (1代表正面，0代表反面)。
在这个数据中，有 8次正面，2次反面。

2. 直觉告诉你什么？
你的直觉可能会告诉你：“既然10次里抛出了8次正面，那正面朝上的概率 p 大概是 8/10 = 0.8。”
你的这个直觉，其实就是最大似然估计的结果！ 现在，我们来看看背后的数学原理是如何支持你这个直觉的。

三、似然函数 (Likelihood Function) - 关键的一步

1. 定义模型
单次抛硬币是一个伯努利试验，其概率为：

P(正面)=p
P(反面)=1−p

2. 计算得到当前观测结果的概率（联合概率）
我们得到的数据是独立的（每次抛硬币互不影响），所以整个序列的概率是每次概率的乘积。

对于一次正面，概率是 p
对于一次反面，概率是 1−p

所以，得到 [1, 0, 1, 1, 1, 0, 1, 1, 1, 1] 这个特定序列的概率是：
L=p×(1−p)×p×p×p×(1−p)×p×p×p×p

我们可以简化一下。因为有8次正面，2次反面，所以：

L(p)= $p^{8}\times (1-p)^{2}$

这个函数 L(p)就叫做似然函数 (Likelihood Function)。

3. 理解“似然”的含义

概率：在已知参数 p (比如 p=0.5) 时，预测可能观测到的结果。
似然：在已知观测结果 (8正2反) 时，去评估不同的参数 p 取值的“合理性”或“可能性”。

所以，似然函数是关于参数 p的函数。我们的目标是找到一个 p 的值，使得这个似然函数 L(p)的值最大。

四、最大化似然函数

我们的任务是：找到哪一个 p 能让 L(p)= $p^{8}\times (1-p)^{2}$ 的值最大。

1. 数学方法（求导）
为了找到最大值，我们通常对似然函数取对数（变成对数似然函数），因为乘积取对数会变成求和，更容易求导，而且对数函数是单调的，不会改变最大值点的位置。

Bingo！ 数学计算告诉我们，当 p=0.8时，似然函数取得最大值。这完美地验证了我们之前的直觉！

五、总结与推广

1. 最大似然估计的通用步骤：

写出似然函数：基于你的数据和模型，写出观测到当前数据的概率表达式 L(θ)，其中 θ 是你要估计的参数。
取对数（通常这样做）：得到对数似然函数 l(θ)=ln⁡L(θ)。
对参数求导：令导数等于零 dl(θ)/dθ=0。
解方程：求出能使似然函数最大的参数值 $\widehat{\theta }$ 。这个 $\widehat{\theta }$ 就是参数 θ 的最大似然估计值。

2. 核心要点：

“似然”不是“概率”：似然描述的是参数的可靠性，而不是未来事件的概率。
MLE是一种思想：它不依赖于具体的分布，无论是正态分布、泊松分布还是其他任何分布，你都可以用这个“找最可能原因”的思想去估计参数。
广泛应用：MLE是现代统计学和机器学习的基石。逻辑回归、高斯混合模型、乃至大型神经网络的训练，其背后都有MLE思想的影子（虽然具体优化算法不同）。

希望这个解释能对最大似然估计有一个清晰而深刻的理解！它其实就是把我们自然的“猜一下”的想法，用严谨的数学工具实现了出来。

第二部分：再理解什么是高斯噪声假设下的线性回归的概率分布

这触及了线性回归的概率解释和频率学派与贝叶斯学派连接的核心。下面一步步来解析。

一、基本设定：线性回归模型

首先，我们有一个线性回归模型：

y= $w^{T}$ x+ϵ

其中：

w 是权重参数
ϵ 是噪声项，通常假设 ϵ~N(0, $\sigma ^{2}$ )

二、从概率角度理解

1. 条件分布

由于 y= $w^{T}$ x+ϵ，且 ϵ 服从正态分布，那么：

y∣x ~ N( $w^{T}$ x, $\sigma ^{2}$ )

这意味着：在给定 x 的条件下，y 服从均值为 $w^{T}$ x、方差为 $\sigma ^{2}$ 的正态分布。

2. 条件概率密度函数

因此，给定 x 观测到特定 y 的概率密度为：

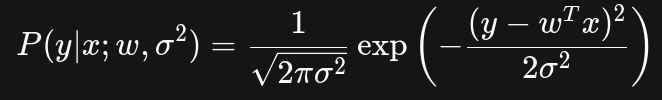
$P\left ( y | x; w^{T}x, \sigma ^{2}\right )= \frac{1}{\sqrt{2\pi}\sigma e^{\frac{(y-w^{T}x)^{2}}{2\sigma ^{2}}}}$

注意：这是概率密度，不是概率（因为 y 是连续变量）。

三、与平方损失函数的联系

1. 最大似然估计的角度

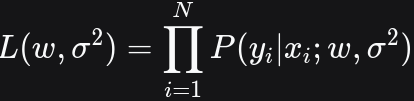
假设我们有 N 个独立同分布的观测数据 $\left \{ (x_{1},y_{1}), (x_{2},y_{2}),... (x_{i},y_{i}),...(x_{N},y_{N}) \right \}$ ，那么似然函数为：

$L\left ( w, \sigma ^{2} \right )=\prod_{i=1}^{N}P\left ( y_{i}|x_{i};w,\sigma ^{2} \right )$

取对数：

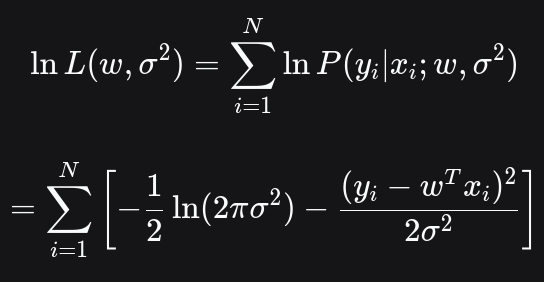
$\ln L\left ( w, \sigma ^{2} \right )=\ln \prod_{i=1}^{N}P\left ( y_{i}|x_{i};w,\sigma ^{2} \right )=-\sum_{i=1}^{N}\left [ \frac{1}{2}\ln \left ( 2\pi \right )+\ln \sigma + \frac{(y_{i}-w^{T}x_{i})^{2}}{2\sigma ^{2}}\right ]$

取最小化负对数似然

$-\ln L\left ( w, \sigma ^{2} \right ) =\frac{N}{2}\ln \left ( 2\pi \right )+N\ln \sigma+\sum_{i=1}^{N} \frac{(y_{i}-w^{T}x_{i})^{2}}{2\sigma ^{2}}$

2. 关键洞察

最大化似然函数或最小化负对数似然函数等价于最小化平方损失函数：

对于固定的标准差 σ，最大化 $\ln L$ 或最小化 $-\ln L$ 等价于最小化：
$\sum_{i=1}^{N} \frac{(y_{i}-w^{T}x_{i})^{2}}{2\sigma ^{2}}=\frac{N}{\sigma ^{2}}\frac{1}{N}\sum_{i=1}^{N} \frac{1}{2}(y_{i}-w^{T}x_{i})^{2}$

这正是我们熟悉的平方损失函数！

重点：最大似然估计值（w, b）就是我们要求解的最佳模型参数

四、深入理解

1. 概率解释

平方损失函数隐含地假设了噪声服从高斯分布
每个观测值 y 在给定 x 的条件下，围绕预测值 wTx呈正态分布
残差 y−wTx反映了噪声的 realization

总结

核心思想：

平方损失函数 ⇔ 高斯噪声假设
P(y|x) 描述了在给定 x 时 y 的不确定性
最小二乘法是高斯噪声假设下的最大似然估计

这种概率视角的优点是：

提供了不确定性量化
允许模型检验和诊断
为贝叶斯方法奠定基础
理解模型假设的局限性

这就解释了为什么"给定 x 观测到特定 y 的似然"与平方损失函数如此紧密相关——它们本质上是同一硬币的两面：一个是概率表述，另一个是优化表述。