忆阻CNN用于轨迹识别
摘要
本文描述了采用忆阻器单元的卷积神经网络在简单运动识别中的应用。卷积神经网络的每个单元包含输入和输出模板,并连接至电压控制忆阻器。实验结果通过仿真软件获得。所提出的模型被证明能够在二维网格上识别简单的像素轨迹。
关键词 ——卷积神经网络;忆阻器;轨迹识别
一、引言
忆阻型细胞神经网络(CNN)在研究论文中被广泛讨论,例如[1, 2, 3]。本研究的目标是探索忆阻系统滞回动力学在运动目标识别或手势识别中的应用。这是对[4]中描述工作的延续。我们提出了一个简化系统模型:一个大小为 7x7的细胞神经网络[5],其包含忆阻单元,用于识别单个黑像素的预定义移动。细胞神经网络被定义为由局部互连的单元组成的网格,整个网络的参数值被称为克隆模板。克隆模板的设计旨在提取图像的特定特征,例如轮廓、边缘、去噪等。
在图像中检测移动物体需要使用带有时间延迟的克隆模板的卷积神经网络[5,6,12]。因此,用于手势识别的忆阻CNN更适合此任务[7]。
基于忆阻器的轨迹识别系统设计包括以下步骤:
- 由阈值电压VT和分段线性模型的两个斜率Į与ȕ定义的忆阻器特性在图2中的选择。
- 卷积神经网络克隆模板A和B的设计,用于处理相邻输入和输出。
我们展示了对选定运动进行仿真的结果,并定义了信号/运动参数和忆阻器特性的一些约束条件。我们设计的系统用于检测时间间隔从0.5秒到数秒范围内的事件。忆阻器的特性决定了系统能够检测到的事件的时间尺度。
我们的运动识别方法的新颖之处在于直接利用忆阻器动力学,将其定义为对外部脉冲的响应方式,该响应受物理定律支配。
本文展示了四个实验的结果——其中三个涉及移动像素(选择一个方向由忆阻CNN进行识别),第四个实验包含一条静态黑像素线,以检查忆阻CNN是否能够区分运动与静态模式。
II. 忆阻器单元模型
所提出的模型由一个相同的忆阻器单元的二维网格组成。采用了一个分段线性存储变阻器模型描述 [5,8,9],其遵循伯努利动力学 [10]。在仿真中使用的电压控制的存储变阻系统的响应由方程(1)-(3)描述。
$$ I(t) = G(x,V_M,t)V_M(t) \tag{1} $$
$$ G = x^{-1} \tag{2} $$
$$ \dot{x} = (\beta V_M + 0.5(\alpha - \beta)[|V_M + V_T| - |V_M - V_T|]) \times \theta(x - R_1)\theta(R_2 - x) \tag{3} $$
忆阻器上的电流和施加的电压分别用 $I(t)$ 和 $V_M(t)$ 表示。$\alpha$ 是系统电阻变化率,当 $|V_M| \leq |V_T|$ 时。$\beta$ 是系统电阻变化率,当 $|V_M| > |V_T|$ 时。R1, R2 是忆阻器的电阻的极限值。阈值电压用 $V_T$ 表示。$\theta(\cdot)$ 表示阶跃函数。
Į、ȕ、R1, R2以及VT的值是通过实验选定的。表 I显示了所有进行的实验中使用的参数值。
| 参数 | 选定值 |
|---|---|
| Į | 0.1 |
| ȕ | 0.212 |
| R1 | 20 |
| R2 | 10000 |
| VT | 15 |
所选忆阻器模型的特性可用分段线性函数 $f(V_M) = \dot{x}$ 表示,如图1所示。

如果 $|V_M| \leq |V_T|$,则 $f(V_M)$ 的斜率是 Į;如果 $|V_M| > |V_T|$,则 $f(V_M)$ 的斜率是 ȕ。忆阻器的电阻 R 在两个有限值 R1 和 R2 之间变化。
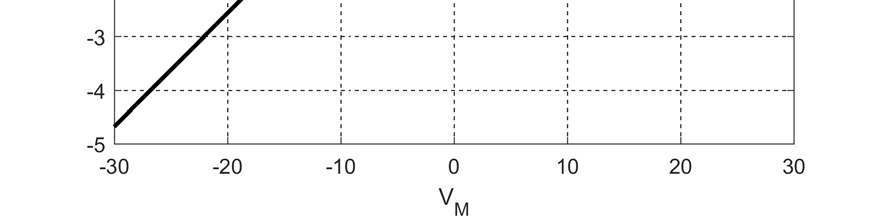
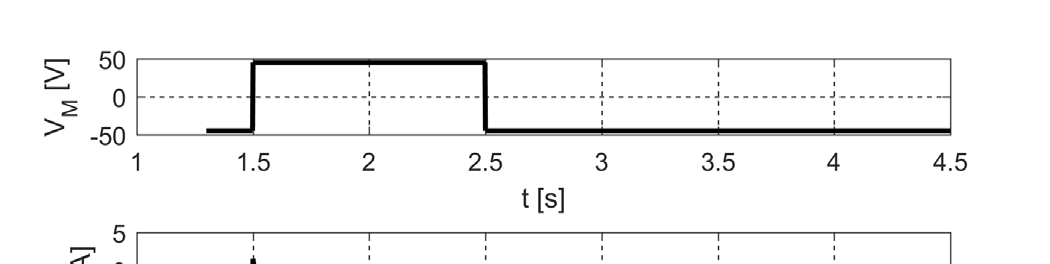
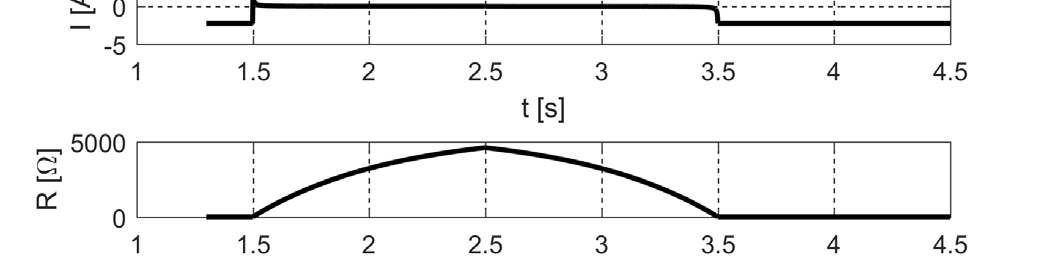
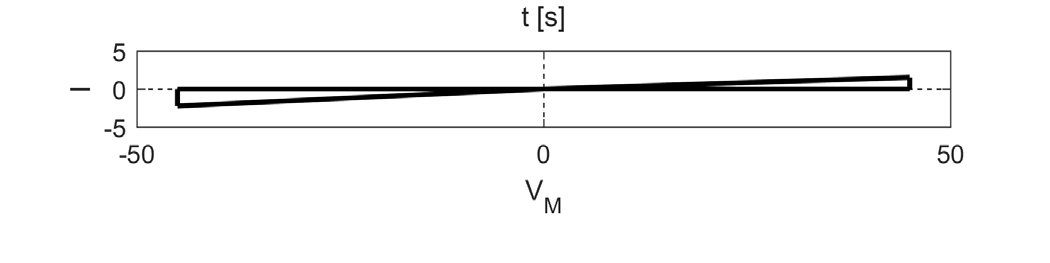
图2 显示了忆阻器特性,包括输入电压 VM (在 t=1.5 s 时从负电压变为正电压,在 t=2.5 s 时方向相反)、输出电流 I、忆阻器的电阻 R 以及电压-电流曲线中的滞回环。VM 波形类似于下一节中描述的忆阻CNN输入端的波形。I 图显示了输出电流。矩形波的持续时间是输入端的两倍。第三张图显示了忆阻器的电阻(最小值为 20 Ω),最后一张图展示了电流-电压图上的滞回环。
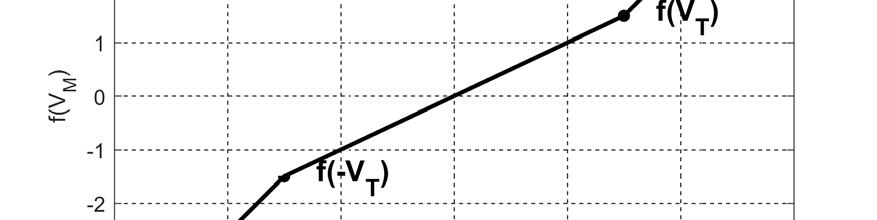
III. 具有忆阻单元的卷积神经网络
忆阻CNN是由相同单元组成的网格。每个输入像素对应一个处理单元。每个单元包含忆阻元件,该元件连接到尺寸为3x3的输入和输出模板,用于计算9个输入和9个输出的加权和。单个CNN单元的结构如图3所示。
卷积神经网络更新规则可以描述为
$$
v_{ij}(t+1) = \sum_{(k,l) \in N_{ij}} a_{kl} x_{ij}(t) + \sum_{(k,l) \in N_{ij}} b_{kl} y_{ij}(t)
\tag{4}
$$
$$
y_{ij}(t+1) = M(v_{ij}(t+1))
$$
其中:
- $a_{ij}, b_{ij}$ — 输入和输出模板分量,
- $x$ — 外部输入(像素值),
- $y$ — 单元输出,
- $v$ — 忆阻元件输入,
- $M()$ — 由公式(1)-(3)描述的忆阻元件执行的函数。
实验在由7x7单元组成的网格上进行。每个单元对应一个像素。当单元与激活单元相连时,输入值设为+1,否则设为-1。像素移动通过在一段时间内将选定的单元设为 +1,然后清除并设置下一个单元来模拟。
模板被选择用于识别像素从网格的左侧到右侧的移动。模板值的选择方法与[11]中描述的方法类似。具体数值通过实验精细调整。所选的模板值为:
$$
A = \begin{bmatrix}
0.1 & -0.1 & 0.1 \
-30 & 30 & -0.1 \
0.1 & -0.1 & 0.1 \
\end{bmatrix}
\tag{5}
$$
$$
B = \begin{bmatrix}
0.1 & -0.1 & 0.1 \
-0.1 & 1 & -0.1 \
0.1 & -0.1 & 0.1 \
\end{bmatrix}
$$
当前方法与先前在[4]中描述的方法之间的主要区别在于增加了模板B以及通过检查是否超过阈值来执行运动识别。
IV. 结果
A. 区分运动与背景
在该实验中,使用了包含7个像素的轨迹,这些轨迹方向不同,并放置在输入网格的不同位置。结果表明,对于所有未直接呈现移动像素的处理单元(即其对应的中心像素从未被设置),它们的输出接近于零。
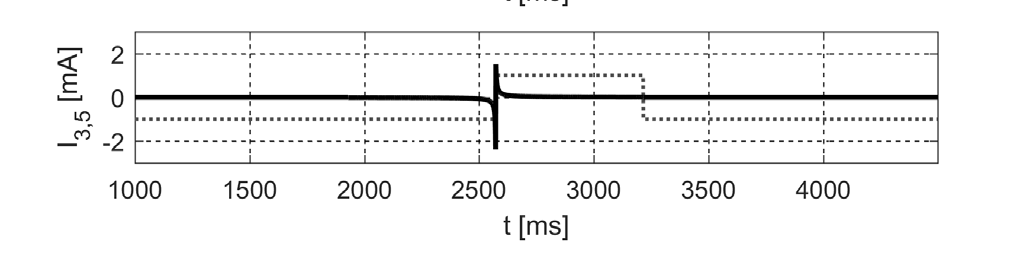
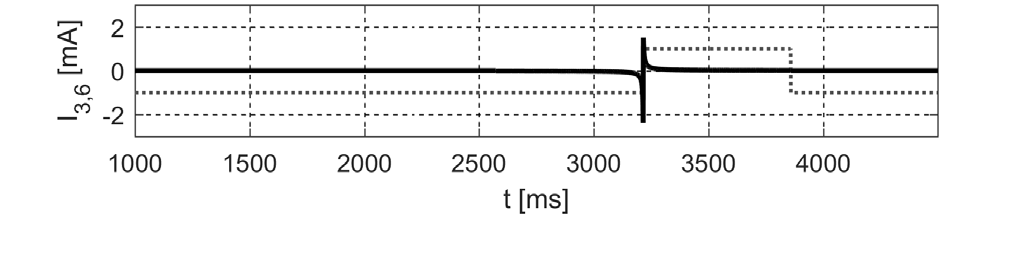
另一方面,所有在网格中从左到右呈现移动像素的单元(图4),其输出模式均与图5所示相似。图中显示了三个位于移动像素下方的细胞的输出情况。虚线灰线表示给定细胞在被模板处理前的输入信号。输出以实心黑线绘制。
细胞(3,4)的激活发生在t=1926到t=2568,细胞(3,5)发生在t=2569到t=3210,第三个细胞(3,6)发生在t=3211到t=3852。当像素受到刺激(变黑)时,可观察到特征性的输出模式,从而实现对运动的识别。
为了检查是否可以区分运动方向,进行了图6和图8所示的实验。在第二次实验中,像素以与第一次实验相同的速度从网格的右侧移动到左侧——从单元格(3,7)移动到单元格(3,1)。第三次实验涉及像素从网格顶部到底部的移动——从单元格(1,4)移动到单元格(1,7)。输出值接近零,证实可以区分运动方向。
 、(3,5)、(3,6)的输出的时序图。实心黑线 – 单元输出,虚线灰线 – 输入信号(模板处理前))
、(3,5)、(3,6)的输出的时序图。实心黑线 – 单元输出,虚线灰线 – 输入信号(模板处理前))
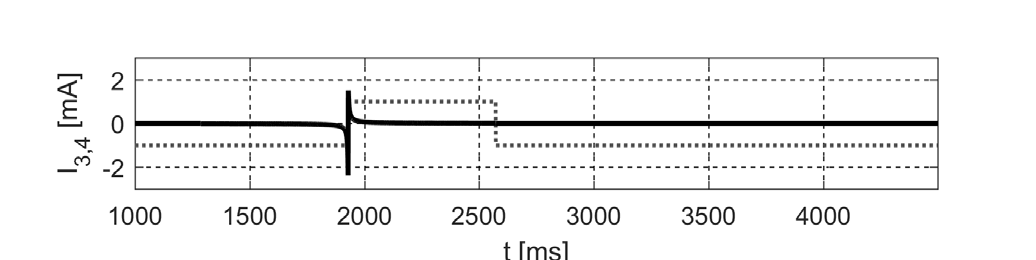 、(3,5)、(3,6)的输出的时序图。实心黑线 – 单元输出,虚线灰线 – 输入信号(模板处理前))
、(3,5)、(3,6)的输出的时序图。实心黑线 – 单元输出,虚线灰线 – 输入信号(模板处理前))
 、(4,4)、(5,4)的输出的时序图。实心黑线 – 单元输出,虚线灰线 – 输入信号(模板处理前))
、(4,4)、(5,4)的输出的时序图。实心黑线 – 单元输出,虚线灰线 – 输入信号(模板处理前))
B. 区分运动与静态图像
在本实验中,将一条包含7个开启(黑色)像素的静态线呈现给模型(图10),持续时间与实验1-3中的动态轨迹相同。
结果(图11)显示,该图像具有与动态轨迹不同的特征。单元格(3,1) - (3,7)的输出接近零,证实输入中不存在移动像素。
我们之前的模型[4]存在一个局限性,即在识别物体运动后,忆阻层和最大池化层都需要重置到初始状态,才能正确检测后续的物体。本文所述的方法不需要这一后处理阶段。
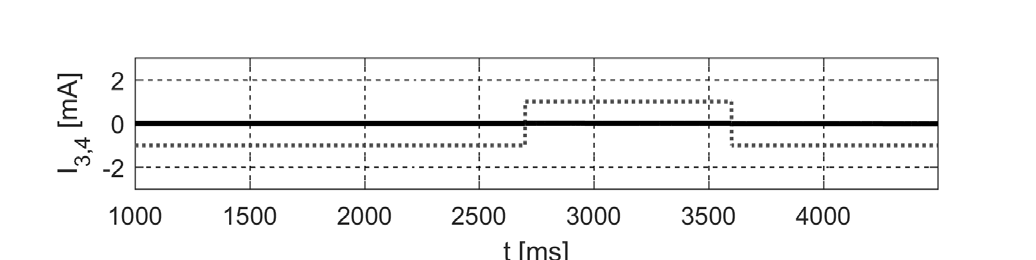
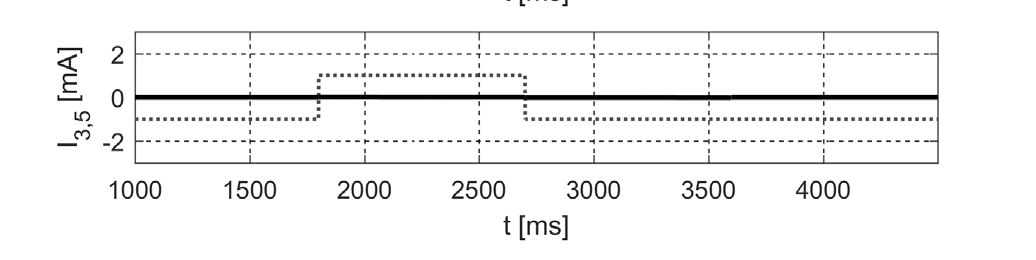 、(3,5)、(3,6)的输出时序图。实心黑线 – 单元输出,虚线灰线 – 输入信号(模板处理前))
、(3,5)、(3,6)的输出时序图。实心黑线 – 单元输出,虚线灰线 – 输入信号(模板处理前))
五、结论
我们展示了具有忆阻细胞的卷积神经网络识别选定运动的能力——一种手势的简单模型。
运动识别的机制通过忆阻单元的非线性动力学实现——其状态演化所体现的记忆效应,类似于时间延迟连接的作用。
成功的手势识别需要根据忆阻器特性参数将像素速度限制在有限区间内。
通过使用严格设计的克隆模板的大规模卷积神经网络,可以将所提出的思想推广到更大范围的手势识别。
我们试图继续开展研究,以展望用于手势识别的纳米尺度系统。





















 5万+
5万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








