[leetcode][DP] 动态规划总结

当优化问题可分为多个子问题，子问题相互关联，子问题的解被重复使用时，考虑使用动态规划求解。

    使用动态规划的条件包括以下两点

1. 优化子结构：问题的和优化解包含子问题优化解，通过求解子问题使得我们可以自上而下的完成求解过程。
2. 重叠子问题：在问题的求解过程中，很多子问题的解将被多次使用。通常将子问题优化解代价保存下来，逐步构造最优解。

    求解动态规划问题，最最重要的是找到递归表达式

64.最小路径和

给定一个包含非负整数的 m x n 网格，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

说明：每次只能向下或者向右移动一步。

输入:
[
  [1,3,1],
  [1,5,1],
  [4,2,1]
]
输出: 7
解释: 因为路径 1→3→1→1→1 的总和最小。

定义数组dp，dp[i][j]代表从位置i,j开始到右下角的最小路径和。

dp[i][j] = Math.min(dp[i][j+1],dp[i+1][j]) + grid[i][j];   取向下和向右移动后的最小路径和的最小值，加上当前代价。

class Solution {
    public int minPathSum(int[][] grid) {
        int m = grid.length;
        int n = grid[0].length;
        int[][] dp = new int[m][n];
        dp[m-1][n-1] = grid[m-1][n-1];
        for (int i=m-2;i>=0;i--) {
            dp[i][n-1] = dp[i+1][n-1] + grid[i][n-1];
        }
        for (int i=n-2;i>=0;i--) {
            dp[m-1][i] = dp[m-1][i+1] + grid[m-1][i];
        }
        for (int i=m-2;i>=0;i--) {
            for (int j=n-2;j>=0;j--) {
                dp[i][j] = Math.min(dp[i][j+1],dp[i+1][j]) + grid[i][j];
            }
        }
        return dp[0][0];
    }
}

322.零钱兑换

给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额，返回 -1。

输入: coins = [1, 2, 5], amount = 11
输出: 3 
解释: 11 = 5 + 5 + 1

输入: coins = [2], amount = 3
输出: -1
说明:
你可以认为每种硬币的数量是无限的。

使用递归的方法在递归树中找到需要最少硬币的方案需要很多重复计算，当硬币面额为[1,2,3]，总金额为6时，递归树如下：

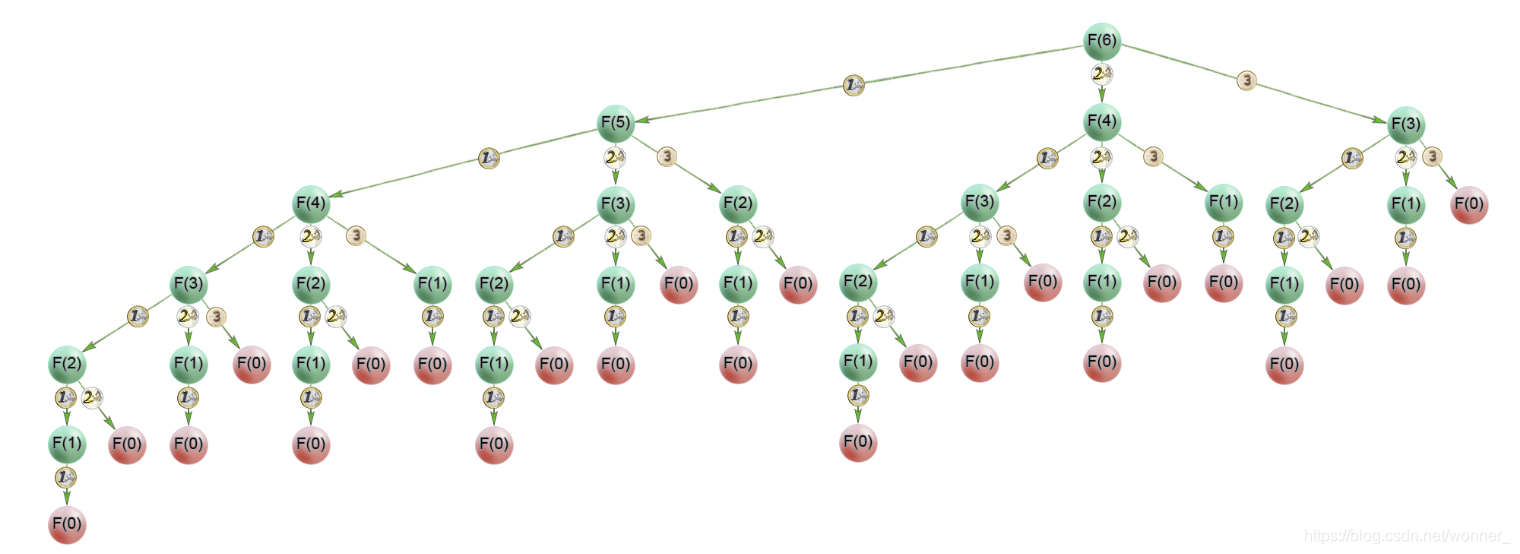
所以采用自底向上的动态规划，定义数组dp，dp[i]代表总金额为i时所需的最少硬币个数。

dp[i]=min{dp[i-coin]+1 for coin in coins} 

class Solution {
    public int coinChange(int[] coins, int amount) {
        int[] dp = new int[amount+1];
        for (int i = 1;i<=amount;i++) {
            int min = Integer.MAX_VALUE;
            for(int coin:coins) {
                if (i-coin>=0 && dp[i-coin]!=-1) {
                    min = Math.min(min,dp[i-coin]+1);
                }
            }
            if (min == Integer.MAX_VALUE) {
                dp[i] = -1;
            } else {
                dp[i] = min;
            }
        }
        return dp[amount];
    }
}

518.零钱兑